采用幾何法直接計算濕球溫度的研究

巫黎明

(江蘇省電力設計院，江蘇 南京 211102)

1 概述

濕球溫度：溫度計的感溫球與空氣直接接觸所測出的空氣溫度稱為空氣的干球溫度，如果用帶有水分的濕紗布包在溫度計的感溫球上，這樣的溫度計就叫濕球溫度計，所測出的溫度就叫濕球溫度，是紗布中的水與周圍空氣進行熱、濕交換達到最終穩定狀態時的溫度。

氣象站觀測濕球溫度主要是為了查算水汽壓與相對濕度兩個氣象要素，自從江蘇省氣象部門在2002～2004年逐步完成建立自動觀測站后，水汽壓與相對濕度兩個氣象要素都能自動觀測了，所以氣象部門就不再觀測濕球溫度了。據了解，其他省份也是如此。

為了給火力發電廠冷卻塔設計提供10%的濕球溫度及相應氣象條件，《電力工程氣象勘測技術規程》DL/T 5158—2002中4.2.1規定：“近期連續不少于5年最炎熱時期(3個月計)頻率為10%的日平均濕球溫度，……，其相應的日平均干球溫度、相對濕度、風速、氣壓應選取10%的日平均濕球溫度出現日的對應值。”從規定可以看出，10%的濕球溫度實際上是為冷卻塔水溫計算確定標準，如果標準定高了，會造成冷卻塔偏大，浪費錢財；如果標準定低了，那么在高溫季節可能造成冷卻水溫過高而報警停機或降低機組出率的嚴重后果。因此10%的濕球溫度計算非常重要。

由于氣象部門在2004年以后就不再觀測濕球溫度這一氣象要素，發電廠冷卻塔參數10%濕球溫度將難以直接計算，為了解決這個問題，《電力工程氣象勘測技術規程》DL/T 5158—2010修訂版征求意見稿4.3節提出了如下濕球溫度計算公式：

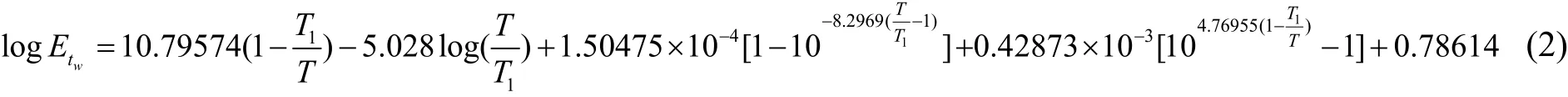
式中：tw為濕球溫度，℃；td為干球溫度，℃；Etw為濕球溫度tw所對應的純水平液面飽和水汽壓，hPa；e為水汽壓，hPa；A為干濕表系數，查表取值，℃-1；Ph為本站氣壓，hPa；T為絕對濕度，為濕球溫度tw加上273.15，K；T1為水的三相點溫度，273.16K。

條文說明4.3.2中：“……。以土耳其某電廠為例，比較2002年～2006年熱季實測濕球溫度和反查《濕度查算表》、差值法、相關法得到的濕球溫度，93%的數據以查表法的偏差最小，最小偏差為0℃，最大偏差為0.7℃，平均偏差為0.3℃，較其它方法為佳。本條文推薦的方法即為查表法的計算公式。”

根據條文說明可以知道，目前對公式還不能直接求解，只能通過查表法、差值法、相關法來近似求解，由于這些方法效率低、易出錯，且精度不高，一直以來困擾著設計工作者。近年來，也有人研究采用迭代法近似求解，但操作也比較繁瑣。

2011年10月出版發行的《電力工程水文氣象計算手冊》8.5.3.3條也沒有對“缺乏實測濕球溫度”提出簡單可行的計算方法。

由于濕球溫度計算數據多，計算工作量大，如何簡單求解以上公式？如何為發電工程水文氣象行業計算累積頻率10%濕球溫度的確定提供論據并節約工時？帶著這個問題，本人經過研究，做出了一套簡單易行的計算方法，對于5年的資料，利用計算機編程，1秒左右就能完成計算；也可以在Excel中直接計算，非常方便。

2 公式的幾何圖形轉換

將公式(1)改變為：

將式(3)兩邊取對數，得下式：

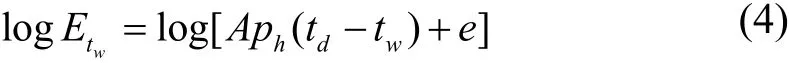
由于td、e、ph、A為已知，求tw，將式(2)、(4)組成一對方程組，由于兩個方程中均隱含tw的未知變量，且不能直接求解。但如果假設一個tw值，就可以根據方程(2)、(4)分別計算出兩個不等的logEtw值，當計算的兩個logEtw值相等時，對應假設的tw值就是要求解的值。

為了便于說明，令y=logEtw、x = tw，將方程(2)、(4)進一步轉化為：

采用南京氣象站1999年8月17日一組實測資料(td=28.5℃ e=29.8hPa ph=1006.7hPa A=0.0007947℃-1)，因為同時觀測的濕球溫度總是低于干球溫度，所以x值從28.5起算，步長取0.2，計算到-0.1，其對應的f1(x)、f2(x)復制到autoCAD中繪制成圖，為了便于表達，將圖局部放大成圖1所示。從圖1中可以看出，y=f1(x)、y= f2(x)是兩條相交的近似直線。假設在x軸上x1處作垂直于x軸的直線分別與兩條近似直線交叉于C、A兩點，在 x2處作垂直于x軸的直線分別與兩條近似直線交叉于G 、E兩點；假設兩條近似直線的交點為D，過D點作一條平行于x軸的直線分別與直線AC交于B點、與直線EG交于F點。再假設各點的坐標值分別為：C(x1，y11)、A(x1，y12)、D(x，y)、B(x1，y)、E(x2，y21)、F(x2，y)、G(x2，y22)。以下采用兩種方法來進一步求解。

圖1 y= f1(x)、y= f2(x)折線圖

2.1 直接計算法

從圖1、圖2可以看出，方程組(5)是兩條交叉近似直線，兩條近似直線的交點(x,y)就是要求解的點，求解的x值就是tw。根據幾何學相似三角形原理：三角形ABD與三角形DFG相似、三角形BCD與三角形DEF相似，根據相似三角形對應邊長成比例的定義有：

據此可以列出如下對應的坐標數值方程組(6)：

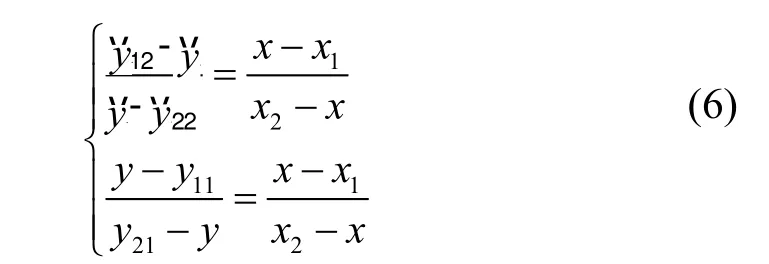
根據方程組(5)可以求解出：

式(7)是以x1小于x、x2大于x推導的。同理，在保證式(6)的幾何意義不變的情況下，x1、x2都小于x或x1、x2都大于x時式(7)均不變。

因為觀測站當日實測的干球溫度總是比濕球溫度高，根據多站資料分析，逐日平均干球溫度與濕球溫度的差值在江蘇省為0.2～6.5，差值的高限在南方可能偏小、在北方偏大。計算時取x2=td，x1取值范圍在td-2與td-8之間都可以，x1分別取td-2、td-8所計算x值的絕對誤差在0.02以內，對結果基本沒有影響。

通過多站資料分析對比，取x1= td-3誤差相對最小，也就是在差值0.2～6.5的中間值附近誤差最小。因此在江蘇省采用x2=td，x1= td-3來計算y21、y22、y11、y12的值，然后計算出x值、也就是求解的tw值。

對于濕球溫度晝夜變化較大的北方地區，y=f2(x)曲率偏大，計算誤差可能達到0.5℃左右，為了解決這一問題，可以縮小范圍進行二次計算：令xx2=x(x為第一次計算值)，xx1=x-0.3再次代入(2)、(4)、(7)式計算，其精度即可達到0.02℃。

據此編程計算，根據連續5年夏季三個月逐日實測的td、e、ph參數來計算逐日平均濕球溫度在1秒左右就可以完成，計算的精度達到0.02℃以內。也可以將式(2)、(4)、(7)編寫到Excel電子表格中直接計算，非常方便。

2.2 迭代法

從圖2可以看出，對應x1可以計算出Δ1=abs(y11-y12)、x2可以計算出Δ2=abs(y21-y22)，abs代表絕對值函數。當Δ趨近于0時所對應的x值就是要求的值，由于兩條近似直線只有一個交點，因此迭代逐步收斂。這里介紹一種變步長迭代法，為了簡單易懂，采用basic語言來表達：

采用以上迭代計算，其初值x與步長st的取值決定迭代步數，如果初值取干球溫度td、步長取5，20步以內完成計算。為了減少迭代步數，初值取td-3，步長取0.5，7～15步以內完成計算。初值的取值理由同前，目的主要是使初值盡量靠近真值，然后按照差值Δ逐漸變小的方向以每步縮減二分之一步長逼近真值。據此編程，計算連續5年夏季三個月逐日平均濕球溫度在2秒左右完成。根據50行Δ1﹤0.0001結束計算條件設置，濕球溫度的計算精度達到0.002℃。

由于該迭代法逐步收斂，只要初值x取值不大于干球溫度且步長取值適當，迭代均可很快完成。但如果x初值大于干球溫度，并使式(3)中[Aph(td- tw)+e]≤0，則程序出錯。

3 誤差的分析

3.1 直接計算與迭代計算誤差的分析

迭代法從理論上來說計算精度最高，其計算誤差小于0.0001。為了檢驗直接計算法的精度，本次采用江蘇省13個氣象站共計806組資料、對直接計算法與迭代法進行比較，以兩種方法計算結果的差值絕對值來統計，結果為：平均差值在0.01℃左右，其中≤0.02℃的個數占85%，≤0.03℃的個數占96%，差值最大為0.06℃的僅有2個，差值為0.05℃的也僅有2個，差值為0.04℃的只有5個。說明兩種計算方法的結果基本接近，滿足濕球溫度計算精度0.1℃要求。

另外，在新疆天山鋁業電廠設計中，采用石河子氣象站2005～2009年夏季6、7、8月共460組資料計算中，直接計算法與迭代法誤差均小于0.03，完全滿足設計要求。

3.2 計算值與觀測值誤差分析

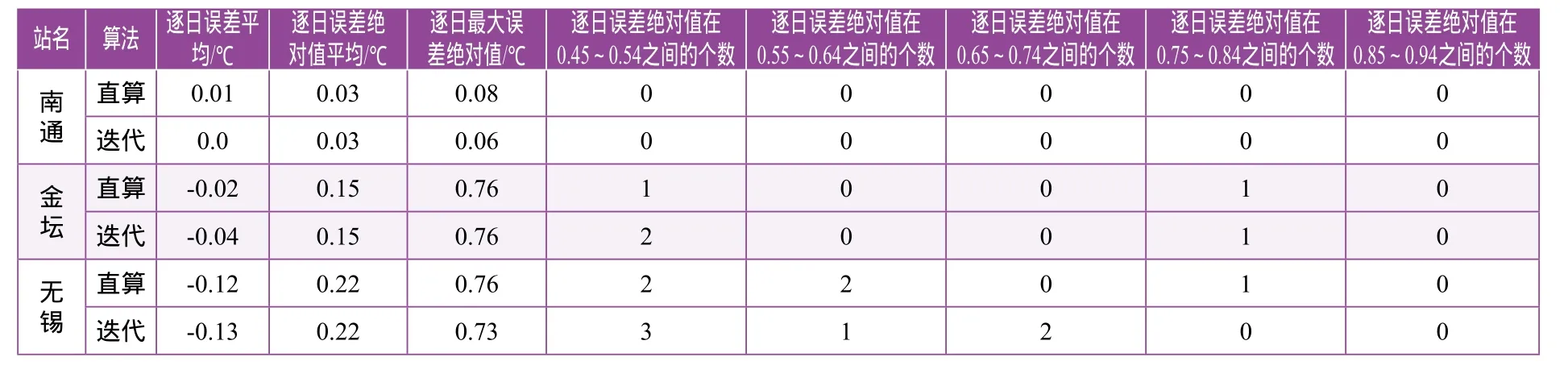
按照地域分布均勻的原則，在江蘇省選用13個氣象站，采用以上直接計算法、迭代法兩種方法，選用2000年7、8兩個月62個實測的逐日平均td、e、ph參數來計算逐日平均濕球溫度，并將逐日計算值減去逐日實測值，對差值進行統計、對比分析，其結果見表3。

表3 逐日平均濕球溫度計算值與實測值統計

(續)

從表3可以看出，本次共分析了13個氣象站共806組資料，其中有8個站逐日誤差絕對值平均數較大，平均誤差在0.15～0.23℃，鹽城氣象站與無錫氣象站為0.22～0.23℃；鹽城、如東、鎮江、無錫4個站出現偏差，計算值比觀測值偏小-0.11～ -0.21℃，其中鹽城站偏小值-0.21℃；逐日誤差絕對值有8個站大于0.5℃，但誤差大于0.7℃的個數只有7個，其中最大值發生在宿遷，為0.87℃。

根據江蘇省氣候中心介紹，南京站、淮安站、南通站、徐州站是每小時觀測一組數據，各要素的日平均值是24次觀測值的平均值，所以代表性高，與公式符合性好；鹽城站、無錫站為3次觀測，日平均值是3次觀測值的平均值，所以代表性就低，易產生偏差；其余站均為4次觀測，代表性介于兩者之間。

由于公式(1)、(2)是根據逐時觀測資料建立的，當采用日平均值來計算時，采用3、次4次觀測值來計算日平均值本身就存在偏差，因此采用公式計算時就會產生偏差，而采用24次觀測值來計算日平均值時基本不存在偏差。

4 結語

本次研究的創新點主要是巧妙地將一組復雜的隱性方程組化解為一組近似線性方程組，并以幾何學中的相似三角形原理來直接求解，解決了濕球溫度求解的難題，使濕球溫度的計算方法變得簡單易懂。

從應用角度來看，直接計算法是對求解濕球溫度這一復雜方程組的重大突破，在確保滿足計算精度的情況下，計算步驟大大減少、計算過程簡單，計算速度可以提高30倍以上，并可以在Excel電子表格中直接計算，滿足批量數據計算，能更好的應用于工程設計，節約工時。

迭代法是傳統求解隱性方程組的方法，屬于試算法，本次經過線性處理后的迭代更簡單明了。

[1]編寫組.國家氣象局.濕度查算表[M].北京：氣象出版社，1986.