中國與美國輸電線路原狀土基礎設計方法對比

劉萬群，曾根生

(廣東省電力設計研究院，廣東 廣州 510663)

1 概述

隨著輸電線路電壓等級和輸送容量的提高，輸電塔基礎力越來越大，如何合理的選用經(jīng)濟適用的基礎型式，以及按原計算方法是否合理值得深入研究。掏挖基礎、挖孔樁基礎是在輸電線路中應用最為廣泛的基礎型式，具有經(jīng)濟、環(huán)保的優(yōu)點。而掏挖基礎和帶擴大頭的挖孔樁基礎外形近似，但計算模型完全不同，當基礎力較大、基礎埋深較深時，如何合理的選擇計算模型是設計人員應當關注的問題，美國標準中此類基礎統(tǒng)稱為“Drilled shaft foundation”，在IEEE Std 691-2001中有比較詳細的介紹，并進行了大量的試驗驗證，值得借鑒。下文對中國的掏挖基礎、帶擴大頭的挖孔樁基礎和美國Drilled shaft基礎的設計方法進行介紹和對比，為輸電工程設計人員提供參考。

2 基本公式

2.1 中國規(guī)范掏挖基礎設計方法

2.2.1 上拔承載力

掏挖基礎上拔穩(wěn)定一般采用剪切法，按下式計算：

當ht≤hc時

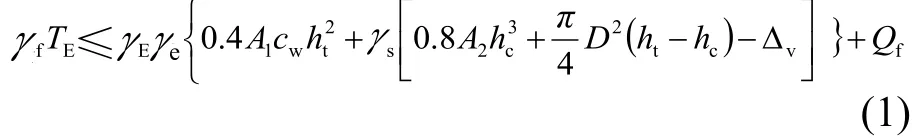
當ht＞hc時

式中：γf為基礎附加分項系數(shù)。直線桿塔取1.1，懸垂轉(zhuǎn)角塔取1.3，轉(zhuǎn)角、終端、大跨越塔取1.6；TE為基礎上拔力設計值；γE為水平力影響系數(shù)；A1、A2為無因次系數(shù)；ht為基礎的埋置深度；γs為基礎底面以上土的加權(quán)平均重度；D為圓形底板直徑；ΔV為(ht-hc)范圍內(nèi)的基礎體積；hc為基礎上拔臨界深度；Qf為基礎自重力；γθ為基底展開角影響系數(shù)，當坡角θ0>45度時取1.2，否則取1.0；cw為計算凝聚力；c為按飽和不排水剪或相當于飽和不排水剪方法確定的凝聚力；Sr為地基土的實際飽和度。

2.1.2 下壓承載力

當軸心荷載作用時：

當偏心荷載作用時：

式中：P為基礎底面處的平均壓力設計值；fa修正后的地基承載力特征值；γef為地基承載力調(diào)整系數(shù)；Pmax為基礎底面邊緣最大壓力設計值。

另外，底板在下壓荷載作用時，其基底壓力不得大于表1。

表1 基底壓力限值

底板剪切承載力應滿足下式要求：

式中：V為計算截面上的剪力設計值；hx為計算截面高度。

2.2 中國規(guī)范挖孔樁基礎設計方法

由以上計算方法可以看出，美國沒有土體剪切模型的計算方法，而是推薦采用圓柱體剪切模型，此計算方法與我國的挖孔樁基礎類似，以下是我國的挖孔樁計算方法。

2.2.1 下壓樁基礎的承載力計算

當根據(jù)土的物理指標與承載力參數(shù)之間的經(jīng)驗關系確定單樁下壓極限承載力標準值時，單樁下壓極限承載力宜按下式計算：

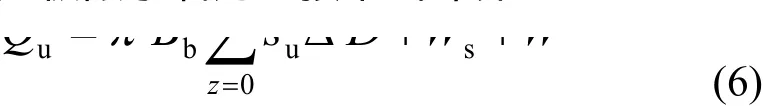
式中：qsik、qpk為第i層土的極限側(cè)阻力標準值和極限端阻力標準值；u為樁的截面周長。

2.2.2 上拔樁基礎的承載力計算

單樁的上拔極限承載力標準值可按下式計算：

式中：Uk為單樁的上拔極限承載力標準值；Gp為單樁(土)或基樁(土)自重設計值，地下水位以下取浮重度，對于擴底樁應按下表確定樁、土柱體周長，計算樁、土自重設計值。

表2 擴底樁、土柱體周長

單樁、群樁基礎及其基樁的上拔極限承載力標準值應按下列規(guī)定確定：

(1)對于一級桿塔樁基，有條件時單樁或基樁的上拔極限承載力標準值應通過現(xiàn)場單樁上拔靜載荷試驗確定。

(2)對于二、三級桿塔樁基。如無當?shù)亟?jīng)驗時，單樁的上拔極限承載力標準值可按下式計算：

式中：γi為抗拔系數(shù)。

2.3 美國規(guī)范Drilled shaft基礎設計方法

Drilled shaft基礎施工流程為：掏挖一個圓形基坑，放置鋼筋籠和地腳螺栓或插入角鋼，澆筑混凝土。圓形基坑的直徑在0.6m～3.0m之間變化，埋深在3m～23m之間變化，如需要人工掏挖時建議最小直徑為0.8m。施工方法取決于地質(zhì)情況和施工單位，當?shù)刭|(zhì)條件比較好時基坑開挖不需要設置支撐，當?shù)刭|(zhì)條件較差時基坑開挖需要套管或泥漿護壁以維持基坑穩(wěn)定。高地下水位的無粘性土或砂土一般都需要開挖支護。因為施工細節(jié)對掏挖基礎承載力影響較大，所以應詳細評估地質(zhì)情況與施工方法的關系，并在基礎設計時考慮這一要素。圖1為Drilled shaft基礎示意圖。

圖1 Drilled shaft基礎示意圖

2.3.1 上拔承載力計算

上拔力作用下的承載力主要為基礎自重和基礎底面與側(cè)面抗力之和，常有的上拔承載力計算模型主要有斜截錐模型、傳統(tǒng)圓柱體剪切模型和摩擦圓柱體法，這三種方法都是建立在一系列直掏挖基礎足尺試驗的基礎上的。

⑴ 斜截錐模型

圖2為斜截錐模型示意圖。其上拔承載力含基礎自重和錐體內(nèi)土的重量兩項，當基礎位于地下水位以下時需要用有效重度來考慮基礎和土的重量，不考慮基底吸力。對于均質(zhì)土，極限上拔承載力Qu可按下式計算：

圖2 斜截錐模型示意圖

⑵ 傳統(tǒng)圓柱體剪切模型

對于直掏挖基礎，模型假定破壞面為基礎與土的接觸面，對于擴底掏挖基礎，模型假定破壞面

為基礎與土的接觸面或以擴底為直徑的圓柱面，見圖3。

圖3 圓柱體剪切模型示意圖

① 直掏挖基礎

不排水剪地基土其上拔承載力含基礎自重和基礎側(cè)面抗力Qsu兩項，不考慮基底吸力。對于均質(zhì)土，極限上拔承載力Qu可按下式計算：

式中：α為粘性系數(shù)；su為土的不排水剪切強度。

排水剪地基土對于均質(zhì)土，極限上拔承載力Qu可按下式計算：

式中：K為水平土應力系數(shù)；δ為基礎與土接觸面處的摩擦角。

② 掏挖擴底基礎

掏挖擴底基礎的極限上拔承載力Qu，其計算方法含三項擴底以上沿基礎表面的抗力Qsu(與不擴底基礎相同)、擴底部分剪切抗力Qb和基礎自重。

不排水剪地基土計算如下：

排水剪地基土計算如下：

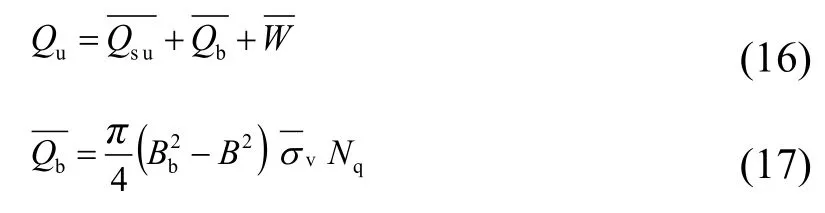
式中：Bb為擴底直徑；B為掏挖主柱直徑；v為擴底部分中點位置處的有效豎向應力；ω為由擴底引起的剪切強度衰減因子。

⑶ 摩擦圓柱體法

擴底掏挖基礎上拔承載力還有一個計算方法叫摩擦圓柱體法，它假定地基土的剪切破壞面為一圓柱體，圓柱體直徑為擴底直徑。

不排水剪地基土計算如下：

式中：Ws為破壞面內(nèi)土重。

排水剪地基土計算如下：

(2)下壓承載力計算

掏挖基礎的下壓承載力由側(cè)面和基底抗力組成，試驗表明，掏挖基礎在下壓荷載作用下其側(cè)面抗力和上拔荷載作用下側(cè)面抗力沒有明顯的區(qū)別。但是，一系列理論認為掏挖基礎下壓承載力主要來自基底抗力。

掏挖基礎的受壓承載力按下式計算：

式中：Qc為極限受壓承載力；Qtc為下壓力作用下基底抗力；Qsc為下壓力作用下側(cè)向抗力；W為基礎自重。

試驗數(shù)據(jù)表明，除了埋深較淺的掏挖基礎發(fā)生錐體破壞時側(cè)向抗力較小外，掏挖基礎的側(cè)向抗力在上拔和下壓力作用下沒有明顯的區(qū)別。故式中的Qsc計算方法同上拔基礎。

下壓荷載基底抗力Qtc按下式計算：

式中：qult為基底最大承載力；Ab為基底面積。

2.4 設計方法對比

美國標準中給出了幾種“drilled shaft”基礎的計算模型，傳統(tǒng)圓柱體剪切模型的計算結(jié)果與試驗結(jié)果最為接近。下文采用傳統(tǒng)圓柱體剪切模型進行對比。

我國掏挖基礎是以土體剪切作為基礎抗拔承載力，以基礎底面地基承載力作為下壓承載力；而美國的傳統(tǒng)圓柱體剪切模型和我國挖孔樁基礎類似，都是以端阻力、側(cè)面摩阻力和基礎自重作為抗力，不同之處主要在于擴大頭的計算模式。

3 算例

現(xiàn)取一典型的基礎設計條件用掏挖基礎、挖孔樁基礎、美國drilled shaft基礎分別進行優(yōu)化設計。設計條件如下：

基礎上拔力為1600kN，相應水平力為280kN；下壓力為1800kN, 相應水平力為300kN。

地基為粉質(zhì)粘土，硬塑，內(nèi)摩擦角15°，凝聚力30kN/m2，地基承載力250kPa。

優(yōu)化設計后的基礎主要參數(shù)見表3。

表3 基礎尺寸和材料量

由以上結(jié)果可以看出掏挖基礎材料量最大，主要原因是其計算模型為剛性樁，其下壓力和大部分的彎矩主要由底板承擔，而底板是素混凝土，底板尺寸較大才能滿足受彎和剪切的作用。而挖孔樁基礎和Drilled shaft基礎為彈性樁，考慮了樁側(cè)的摩阻力和樁側(cè)土的抗彎作用，因此底板受力較小。因此在增加基礎埋深的施工難度不大情況下，優(yōu)先采用更細長的彈性樁基礎更為經(jīng)濟。

挖孔樁基礎材料量最小，比Drilled shaft基礎材料量少得較多的原因主要在于擴大頭的作用計算方法不同，挖孔樁基礎擴大頭部分計算側(cè)向摩阻力時在不大于5倍直徑的范圍內(nèi)周長取πD，但具體取多少最為合適沒有給出說明，以上算例是按5倍直徑計算的結(jié)果；而Drilled shaft基礎擴大頭部分按土的正應力乘以其水平投影面積作為抗拔承載力。挖孔樁基礎一般埋深較淺，5倍直徑內(nèi)放大摩阻力過于冒進，建議在實際設計過程中參考Drilled shaft基礎的計算方法適當降低。

4 結(jié)論

(1)我國掏挖基礎是以土體剪切、土體重量和基礎自重作為基礎抗拔承載力，以基礎底面地基承載力作為下壓承載力；而美國的傳統(tǒng)圓柱體剪切模型和我國挖孔樁基礎類似，都是以端阻力、側(cè)面摩阻力和基礎自重作為抗力，不同之處主要在于擴大頭的計算模式。我國挖空樁基礎在樁長徑比較小的情況下高估了擴大頭的作用，需要根據(jù)具體情況適當降低。

(2)掏挖基礎計算模型下壓力和大部分的彎矩主要由底板承擔，忽略了下壓時樁側(cè)摩擦力的有利作用，造成材料量較大。因此在增加基礎埋深的施工難度不大情況下，優(yōu)先采用更細長的彈性樁基礎更為經(jīng)濟。

[1]DL/T5219-2005，架空送電線路基礎設計技術規(guī)定[S].

[2]IEEE Std 691-2001.IEEE Guide for Transmission Structure Foundation Design and Testing.