叛逆追蹤技術研究

韓金森，鄒 濤，張龍軍

(武警工程大學通信工程系，陜西西安 710086)

信息化在國防、內衛、經濟建設、科教等領域應用廣泛，在方便了人們的生產生活同時也伴隨著隱患。網絡的開放共享給不法之徒可乘之機;數字信息的易復制傳輸給了盜版侵權者可能;終端智能移動給了竊密者機會。對此，學者們提出了一系列的技術方案，如信息隱藏技術、數字水印技術、叛逆追蹤技術等。叛逆追蹤是用其算法來追蹤盜版內容或者盜版密鑰的來源，屬于追根溯源防止事態嚴重化的主動防御補救手段。該方向興起于20世紀末［1］，是涉及通信學、密碼學、計算機科學等自然學科和法律、經濟等社會學科的交叉專業。在現有發展物聯網環境下，網絡更加開放共享，加密信息廣泛通過不安全的信道接收或者分發廣播。研究叛逆追蹤技術廣泛應用于物聯網環境下的信息數據融合、在線數據庫以及基于網絡的數據分發等領域顯得尤為重要。

1 叛逆追蹤概念

叛逆追蹤(Traitor Tracing)，就是要實現在廣播發布加密信息過程中，至少找出一個和叛逆行為有關的叛逆者或盜版者，并提供檢舉的證據和終止其解密的能力和權力。在研究叛逆追蹤技術中，主要分兩個方向:基于數字水印和基于廣播加密。后者相對于前者具有更強的應用性和擴展性，通過學者長期的努力，從算法和機制的角度，加以有針對性的改進而滿足防抵賴、抗共謀、黑盒追蹤、低銷高效、支持多服務等更多要求。方案原理結構，如圖1所示。

圖1 叛逆者追蹤方案的基本模型

(1)系統初始化。主要包括安全參數設置、用戶注冊(數目為n)和密鑰(加密公鑰e和n個用戶私鑰d)生成。

(2)加密。就是數據發布者(DS)一方面利用會話密鑰s把明文P對稱加密成密文塊CB，另一方面利用系統公鑰e將會話密鑰s加密成使能塊EB。

(3)解密。就是授權用戶利用獲得的解密密鑰di解密使能塊EBi以獲得會話密鑰s，再利用獲得的會話密鑰s解密密文塊CBi以獲得明文塊Pi。

(4)追蹤。就是DS根據盜版數據或者解碼器對具有叛逆行為的授權用戶進行追蹤，并提交叛逆證據。

2 典型的叛逆追蹤方案

對于叛逆追蹤技術的研究起于20世紀90年代，已有近20年歷程，但目前還仍處于比較初級的階段:一般的系統和網絡采用傳統的信息安全手段，顯然不適合日益變化的網絡攻擊行為;通過理論研究雖然提出了各種新的方案，但對于實際不同的應用環境缺乏針對性。當前對于構造TTS的理論研究，主要基于RSA、ECC、CRT、T－函數等幾類數學困難性問題構造的方案，雖然能夠彌補不同程度的不足，但是幾類方案都有各自的利弊和有進一步發展改進的空間。

2.1 基于RSA的TTS

2.1.1 方案的產生和描述

基于大整數分解困難性假設的RSA算法是目前最為成熟的公鑰加密算法，利用其構造的TTS的基本模型如圖1所示，具有一定的典型性。2004年，MA利用RSA算法構造了一種叛逆追蹤方案［2］，可以追蹤到所有的叛逆者。但該方案中設計的會話密鑰固定不變，一旦泄露，盜版者就可以構造無法被追蹤的盜版解碼器。2006年，MA通過引入一個隨機數來克服上述問題［3］，描述如下:

(1)系統初始化。注冊用戶n，選擇大整數M=pq和向量E={e1，e2，…，en}，隨機生成n維布爾向量v(i)，計算解密密鑰參數di，分發解密密鑰DKi。

(2)加密。密文C={Pe1modM，Pe2modM，…，PenmodM}。

2.1.2 方案分析

基于RSA的TTS安全性，依賴于大整數分解的困難性假設，密文被直接成功破解的概率可以被忽略，而且對叛逆者的追蹤具有普遍性，更新撤銷用戶對其他合法用戶不影響，另外，可以根據效率和安全性需求選擇是否采用會話密鑰，具有一定的靈活性;但實際工程應用中，產生大整數和大素數的條件受到限制，而且隨著科技發展，計算速度大幅提高，密鑰長度要得到加強，整個TTS過程中各部分的算法代價有待于提高，如表1所示。

表1 傳統基于RSA的TTS過程代價

2.2 基于ECC雙線性映射的TTS

2.2.1 方案的產生和描述

ECC(橢圓曲線密碼體制)的安全性依賴于EC上加法循環群中(Bilinear Decision Diffie－Hellman，BDDH)問題求解困難性，且可證明安全。2002年Mitsynari首次構造了基于ECC的TTS［4］。其雙線性映射可由SEC(超奇異橢圓曲線)上的Weil配對或Tate配對來構造［5］，再引入 OPE［6］(不經意多項式估值協議)以構造非對稱性的TTS。方案［7］描述如下:

(1)系統初始化。在加法循環群G1的元中隨機選擇P、Q，在Zq上選取秘密多項式g(x)和秘密數b∈，得到公開密鑰K，確定解密密鑰K。pi

(2)加密。選擇會話密鑰s，M→Es(M)，DS廣播密文(H，Es(M))。

(3)解密。用戶i計算s，明文M=Ds(Es(M))。

(4)追蹤。在乘法循環群G2的元中隨機選擇R，輸入解密密鑰為Ki的盜版解碼器，輸出測試消息Ci，確定匹配的用戶i為叛逆者。

2.2.2 方案分析

基于ECC雙線性映射的TTS方案，具備ECC安全性可證明，結構簡單、構造巧妙、所耗代價小等特點;在相同安全等級情況下，密鑰長度和運算速度都較RSA有明顯的優勢。此類構造的方案密鑰被破解以及黑盒追蹤在語義上都是可證明安全的，但基于ECC的方案需要通過引入OPE等方法來實現無第三方參與的非對稱性和防誣陷性，改進黑盒追蹤能力和可撤銷性，使得其應用性更強。

2.3 基于CRT的TTS

2.3.1 方案的產生和描述

CRT(中國剩余定理)是中國數學史上的偉大發現，相對于傳統的大整數分解和循環群上離散對數問題的復雜大模指數運算受到資源的限制，SUN利用CRT構造了只使用幾個大模數的模乘法運算，只有二次復雜度的公鑰密碼算法［8］。利用CRT公鑰算法構造的TTS的安全性基于兩個數學難題，算法過程僅使用大模數乘法，效率較高［9］。方案描述如下:

(2)加密。選擇對稱加密函數E、解密函數D和哈希函數H，周期更新會話密鑰s，計算密文塊信息E(ks)=E(H(s))，使能塊信息報頭C=(z1，z2)。

(3)解密。由使能信息報頭解密會話密鑰ks;用會話密鑰解密密文塊。

(4)追蹤(黑盒追蹤)。計算并輸入盜版解碼器測試密文C'=(z'1，z'2)，判斷輸出結果非x，判定j為叛逆者。

2.3.2 方案分析

基于CRT的方案安全性依賴于兩大數學難題，被攻擊安全性同樣可被證明，而且該算法只使用了大模數的模乘法運算和低階矩陣和向量的乘法運算，在計算速度和開銷上更具優勢，也保持了良好的黑盒追蹤和可撤銷特性。

2.4 基于單圈T－函數的TTS

2.4.1 方案的產生和描述

單圈 T － 函數，2002 年，Klimov 和 Shamir［10］提出后以其高效性被廣大學者關注，先后應用于分組密碼［11］、流密碼［12］和 Hash 函數［13］。經過數年的努力，ZHANG利用其獨特的性能，構造了具有黑盒追蹤能力的 TTS［14］，描述如下:

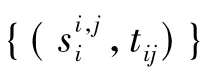
2.4.2 方案分析

基于單圈T－函數的TTS算法簡單，追蹤的復雜度o(m)=o(logu)，黑盒追蹤效率與密鑰數無關而只與桶的數量有線性關系，其安全性基于單圈函數的個數而不能以不可忽略的概率直接破解，P=lm/22n－1－n。另外，該TTS實現的硬件構成簡單，有利于量產和規模化。

3 技術難點和發展方向

叛逆追蹤研究，是信息安全方向上研究價值高、生存周期長的課題，雖然已經歷近20年，但日益發展的信息安全技術要求叛逆追蹤的研究也要與時俱進，由理論性研究向應用性研究過渡，這就需要基于各種算法的TTS能夠更好地發揮各自的優點，趨利避短地應用到特定的環境和系統中。基于RSA的TTS，存在密鑰長度的耐用性差、計算復雜度高的不足，但是該方案的安全性強，適合用于配置高、計算能力強的環境;基于ECC的TTS，計算效率比RSA的高，受到了很多學者關注，經過文獻［15］等的改進，具有了多服務、防誣陷的功能;基于CRT的TTS，速度和開銷上都具有明顯的優勢，甚至達到對稱加密的速度對于應用環境的運算速度要求不高;基于單圈T－函數的TTS，算法只有模2加，硬件只用移位寄存器，生產成本低。近年來對于叛逆追蹤的研究，幾乎都要求實現黑盒追蹤，安全而可行，下一步研究的方向，要面臨向實際應用的過渡，側重于多服務、抗重放、防抵賴易構建、能量產的研究。

4 結束語

介紹了叛逆追蹤技術的概念和原理，分析了基于不同數學難解問題的幾種方案。學者們能利用密碼算法的安全性構造叛逆追蹤方案，在確保完成準確追蹤的基礎上，重點考慮運算速度和追蹤效率，實現黑盒追蹤、可撤銷、抗重放、防抵賴等良好性質，逐步從理論向實際應用過渡。在進入物聯網時代的機遇，叛逆追蹤技術的應用將帶來更安全的信息服務。

［1］BENNY C，AMOS F，MONI N，et al.Tracing traitors［J］.IEEE Trans on Inform Theory，2000，46:893 －910.

［2］馬華，曹正文.基于RSA加密算法的叛逆追蹤方案［J］.西安電子科技大學學報:自然科學版，2004，31(4):611－613.

［3］馬華，楊波.改進的基于修改RSA的叛逆者追蹤方案［J］.西安電子科技大學學報:自然科學版，2006，33(3):422－424.

［4］MITSUNARI S，SAKAI R，KASAHARA M.A new traitor tracing［J］.IEICE Transactions on Fundamentals of Electronics，Communications and Computer Sciences，2002，E85－A(2):481－484.

［5］BONEH D，FRANKLIN M.Identity based encryption from the weil pairing［C］.Proc.of The 21st Annual International Cryptology Conference on Advances in Cryptology.London.UK:Springer－Verlag，2001:213 －229.

［6］NAOR M，PINKAS B.Oblivious Transfer and Polynomial E-valuation［C］.NY，USA:Proc.of the 31st Annual ACM Symposium on Theory of Computing，1999:245 －254.

［7］呂錫香，張衛東，楊文峰.基于雙線性映射的非對稱公鑰叛逆者追蹤［J］.計算機工程，2009，35(3):4 －6.

［8］孫秀娟，金民鎖，姜文彪.基于CRT的公密碼算法應用研究［J］.重慶科技學院學報:自然科學版，2010，12(6):162－164.

［9］張學軍，王東勇，曾智勇，等.一種新的具有附加特性的叛逆者追蹤方案［J］.西安電子科技大學學報，2007，34(2):274－278.

［10］KLIMOV A，SHAMIR A.A new class of Invertible mappings［J］.LNCS，2002(2523):470 －483.

［11］KLIMOV A.Applications of t－ functions in cryptography［D］.The State of Israel: Weizmann Institute of Science，2005.

［12］ALEXANDER K，ADI S.New cryptographic primitives based on multiword t－ functions［J］.LNCS，2004(3017):1 －15.

［13］KLIMOV A，SHAMIR A.Cryptographic applications of tfunctions［J］.LNCS，2003(3006):248 － 261.

［14］張玉麗，蔡慶軍.一個高效的基于單圈T－函數的叛徒追蹤方案［J］.計算機工程，2009，45(11):97 －98.

［15］張學軍，周利華，王育民.改進的基于雙線性映射叛逆者追蹤方案［J］.北京郵電大學學報，2006，29(6):17－20.