基于FPGA的IIR帶通數(shù)字濾波器設(shè)計與仿真
杭州電子科技大學(xué)射頻電路與系統(tǒng)教育部重點實驗室 楊延亮 程知群 馮 濤
基于FPGA的IIR帶通數(shù)字濾波器設(shè)計與仿真
杭州電子科技大學(xué)射頻電路與系統(tǒng)教育部重點實驗室 楊延亮 程知群 馮 濤
該文給出了用Matlab設(shè)計IIR帶通數(shù)字濾波器的方法,利用Matlab語言進行程序設(shè)計出二階環(huán)為基礎(chǔ)的并聯(lián)結(jié)構(gòu)模型,通過在Matlab環(huán)境下仿真軟件Simulink對設(shè)計的帶通濾波器進行了動態(tài)仿真,確定了濾波器系數(shù)的量化字長。從仿真結(jié)果來看,設(shè)計的帶通數(shù)字濾波器既滿足濾波器的選頻特性,又優(yōu)化了硬件資源。在實際的應(yīng)用中,可以根據(jù)不同F(xiàn)PGA資源靈活修改濾波器系數(shù),在不同規(guī)模的FPGA上實現(xiàn)。
無限脈沖響應(yīng);帶通數(shù)字濾波器;量化字長;現(xiàn)場可編程門陣列
1.引言
在數(shù)字信號處理的領(lǐng)域內(nèi),數(shù)字濾波技術(shù)是極其重要的一個分支。無論是信號的獲取、傳輸,還是信號的處理和交換都離不開數(shù)字濾波,它對于信號安全有效的傳輸是至關(guān)重要的[1]。在主要的兩類數(shù)字濾波器中,IIR(無限脈沖響應(yīng))濾波器被廣泛使用。
Matlab是美國MathWorks公司出品的數(shù)學(xué)軟件,用于算法開發(fā)、數(shù)據(jù)可視化、數(shù)據(jù)分析以及數(shù)值計算的高級技術(shù)計算語言和交互式環(huán)境[2]。其中Matlab自帶的信號處理工具箱,具有強大的信號處理和分析功能,它提供了豐富簡便的設(shè)計,使原來繁瑣的程序設(shè)計簡化成函數(shù)的調(diào)用,這樣便可以快速有效的實現(xiàn)數(shù)字濾波器的設(shè)計與仿真。
FPGA(現(xiàn)場可編程門陣列)以其優(yōu)越的實時性和設(shè)計靈活性成為了控制系統(tǒng)中不可或缺的一部分,它可利用Simulink設(shè)計仿真的有限字長IIR濾波器自動生成VHDL或Verilog代碼,下載至FPGA實現(xiàn)濾波器功能[3]。本文研究了基于FPGA有限字長的IIR帶通數(shù)字濾波器的相關(guān)理論,設(shè)計方法及仿真。
2.IIR數(shù)字濾波器設(shè)計基本原理
數(shù)字IIR濾波器的設(shè)計都是基于模擬IIR濾波器,之后將其轉(zhuǎn)化為等價的數(shù)字濾波器[4]。其中沖擊響應(yīng)不變法是一種較為常用的方法。其總的變化流程如下:
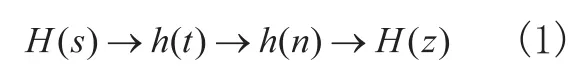
考慮到傳統(tǒng)濾波器計算量大,濾波特性不宜調(diào)整等缺點,如何解決這些問題便顯得極為關(guān)鍵。利用Matlab強大的數(shù)字信號處理和計算能力可快速有效的設(shè)計數(shù)字濾波器,不僅極大的簡化了計算量,而且它可以隨時對比設(shè)計要求和濾波器特性進行參數(shù)調(diào)整,方便靈活[5]。
3.基于FPGA的IIR濾波器設(shè)計
3.1 濾波器設(shè)計方法的選擇
高階IIR數(shù)字濾波器的系統(tǒng)傳遞函數(shù)可表示為:
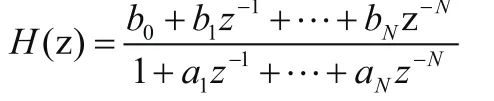
根據(jù)濾波器傳遞函數(shù)H(z)的不同表達(dá)形式,可以得出不同的實現(xiàn)結(jié)構(gòu)。相對較為常用的3種結(jié)構(gòu)為直接型,級聯(lián)型和并聯(lián)型。其中直接型對系數(shù)的敏感度最高,受有限字長造成的影響最大。級聯(lián)型H(z)的連接順序具有很大的自由度,因此在實際設(shè)計中這些組合方式,比例變化和H(z)的連接順序等都會產(chǎn)生很大的問題。并聯(lián)型濾波器則可以很好的克服上述兩種結(jié)構(gòu)的缺點,因此在濾波器極點不重復(fù)時,并聯(lián)型濾波器被廣泛使用。
在相同性能的要求下,橢圓濾波器比巴特沃斯和切比雪夫濾波器所需的階數(shù)低,且過渡帶窄,可獲得更好的選頻特性。
3.2 Matlab程序設(shè)計
通過Matlab設(shè)計的帶通濾波器部分代碼如下:

上述程序給出了橢圓濾波器模型設(shè)計的10階并聯(lián)型結(jié)構(gòu)的數(shù)字濾波器[6]。通帶為頻率1000~2000Hz,采樣頻率8000Hz,通帶衰減1dB,阻帶衰減60dB。
3.3 濾波器穩(wěn)定性問題
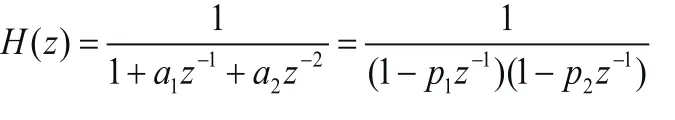
二階IIR濾波器傳遞函數(shù)為:從式中可以看出,為確保穩(wěn)定性,極點必須位于單位圓之內(nèi)(即|p1|<1,|p2|<1),因此可以得到:
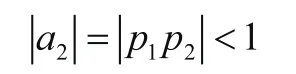
由Schur-Cohn穩(wěn)定性測試可以得到a1和a2的關(guān)系為:

只要滿足上述兩式的關(guān)系,就可以保證濾波器的穩(wěn)定性。
理論設(shè)計出的濾波器系數(shù)是無限精度的,但在實際的應(yīng)用中,所有的系數(shù)都必須是以二進制數(shù)儲存在計算機中,這就要求量化系數(shù),取有限精度的字長,相應(yīng)造成濾波器零極點的位置發(fā)生偏移,使得實際的頻率響應(yīng)和理論情況有所出入,情況嚴(yán)重時還可能使濾波器極點偏移至穩(wěn)定單位圓外,造成整個系統(tǒng)不穩(wěn)定。
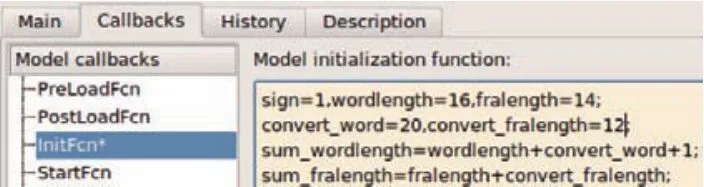
圖1 初始化函數(shù)
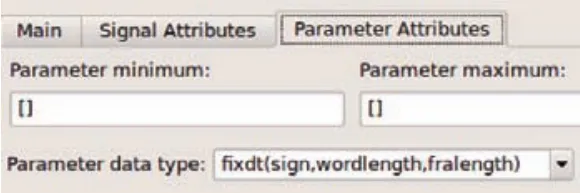
圖2 濾波器系數(shù)參數(shù)
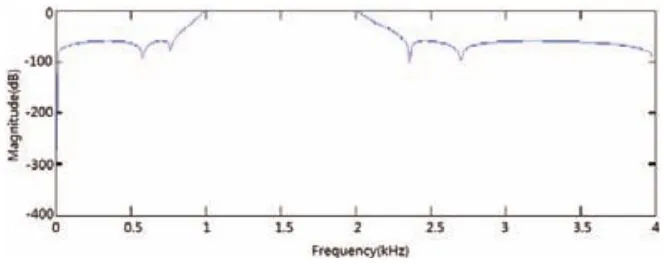
圖3 未經(jīng)量化的幅頻響應(yīng)
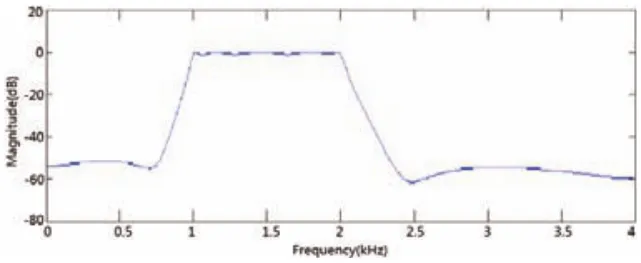
圖4 量化精度16bits幅頻響應(yīng)
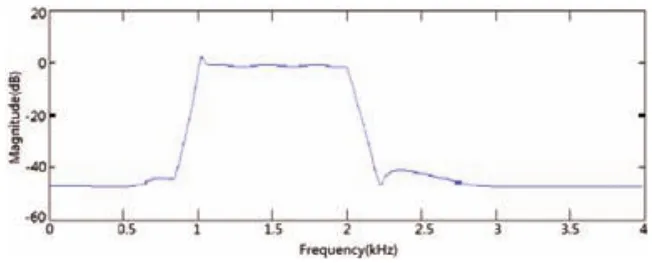
圖5 量化精度14bits幅頻響應(yīng)
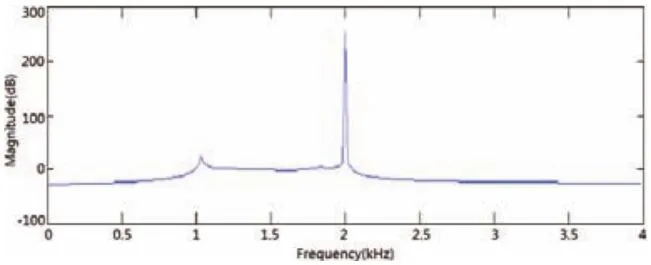
圖6 量化精度13bits幅頻響應(yīng)
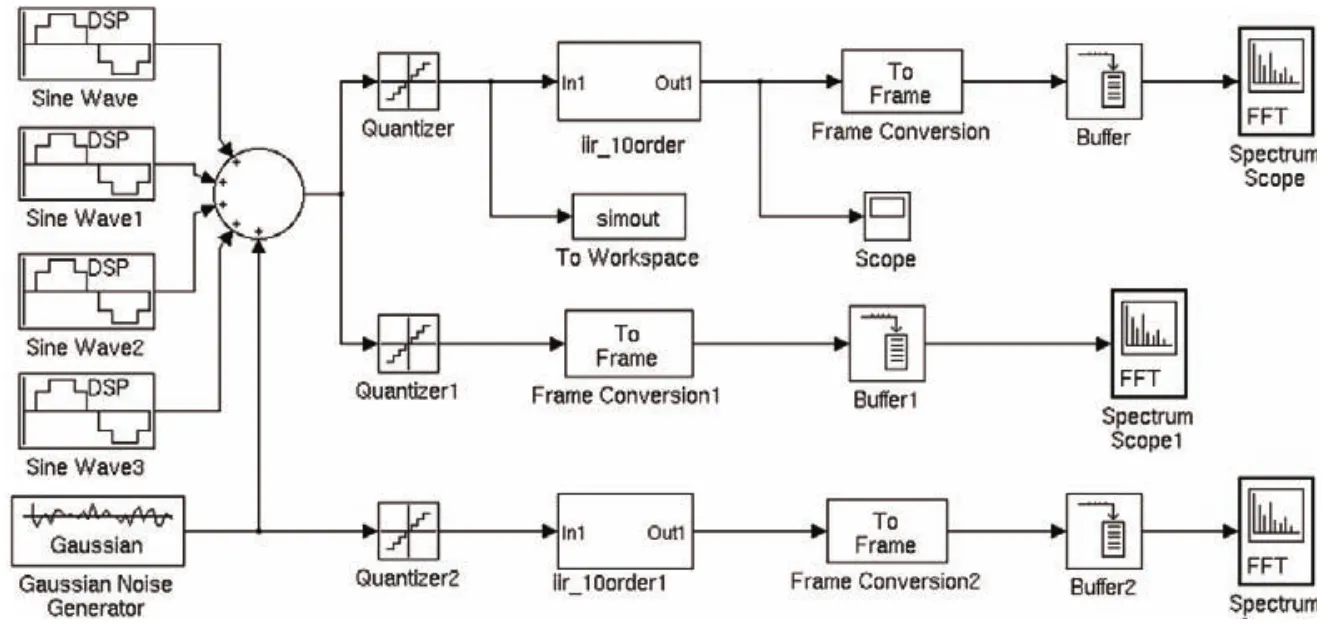
圖7 IIR濾波器Simulink仿真模型
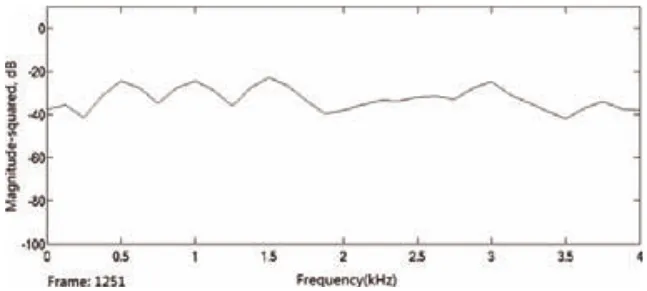
圖8 4單頻與白噪聲相加頻譜
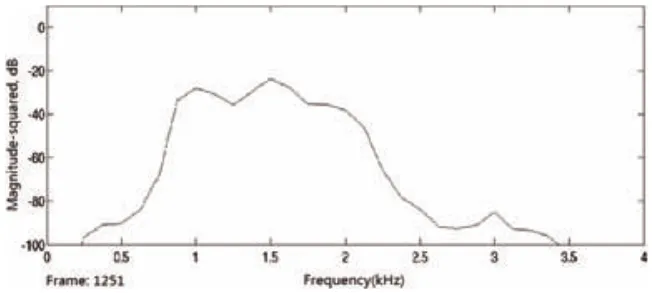
圖9 單頻加白噪聲濾波后頻譜
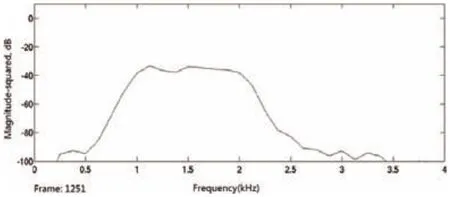
圖10 白噪聲濾波后的頻譜
導(dǎo)致這些不穩(wěn)定的因素主要有兩方面體現(xiàn):溢出和極限環(huán)。溢出問題可以通過飽和模式、保護位、對信號和/或系數(shù)進行縮放等消除溢出效應(yīng);而對于極限環(huán)所造成的不穩(wěn)定,可以通過截尾法、降低濾波器階數(shù)、使用更多位來提高精度,移動極點使其遠(yuǎn)離單位圓等方法來消除極限環(huán)[7]。總之,在FPGA上實現(xiàn)IIR濾波器之前,檢查其穩(wěn)定性和有限字長效應(yīng)是非常重要的。
3.4 濾波器系數(shù)量化精度造成的影響
在Simulink濾波器模型中,可以通過設(shè)定變量的方法可靈活控制濾波器系數(shù)字長,如圖1、2所示。
在圖2所示的Parameter Attributes和Signal Attributes分別對應(yīng)的data type中可對其進行變量設(shè)定;圖1所示的InitFcn函數(shù)可以對濾波器系數(shù)、加法器等設(shè)定與圖2相對應(yīng)的變量,并對其初始化。其優(yōu)勢在于當(dāng)需要改變?yōu)V波器字長時,無需通過對每個濾波器系數(shù)字長逐一進行修改,只需在InitFcn函數(shù)中對其對應(yīng)的初始化常量值進行修改量化即可。不同的量化字長對應(yīng)不同的濾波效果,對幅頻響應(yīng)造成的影響如圖3-6所示。A子集還是B子集進行編碼。反過來也可以說,左側(cè)數(shù)據(jù)區(qū)字符編碼的奇偶排列順序,決定了前置碼。比如,如果某個條形碼的左側(cè)數(shù)據(jù)區(qū)的編碼是:奇偶偶偶奇奇,那么前置碼就是6。
3.5 條碼譯碼
經(jīng)由條碼的條空寬度歸一化到-1,-2,-3,-4,1,2,3和4八個整數(shù)后,創(chuàng)建譯碼表,表3所示。譯碼工作通過查詢此表即可實現(xiàn)。例如:某個字符的四個條空寬度分別是,-3,1,-2和1,經(jīng)查表可知,這個字符是“8”。
4.實驗結(jié)果分析
仿真實驗使用VC++ Express 2008和OpenCV開發(fā)平臺。實驗表明,本文算法效果良好。對于光照不均勻,輕微模糊,及傾斜角在正負(fù)25度內(nèi)的條碼圖像,都能正確識別。如圖7所示。
[1]中國標(biāo)準(zhǔn)出版社.條碼國家標(biāo)準(zhǔn)匯編[M].北京:中國標(biāo)準(zhǔn)出版社,2004.
[2]陸宗騏.C/C++圖像處理編程[M].北京:清華大學(xué)出版社,2005.
[3]蘇彥華.VC++數(shù)字圖像識別技術(shù)典型案例[M].北京:人民郵電出版社,2004
[4]沈庭芝.數(shù)字圖像處理及模式識別[M].北京:北京理工大學(xué)出版社,1998.
姜亮(1980—),男,研究生,研究方向:計算機應(yīng)用。

