單電磁鐵懸浮系統的指數趨近律滑模控制

宋榮榮

(1.西南交通大學電氣工程學院，成都 610031;2.西南民族大學計算機科學與技術學院，成都 610041)

磁浮控制技術能夠使懸浮物與支承面實現無接觸懸浮，具有無摩擦、噪聲低、污染小等優點，因而被廣泛應用在磁懸浮軸承、磁懸浮工作臺、磁懸浮隔振器，特別是磁懸浮列車上，這使得該技術受到國內外專家和學者的廣泛關注［1］。一般來說，磁浮控制方法主要包括線性控制［2］和非線性控制［3］。目前，很多國內外專家學者對磁浮系統的滑模控制產生了濃厚的興趣［4］。

線性控制主要是通過將系統在平衡點的鄰域內采用泰勒定理展開，用近似的線性結構代替非線性結構進行懸浮控制。Matsuda R［5］研究了多電磁鐵懸浮系統的線性化問題，并設計了一種反饋控制器。由于軌道具有不平順的隨機性，Hac A［6］設計了一種預見控制器，該控制器對線性懸浮系統的運行平穩性、外干擾和工作狀態具有良好的預見性。Trumper D L［7］提出了一種系統線性化的方法，利用線性和非線性2種控制器對系統進行仿真比較。為了實現故障檢測，在傳統Luenberger觀測器的基礎上，Koseki T［8］對系統的線性化模型提出了一種Luenberger魯棒故障檢測觀測器的設計方法以及相應的故障檢測算法，并給出了在外干擾存在的情況下，實現魯棒故障檢測觀測器設計的充分必要條件。然而，這些控制方法只能使系統在平衡點附近具有良好的性質，在遠離平衡點處，系統將處于不穩定狀態。

磁浮系統是一種典型的非線性、不確定性開環系統。傳統的控制方法無法解決非線性部分的控制問題，所以目前國際上有很多專家學者都在研究懸浮系統的非線性控制方法，例如H∞魯棒控制、數控技術、狀態最優估計控制、神經網絡控制、模糊控制等，這些控制方法對于解決磁浮系統的非線性和不確定性有著良好的效果［9－13］。

在眾多的控制方法中，滑模控制對內部參數的變動和外部擾動具有完全的自適應性，這一優點已引起專家學者的極大興趣，使其得到巨大發展和廣泛應用。多年以來，許多學者將這項技術應用到懸浮控制技術中。針對3種模式下的靜電懸浮系統，Yang W Q等［14］設計了滑模控制器，仿真研究表明，該控制器提供了一個保證系統良好性能的預載荷。對于懸浮系統，Mohan B［15］結合最優控制和自適應控制算法設計了一個滑模控制器，該控制器能夠保證系統在外干擾和系統參數發生改變時保持良好的性能，但是不能有效消除抖振現象。抖振問題的確是滑模控制的一個缺點，這成為影響滑模控制發展的主要原因。對于一個帶有積分結構的線性系統，楊普等［16］采用指數趨近律設計了滑模控制器，給出了抖振幅度、周期和趨近律參數、控制量的變化率之間的定量關系，從而有效地控制系統的抖振問題。基于以上文獻，本文將滑模控制技術應用到單電磁鐵的懸浮控制中，并采用指數趨近律有效地解決了該系統的抖振問題。

本文先給出磁場力的一種非線性結構，通過控制電流，將該系統轉化為二階非線性系統。然后，根據系統的狀態方程，設計了一個具有防抖振現象的動態滑模控制器。最后，基于Matlab軟件進行了仿真。結果表明，該控制系統具有良好的動態性能和較強的魯棒性。

1 單電磁鐵懸浮系統的狀態方程

在單電磁鐵懸浮系統中，磁鐵懸浮在電壓控制的磁場中，所以系統可以通過控制器控制電流，從而控制電壓，使磁鐵懸浮在設定的平衡點處。系統結構如圖1所示。

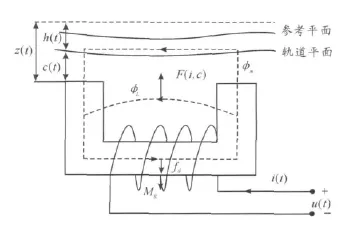
圖1 單電磁鐵懸浮系統結構

圖1中:φT為主極磁通;φm為氣隙磁通;φL為漏磁通;Mg為電磁鐵重力;fd為外界干擾力;F(i，c)為電磁吸力;z(t)為磁極表面與參考平面的距離;h(t)為導軌表面參考平面的距離;c(t)為磁極與導軌間的氣隙;i(t)為控制線圈的電流;u(t)為繞組回路的電壓。

在分析單電磁鐵懸浮系統的動力學模型時，假設［17］:

① 忽略漏磁通 φL，即 φm=φT。

②電磁鐵磁路中鐵磁材料的磁導率無窮大(忽略鐵芯和導軌中的磁阻)，磁勢均勻降落在氣隙上。

③電磁鐵僅有垂直方向上的移動，其他方向受限，無運動。

設電磁鐵懸浮位置為c，控制電流為i，兩者之間的關系如表1。

表1 c與i的關系

電磁鐵受到的磁場力F與c和i有關，可用下式表示:

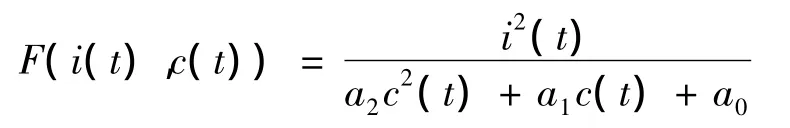
式中a2、a1、a0為待定系數。利用最小二乘法擬合曲線，由 表 1 可 得 a2=0.019 5，a1=－0.182 7，a0=0.133 8。

根據電磁場理論，系統的數學模型為

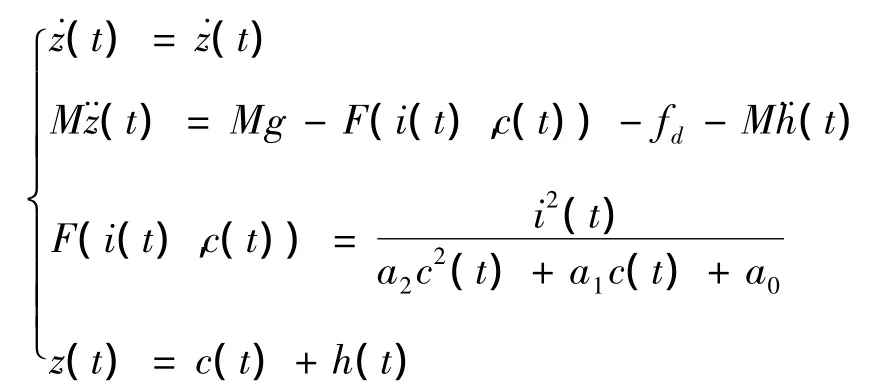
選取系統狀態變量為x1(t)=c(t)，x2(t)=，那么單電磁鐵懸浮系統的狀態空間方程為

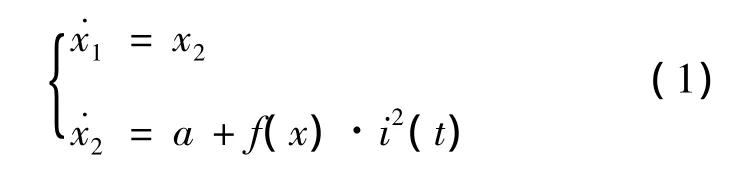
設 x0=(x10，x20)=(x10，0)為系統在平衡點處的狀態值，系統輸出y=x1－x10，由式(1)可得輸入輸出關系¨y=a+f(x)·i2(t)。這樣，就建立了單電磁鐵懸浮系統的狀態方程。

2 滑模控制器

滑模控制不是一種分析方法，而是一種綜合方法，因此，其重點就是系統的設計問題［22］。

設計問題有2個:① 選擇切換函數 s(x);②求取控制u±(x)。設計的目標有3個，即滑模控制的三要素:進入條件;存在條件;穩定條件。

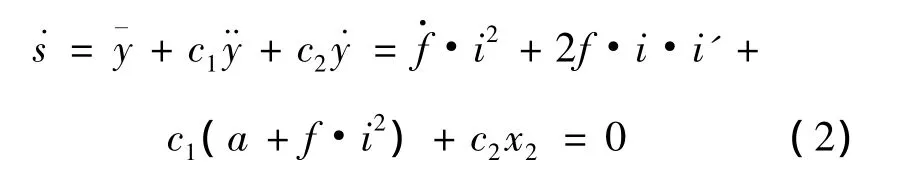
可得系統在滑模區的等效控制

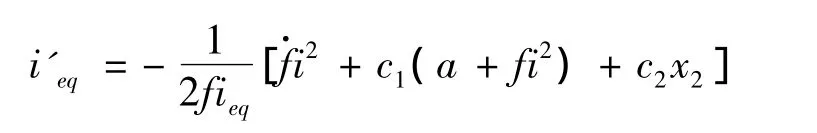
將ieq代人系統表達式(1)，可得滑模運動方程

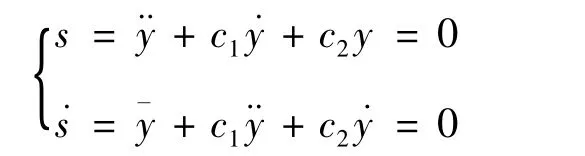
那么，等效的滑模運動方程可寫為

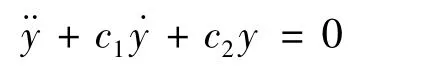
其中參數c1、c2滿足 Hurwitz多項式 p(s)=s2+c1s+c2的要求，這樣就可使得滑模運動漸近穩定。

利用式(1)，可以將切換函數改寫為s=a+fi2+c1x2+c2(x1－x10)。采用指數趨近律－w*sign(s)－Ks的控制策略，則得控制電流:

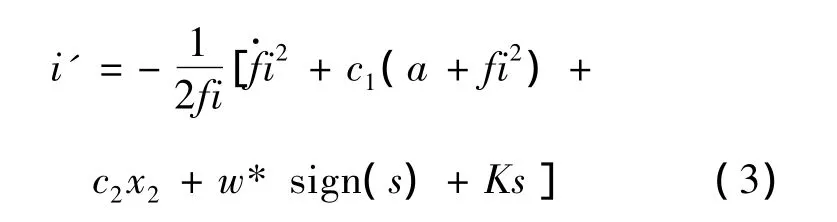
當切換函數s趨近于零時，輸出y=x1－x10可以通過方程得到。因為參數c1、c2滿足Hurwitz多項式p(s)=s2+c1s+c2的要求，所以輸出y趨近于零，這樣x2也將趨近于零。通過滑模控制，就可以保證系統中的單電磁鐵到達期望的位置。

3 Matlab仿真分析

對于單電磁鐵懸浮系統，選擇參數為:采樣周期為0.01 s，重力加速度g=9.8 m/s2，電磁鐵質量m=98.4 g，氣隙的初始位置x10=3.2 mm。滑模控制器參數為:w=5 000，c1=61，c2=930，K=10 000。對上面的模型用 Matlab進行仿真［19］，仿真結果如圖2所示。

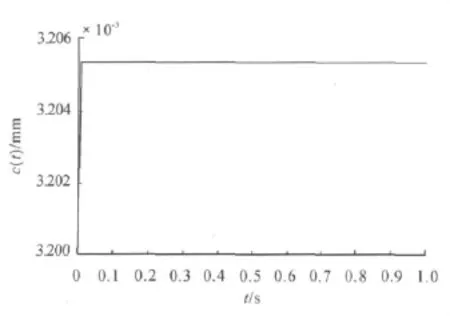
圖2 滑模控制的氣隙響應曲線

由圖2可知，對于磁懸浮系統，基于指數趨近律的滑模控制器的輸出響應過渡過程很短，能夠快速到達期望位置，滑模控制器的輸出電流約為0.93，驗證了控制器的準確性。

為檢驗采用滑模控制后系統的魯棒性，作如下仿真分析:

1)設系統參數發生改變，電磁鐵質量m=50 g，氣隙的初始位置x10=4.2 mm，氣隙變化如圖3所示。

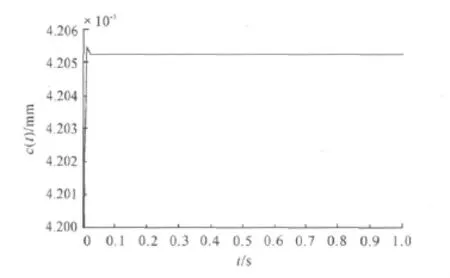
圖3 內部參數發生改變后的氣隙響應曲線

由圖3可知，系統在滑模控制器的控制作用下，不受內部參數改變的影響，仍保持良好的動態特性。

2)假設外干擾力fd增大為電磁鐵質量的3倍時，氣隙變化如圖4所示。

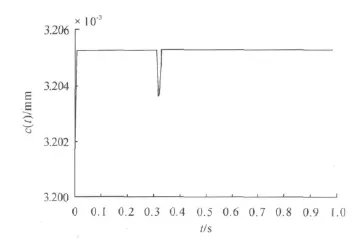
圖4 外干擾力fd增大為電磁鐵質量3倍時的氣隙響應曲線

3)當軌道振動變化大小為1 mm時，不同頻率對系統氣隙變化的影響情況如圖5所示。

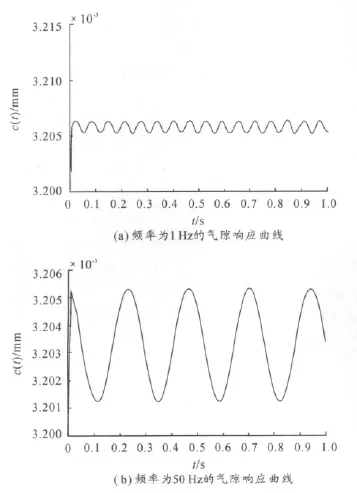
圖5 不同頻率對氣隙響應曲線的影響

仿真結果表明，當軌道變化頻率為1 Hz時，氣隙響應曲線變化幅值約為0.001 mm;當軌道變化頻率為50 Hz時，氣隙響應曲線變化幅值約為0.004 mm。

4)采用等速趨近律˙s=－w*sign(s)進行仿真比較，系統的氣隙響應曲線出現明顯的抖振現象，如圖6所示。

從仿真結果可以看出:圖6(a)表明基于等速趨近律的滑模控制器的仿真曲線中很明顯存在著一些抖振現象;而圖6(b)表明基于指數趨近律的滑模控制器的仿真曲線減弱了系統的抖振現象，說明該控制器能夠有效地解決系統的抖振問題。

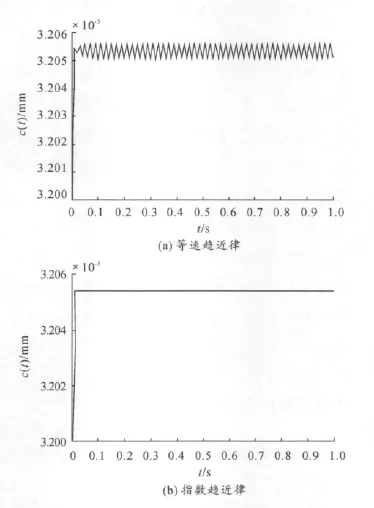
圖6 兩種不同趨近律的氣隙響應曲線

4 結論

1)分析了傳統滑模控制器必須考慮的問題:到達條件，滑模面存在條件，滑模面的設計，穩定性條件。針對單電磁鐵懸浮系統進行了改進的滑模控制器設計，即采用指數趨近律設計滑模控制器，在采樣周期為0.01 s的情況下，該系統在滑模控制器的作用下能夠較快收斂到期望的穩定位置，并保持穩定性。這說明該控制器具有較快的收斂性。

2)對于周期性的高頻和低頻干擾或是脈沖干擾，基于指數趨近律的滑模控制器都表現了很好的魯棒性，不僅響應時間短，而且氣隙響應曲線幾乎沒有出現抖振現象。總之，該系統對內部參數變化和外部干擾具有較強的魯棒性。

3)對滑模控制方法中存在的抖振現象進行了仔細分析，并采用了2種控制率對該系統進行了仿真比較。當采用等速趨近律設計滑模控制器時，該系統很明顯出現較強的抖振現象。與之相比，采用指數趨近律的控制器能夠有效地防止抖振現象。

4)一個理論必須在實踐中得到成功的應用才能推動其不斷完善和向前發展，滑模控制理論也是一樣，今后應該更多考慮如何將其和其他的非線性控制方法結合，更好地應用到磁懸浮控制中去。

［1］吳祥明.磁浮列車［M］.上海:上海科學技術出版社，2003:15－30.

［2］Trumper D L，Olson S M，Subrahmanyan P K.Linearing control of magnetic suspension systems［J］.Control Systems Technology，1997，5:427 －438.

［3］Alleyne A，Hedrick J K.Nonlinear adaptive control of active suspendsions［J］.Control Systems Technology，1995，3:94 －101.

［4］Shiuh-Jer Huang，Wei-Cheng Lin.Adaptive fuzzy controller with sliding surface for vehicle suspension control［J］.Fuzzy Systems，2003，11:550 －559.

［5］Matsuda R，Nakagawa M，Yamada I.Multi input-output control of magnetically suspended linear guide［J］.Magnetics，1984，20(5):1690 －1692.

［6］Hac A.Optimal linear preview control of active vehicle suspension［C］//Decision and Control 1990，Proceedings of the 29thIEEE Conference on.［S.l.］:［s.n.］，1990:2779－2784.

［7］Trumper D L，Olson S M.Subrahmanyan P K.Linearizing Control of Magnetic Suspension［J］.Systems，control systems technology，1997，5(4):427 －438.

［8］Jiangheng Liu，Koseki T.3 degrees of freedom control of semi-zero-power magnetic levitation suitable for two-dimensional linear motor［C］//Electrical Machines and Systems 2001 Conference.［S.l］:［s.n.］，2001:976－981.

［9］Sammier D，Dugard L.H∞control of active vehicle suspensions［C］//Control Applications，2000.Proceedings of the 2000 IEEE International Conference on.［S.l］:［s.n.］，2000:976 －981.

［10］盛蓉蓉.懸浮控制方法的研究與數字實現［D］.成都:西南交通大學，2006.

［11］Selamat H，Alimin A J，Zawawi M A.Optimal control of railway vehicle system.Industrial Technology［C］//ICIT2009，IEEE International Conference on.［S.l］:［s.n.］，2009:1 －6.

［12］Jing Xu，Juntao Fei.Neural network predictive control of vehicle suspension［C］//Information Science and Engineering(ICISE)，2010 2ndInternational Conference on.［S.l］:［s.n.］，2010:1319 －1322.

［13］Chuanyin Tang，Guangyao Zhao，Wei Zhou，et al.Research on suspension system based on fuzzy logic control［C］//Advanced Computer Control(ICACC)，2010 2ndInternational Conference on.［S.l］:［s.n.］，2010:5－8.

［14］Yang W Q，Zhang Y S.Electrostatic suspension system with sliding mode control［J］.Aerospace and Electronic Systems，1992，28:605 －609.

［15］Mohan B，Phadke S B.Variable structure active suspension system［C］//Industrial Electronics，Control，and Instrumentation，Proceedings of the 1996 IEEE IECON 22nd International Conference on.［S.l］:［s.n.］，1996:1945－1948.

［16］楊普，張曾科.一類滑模變結構控制系統的抖振控制［J］.清華大學學報，2005，45(1):93 －95.

［17］謝云德，常文森.電磁型(EMS)磁懸浮列車系統鉛垂方向的建模與仿真［J］.鐵道學報，1996(4):47－54.

［18］王豐堯.滑模變結構控制［M］.北京:機械工業出版社，2001:5－20.

［19］張智星.Matlab程序設計與應用［M］.北京:清華大學出版社，2002:360－365.