廣義向量擬似變分不等式的通有穩定性和本質連通區

李盛強

(重慶大學數學與統計學院，重慶 401331)

本質區在穩定性的研究中是一個重要的工具。1950年，Fort［1］首先提出從緊度量空間映射到自身的一個連續映射的本質不動點的概念，并且證明了任意的映射都可以大致接近于一個不動點都是本質的映射。由于即使是恒同映射也不一定存在本質不動點，1952年Kinoshita［2］提出了不動點集本質區的概念，并且證明了從Hilbert空間映射到自身的任意連續映射都至少存在一個不動點集的本質區。受到以上研究成果的啟發，Wu和Jiang［3］引入了有限博弈的本質Nash均衡點的概念，并證明了任意的有限博弈大致接近于Nash均衡點是本質的博弈。之后，Jiang［4］引入了Nash均衡點集本質區的概念，并且證明了每個有限博弈都存在至少1個Nash均衡點集的本質區。1986年Kohlberg和Mertens［5］提出對于有限博弈，一個較為滿意的解的概念應該稱為Nash均衡點集的本質區，并且證明對于任何有限博弈都存在Nash均衡點集的有限區，其中至少1個區是本質的。1990年Hillas［6］提出了從另一種方法研究穩定性，這與傳統的從Nash均衡點的擾動問題研究穩定性不同。近些年來，Yu、Yang、Luo、Xiang、Isac、Lin等將本質區的概念引入各種非線性問題中，如Ky Fan問題、均衡問題、變分不等式問題以及向量優化問題等。

近些年來，變分不等式的理論是研究非線性分析的一個重要方向。1980年以來，關于廣義向量擬似變分不等式解的存在性已經有相當多的研究成果，但是廣義擬似變分不等式的解不一定唯一，所以該問題的穩定性研究就顯得很重要。傳統研究穩定性的方法是對問題進行參數擾動后求解集對參數的各種連續性結果，即研究解集映射S(p)的連續性。1999年，俞建［7］利用Fort、吳文俊與江嘉禾所提出了本質解的概念與Mertens提出的本質連通分支的概念，研究了擬變分不等式的解集的穩定性，證明了這類擬變分不等式的解集具有通有穩定性且本質連通區是存在的。羅群、鄧曉紅［8］研究了廣義向量似變分不等式解集的通有穩定性。2007年，陳建塵、龔循華［9］提出了廣義擬變分不等式解集的穩定性及本質連通區的存在性。本文綜合了近些年來在變分不等式通有穩定性及本質連通區方面的研究方法，研究了更為廣泛的廣義向量擬似變分不等式問題的通有穩定性及本質連通區，并且更進一步地研究了本質連通區的穩定性。

1 預備知識及定義

廣義向量擬似變分不等式(GVQVLI):設E是Banach空間，X、Y是2個Hausdorff拓撲線性空間，K是X的非空閉凸子集，T:K→2L(E，Y)，S:K→2K，η:K×K→E，尋找，使得對任意的，存在，滿足

定義1 稱Q?X是X中的一個剩余集，若Q包含一列X中稠密開集的交。

引理1 考慮GVQVLI(S，T，η)問題，假設滿足條件:① S是K上連續緊凸值映射，且對任意x∈K有intS(x)≠?;②T在K上是上半連續緊凸值映射;③ η(·，·)在K×K上是連續的;④ 固定x∈K，η(·，x)是仿射的;⑤ 對于任意x∈K，如果x∈intG(x)，則η(x，x)=0。則廣義向量擬似變分不等式有解。

引理2 設X是度量空間，A，An∈K(X)滿足對任意的O?A，存在自然數N，使得對任意的n＞N，都有An?O，則任一滿足xn∈An的序列 { xn}必有聚點x*∈A。

備注1 設(X，d)為度量空間，記K(X)表示X的所有非空緊子集全體，CK(X)表示X的所有非空緊凸集全體。空間 K(X)和 CK(X)的拓撲由 Hausdorff度量 h產生，h定義如下:h(C，D)=，其中

引理3 設(X，d)為度量空間，h表示由d誘導的Hausdorff度量，則(CK(X)，h)在(K(X)，h)中閉。

2 廣義向量擬似變分不等式的通有穩定性

令 E、X、Y、S、T 和 η 的定義不變，設

對任意的 u1=(S1，T1，η1)，u2=(S2，T2，η2)∈M，定義

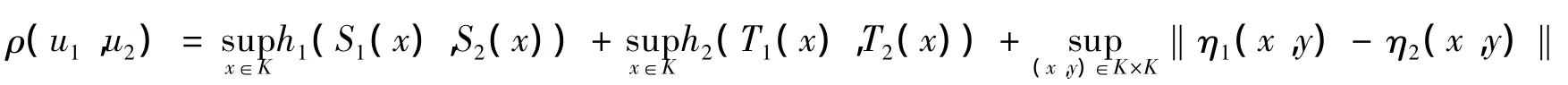
其中 h1、h2是 CK(K)和 CK(L(E，Y))上的 Hausdorff度量。

定理1(M，ρ)是完備度量空間。

證明(M，ρ)是度量空間，顯然成立，只需證(M，ρ)是完備的。

設 {un=(Sn，Tn，ηn)}是 M 中的 Cauchy列，則?ε ＞0，?N，使得對于?n，m ＞N 有 ρ(un，um)＜ ε，從而?x，y∈K，都有 h1(Sn(x)，Sm(x))＜ ε，h2(Tn(x)，Tm(x))＜ ε，‖ηn(x，y)－ ηm(x，y)‖ ＜ ε。由于{ Sn(x)}是CK(K)中的Cauchy列，{ Tn(x)}是CK(L(E，Y))中Cauchy列，(E，‖·‖)是Banach空間，由引理3 知，存在 S(x)∈CK(K)，T(x)∈CK(L(E，Y))，η(x，y)∈X，使得

下面證 T 是上半連續的，S 是連續的，η(·，·)是連續且 η(·，x)是仿射的，η(x，x)=0。

1)?x0∈K。要證T(x0)是下半連續的，只需證對于?x0的鄰域U，?x∈U，?T(x0)鄰域O，使得T(x)?O。由于 ?ε0＞ 0，所以 {ξ:d(ξ，T(x0))＜ε0}?O。下證 T(x)? {ξ:d(ξ，T(x0))＜ε0}。令，其 中又且由于Tn→T，故 h2(Tn(x)，T(x))≤ε0/3，h2(Tn(x0)，T(x0))≤ε0/3，而由 Tn的下半連續性有，所以

故 T(x)? {ξ:d(ξ，T(x0))＜ε0}?O，即T(x)在K上是上半連續的。

2)要證 S在 K上是連續的，只需證?x0∈K，?ε＞0，?x0的鄰域 N(x0)使得?x∈N(x0)有h1(S(x)，S(x0))＜ε。由于對于?x∈K，有 h1(S(x)，S(x0))≤h1(S(x)，Sn(x))+h1(Sn(x)，Sn(x0))+h1(Sn(x0)，S(x0))，且由知，存在N當n＞N時，有，又由 Sn的連續性知，?的鄰域 N()，有，所以由以上知，h(S(x)，1，于是S在K上是連續的。

3)η(·，·)的連續性證明方法與2)相同，只需將測度h2換成‖·‖即可。因ηn(·，x)是仿射的，故ηn(·，αx+b)= αηn(·，x)+ηn(·，b)，兩邊同時取極限得 η(·，αx+b)=αη(·，x)+η(·，b)，故 η(·，x)也是仿射的。又 ηn(x，x)=0，?x∈intS(x)，則對于?x∈intS(x)，存在 { xn}，滿足 xn∈intSn(xn)，那么就有ηn(xn，xn)=0。由于，且 ηn連續，故兩邊取極限得 η(x，x)=0。

由以上1)、2)、3)知，(M，ρ)是完備度量空間。

由于對于任意的u=(S，T，η)∈M，引理1表明GVQVLI有解。記Φ(u)是GVQVLI問題關于u的一個解集，則Φ可以看成從M映到K上的一個集值映射，并且Φ(u)≠0，?u∈M。

定理2 Φ:M?K是usco映射。

證明由于 K是緊集，故只需證 Graph(Φ)是 M×K的閉子集，這里 Graph(Φ)={((S，T，η)，x)∈M ×K:x∈Φ(S，T，η)}。因為M是完備的，K是緊集，故M×K是完備的。所以可證任取序列 {((Sn，Tn，ηn)，xn)}?Graph(Φ)滿足((Sn，Tn，ηn)，xn)→((S，T，η)，x)∈M ×K。

因為 xn∈ Φ (Sn，Tn，ηn)，則有，xn∈ Sn(xn)且存在 tn∈ Tn(xn)，滿足 [ tn，ηn(y，xn)]? －intC，?y∈Sn(xn)。

任取 L(X，Y)中 的 開 集 O? T(x*)，因 為 T(x*)是 緊 集，存 在 ε0＞0使{ξ∈L(X，Y):d(ξ，T(x*))＜ε0}?O。由于 ρ((Sn，Tn，ηn)，(S，T，η))→0，xn→x*，T 在 x*點是上半連續的，所 以 ?N，使 當 n ＞N 時，有且 T(xn)?這樣，當 n＞N 時，有{ξ∈L(X，Y):d(ξ，T(x*))＜ε0}?O。因tn∈Tn(xn)，由引理2知，存在 {tn}的一個子列 { tnp}?L(X，Y)，使tnp→t*∈T(x*)，不失一般性，可設tn→t*。

因 xn∈Sn(xn)，ρ((Sn，Tn，ηn)，(S，T，η))→0，xn→x*，且 Sn是連續的因而上半連續的，所以類似地可以證明:存在 { xn}的一個收斂子列 { xnp}，使得 xnp→x0∈S(x*)。由于 xn→x*，可知 x0=x*∈S(x*)。

又由于 S 在 x*下半連續，?z∈S(x*)，存在 yn∈S(xn)，使得 yn→z。再由 ρ((Sn，Tn，ηn)，(S，T，η))→0 可知?p∈N，?np使得取 { xn}的子列 { xnp}，有 h1(Snp(xnp)，S(xnp))＜1/p，于是存在y'np∈Snp(xnp)，使得‖y'np－ynp‖ ＜ 1/p，那么就有‖y'np－z‖≤‖y'np－y'np‖ +‖z－ynp‖ ＜1/p+‖z－ynp‖，而 ynp→z，故有 y'np→z。

又因為 ρ((Sn，Tn，ηn)，(S，T，η))→0，則對于?(x，y)∈K ×K 有 ηn(x，y)→η(x，y)，且 η 是連續的，則 η(y'np，xnp)→η(z，x*)。所以有 ηn(y'np，xnp)= ［ηn(y'np，xnp)－ η(y'np，xnp)］+［η(y'np，xnp)－η(z，x*)］+ η(z，x*)→η(z，x*)。

又由于之前得到了 y'np∈Snp(xnp)，且 xnp∈Snp(xnp)，tnp∈Tnp(xnp)，所以有

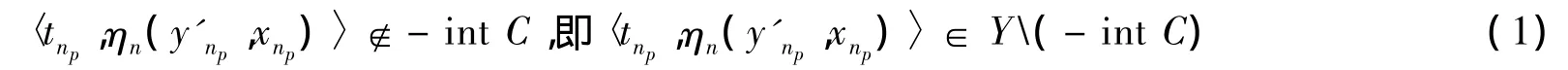
其中Y(－intC)是閉集。對式(1)兩邊同時取極限得到〈t*，η(z，x*)〉∈Y(－intC)，即〈t*，η(z，x*)〉?－intC，由 z在 S(x*)中任意性以及 x*∈S(x*)，t*∈T(x*)知 x*∈Φ(S，T，η)，即((S，T，η)，x*)∈Graph(Φ)，從而Graph(Φ)是閉集。由于K是緊集，從而Φ是緊值映射，所以Φ是usco映射。

引理4 如果Φ:M?K是usco映射，那么Φ在M的剩余集上是下半連續的。

定義2 對任意u∈M，x∈Φ(u):①稱x為u的本質解，若x在K中的任意開鄰域O，存在u在M中的開鄰域V，使對任意的u'∈V，有Φ(u')∩O≠?。②稱u為本質的，若u的每一個解都是本質的。稱u是弱本質的，若存在u的某個解是本質的。

引理5 u為本質的，當且僅當集值映射Φ在u上是下半連續的。

定理3 存在M中的稠密剩余集Q，使對任意的u∈Q，u是本質的。

例1設E=X=Y=(－∞，+∞)，K=［－1，1］，C=R+=x:x≥{}0，考慮如下的GVQVLI:設T(x)={}θ，?x∈K，其中θ表示零算子;S(x)=K，?x∈K;η(x，y)=x－y，?x，y∈K。顯然u=(S，T，η)∈M，Φ(u)=K。

構造CVQVLI問題的函數序列 un=(Sn，Tn，ηn)∈M 如下:設 Sn(x)=K，?x∈K;Tn(x)=易驗證 ρ(un，u)→0，〈Tn(x)，ηn(x，y)〉=，所以根據定義2知，u即不是本質的也不是弱本質的。

例1表明，定理3中Q≠M，M中的某些問題元素u所決定的GVQVLI的解集甚至不存在本質解。

3 GVQVLI解集的本質連通區的存在性

在這一部分中設η0:K×K→E取定，滿足η0是連續的，固定x∈K，η0(·，x)是仿射的，若x∈intS(x)，則 η0(x，x)=0。令

由例1知，雖然M中有些元素u所決定的GVQVLI不存在本質解，但可以證明，?u∈M由u所決定的GVQVLI解集至少存在一個本質連通解集，此時，?u∈M，Φ(u)是K中的緊集。

設u∈M，x∈Φ(u)，Φ(u)中包含x的所有的連通子集的并集稱為Φ(u)的一個連通區，Φ(u)的連通區是Φ(u)的連通閉子集，從而是連通的緊子集。Φ(u)中分別包含相異兩點的連通區，要么是重合的，要么是不相交的，故Φ(u)被分解為一簇兩兩不相交的連通區的并集，即Φ(u)有如下的連通區分解:，其中 Λ 為一指標集，對?α∈Λ，Φα(u)為一非空連通緊子集，且對?α，β∈Λ，α≠β，有Φα(u)∩Φβ(u)=?。

定義3 對?u∈M，設G是其解Φ(u)的非空閉子集，稱G為Φ(u)的本質集，若對包含G的K中任意開集O，即存在δ＞0，使得對任意滿足ρ(u，u')＜δ的u'，有Φ(u')∩O≠?。若Φα(u)為Φ(u)的本質集，則稱Φα(u)為Φ(u)的本質連通區。Φ(u)的一個本質集G稱為極小本質集，若G在Φ(u)的所有本質集的族中按包含關系所定的序關系是極小元。

引理6 設A、B、C是賦范向量空間 E的非空有界凸子集，那么 h(A，λB+μC)≤λh(A，B)+μh(A，C)，其中 h表示的是 Hausdorff距離，λ≥0，μ≥0且 λ +μ=1。

定理4 對任意的u∈M，Φ(u)至少存在一個極小本質集。

證明由定理2知Φ是上半連續的，由上半連續的定義及定義3知Φ(u)本身就是一個本質集。記Ψ為Φ(u)的所有本質集全體，則(按包含關系定序)Ψ非空。對Ψ的任一非空全序子集φ，由于φ的每個成員都是緊的，故φ中所有成員之交仍為緊集，因而φ有下界。于是由Zorn引理可知φ有極小元，這個極小元就是Φ(u)的一個極小本質集。

定理5 對每一個u=(S，T，η0)∈M，Φ(u)的每一個極小本質集都是連通的。

證明設m(u)是Φ(u)的極小本質集，若m(u)不是連通的，則存在Φ(u)的2個非空閉子集c1(u)和 c2(u)以及K 中2 個開集V1、V2，使得m(u)=c1(u)∪c2(u)，c1(u)?V1，c2(u)?V2，V1∩V2= ?。由于m(u)是Φ(u)的極小本質集，故c1(u)和c2(u)都不是本質的。于是存在K中開集O1?c1(u)，O2?c2(u)，使對任意的 δ＞0，存在 u1，u2∈M，從而

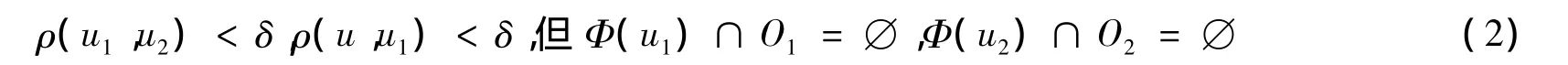
記 W1=V1∩O1，W2=V2∩O2，則 W1、W2都是開集，且滿足 W1?c1(u)，W2?c2(u)，W1∩W2= ?。因為Φ(u)是緊集，因而 c1(u)和 c2(u)是緊集。故存在 2個開集 U1、U2，使得，其中表示 U1在K 中的閉包。由于U1∪U2?m(u)以及 m(u)以及m(u)是本質集，存在 δ'＞0，使對任意滿足 ρ(u，u')＜ δ'的 u'，有

又由于 U1?O1，U2?O2，對 δ'/2 ＞0，由式(2)知存在 u1，u2∈M，使得

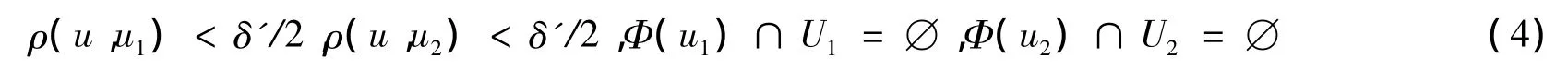
記 u1=(S1，T1，η0)，u2=(S2，T2，η0)，現構造一個 u'=(S'，T'，η0)如下:

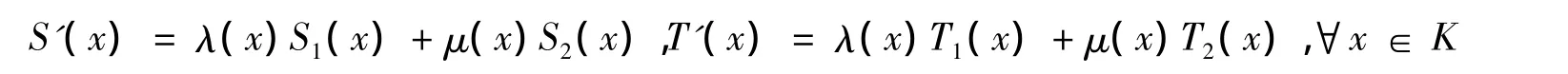
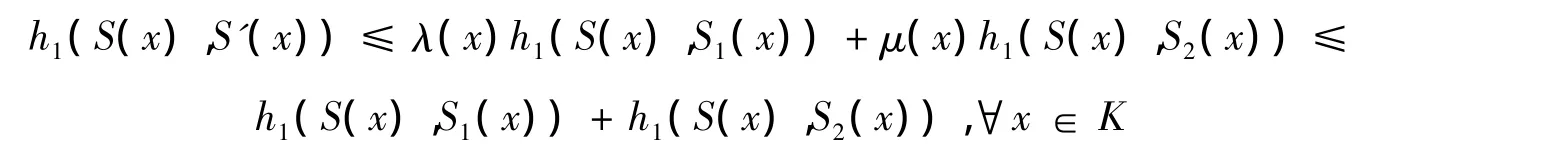
且

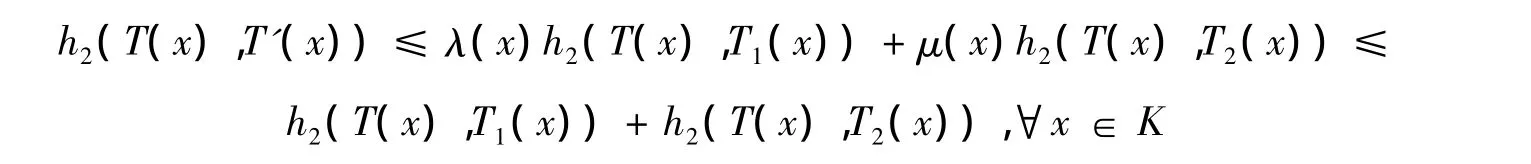
所以，根據式(4)有

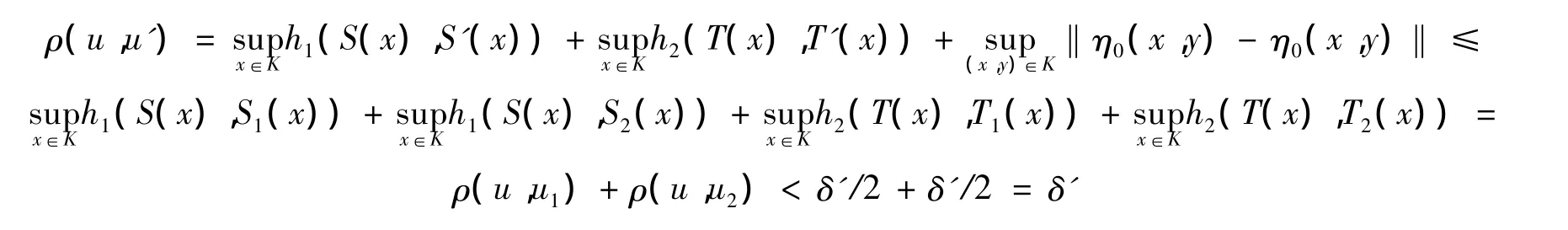
再由式(3)得

但是由 u'的構造又有如下事實:設 x∈U1，則當 λ(x)=1，μ(x)=0時，有 S'(x)=S1(x)，T'(x)=T1(x);若 x∈Φ(u')，則 x∈S'(x)=S1(x)，且存在 t∈T'(x)=T1(x)，使得〈t，η0(y，x)〉? － intC，對于任意的y∈S'(x)=S1(x)。于是x∈Φ(u1)，這與式(4)矛盾。故Φ(u')∩U1=?。同理可證Φ(u')∩U2=?。所以Φ(u')∩(U1∪U2)=?，這與式(5)矛盾，因此m(u)必是連通的。

定理6 對每一u∈M，Φ(u)中至少存在一個本質連通區。

證明由定理4、5知，Φ(u)中至少存在一個連通的極小本質集G，而G必包含于Φ(u)的連通區Φα(u)，因為G是本質的，由定義可知Φα(u)就是Φ(u)的本質連通區。

定理7 若u∈M使得Φ(u)僅由孤立點組成，則u是弱本質的，特別的，若Φ(u)是單點集，則u必是本質的。

4 本質連通區的連續性

已知(M，ρ)是一個可測空間，而(K，d)是緊的可測空間。對于任意的 ε＞0，x∈K，A?M，記O(x，ε)= {u∈M:ρ(x，u)＜ε }，U(ε，A)= {y∈K:?u∈A，使得 d(u，y)＜ ε}，B(ε，A)={y∈K:?u∈A，使得 d(u，y)≤ε}。顯然，U(ε，A)是開集，而當A是緊集時B(ε，A)是閉集。

定理8 對于任意的u∈M，如果m(u)是Φ(u)的最小本質集，那么對于任意的ε＞0，?δ＞0，使得對于任意 u'∈M，若滿足 ρ(u，u')＜δ，則存在 Φ(u')的最小本質集 m(u')，并且有m(u')?B(ε，m(u))。

證明假設結論不成立，即存在ε0＞0，使得對任意的δ＞0，都存在u'∈M，ρ(u，u')＜δ滿足m(u')?B(ε0，m(u))，其中m(u')是Φ(u')中任意的最小本質集。

由于m(u)是 Φ(u)的本質集，則對以上的 ε0＞0，存在 δ0＞0，使得對任意的 u'∈M 且 ρ(u，u')＜ δ，有 U(ε0，m(u))∩Φ(u')≠?。

又因為 B(ε0，m(u))∩Φ(u')是 Φ(u')中的閉子集并且 B(ε0，m(u))∩Φ(u')?B(ε0，m(u))，再由假設知 m(u')?B(ε0，m(u))，所以 B(ε0，m(u))∩Φ(u')不是 Φ(u')的本質集。那么，存在 ε1＞0，使得對于任意的 δ＞0，存在 u″∈M，ρ(u'，u″)＜δ，但是 U(ε1，B(ε0，m(u))∩Φ(u'))∩Φ(u″)=?。

令 δ1，δ2，δ3，…是單調下降趨向于 0 的序列，使得 O(u'，δn)?O(u，δ0)。再取 un∈O(u'，δn)，滿足U(ε1，B(ε0，m(u))∩Φ(u'))∩Φ(un)=?。由于 ρ(u，un)＜ δ0，U(ε0，m(u))∩Φ(un)≠?，再令 yn∈U(ε0，m(u))∩Φ(un)，因為 K 是緊集，所以不失一般性，假設 yn→y0∈B(ε0，m(u))。又因為 xn→x'，yn∈Φ(xn)，yn→y0，且 Φ 是 usco 的，所以就有 y0∈Φ(u')。然而，yn∈Φ(un)，U(ε1，B(ε0，m(u))∩Φ(u'))∩Φ(un)=?，所以就有 yn?U(ε1，B(ε0，m(u))∩Φ(u'))。再由 yn→y0，就可以得到 y0?U(ε1/2，B(ε0，m(u))∩Φ(u'))，這與 y0∈B(ε0，m(u))∩Φ(u')矛盾。所以結論成立。

定理9 對于任意的u∈M，如果c(u)是Φ(u)的最小本質區，并且存在ε0＞0，使得B(ε0，c(u))∩B(ε0，Φ(u)c(u))=?，那么對任意的 ε ＞0，?δ＞0，使得對于任意 u'∈M，若滿足 ρ(u，u')＜ δ，則存在Φ(u')的最小本質區c(u')，并且有c(u')?B(ε，c(u))。

證明首先，存在Φ(u)的最小本質集m(u)，滿足m(u)?c(u)。再根據定理8，?ε＞0，?δ1＞0，使得?u'∈M，ρ(u，u')＜δ1，存在 Φ(u')的最小本質集 m(u')，滿足 m(u')?B(ε，m(u)?B(ε，c(u))。又有Φ(u')的一個區c(u')，滿足m(u')?c(u')，所以顯然c(u')是Φ(u')的一個本質區。

Φ在u處是上半連續的，所以存在 δ2＞0，使得對于任意的 u'∈M，ρ(u，u')＜δ2，有 Φ(u')?U(ε，Φ(u))?B(ε，c(u))∪B(ε，Φ(u)c(u))。下證 Φ(u)c(u)是閉集，故也是緊的。對于?yn∈Φ(u)c(u)，yn→y，有 yn∈Φ(u)，yn?c(u)。由于 Φ(u)是緊的，有 y∈Φ(u)。如果 y∈c(u)，則對于足夠大的 n，yn∈B(ε0，c(u))成立，但是這與 B(ε0，c(u))∩B(ε0，Φ(u)c(u))= ?矛盾，因此 y?c(u)，y∈Φ(u)c(u)，所以，Φ(u)c(u)是閉集因而是緊的。

令 δ=min{ δ1，δ2}，對于?u'∈M，ρ(u，u')＜ δ，若 c(u')?B(ε，c(u))，那么 c(u')∩B(ε，Φ(u)c(u))≠?且 c(u')∩B(ε，Φ(u))≠φ(因為 m(u')是它們的子集)。注意到當 ε ＜ε0時，B(ε，c(u))∩B(ε，Φ(u)c(u))=?。由于 c(u)和 Φ(u)c(u)都是緊的，所以 B(ε，c(u))和 B(ε，Φ(u)c(u))都是閉集。也就是非空連通集c(u')與2個非空閉集相交，不可能成立。因此就有結論c(u')?B(ε，c(u))。

備注2 如果Φ(u)是連通的，即Φ(u)的唯一本質區就是它自己，那么由于Φ是上半連續的，則對于?ε＞0，?δ＞0，使得?u'∈M，ρ(u，u')＜ δ，有，因此，對于 Φ(u')的任一本質區 c(u')，有 c(u')?Φ(u')?B(ε，Φ(u))成立。

［1］Fort M K.Essential and nonessential fixed points［J］.Am J Math，1950，72:315 －322.

［2］Kinoshita S.On essential components of the set of fixed points［J］.Osaka J Math，1952，4:19 －22.

［3］Wu W J，Jiang J H.Essential equilibrium points of n-person non-cooperative games［J］.Sci Sinica，1962，11:1307 －1322.

［4］Jiang J H.Essential components of the set of fixed points of the multivalued mappings and its applications to the theory of games［J］.Sci Sinica，1963，12:951 －964.

［5］Kohlberg E，Mertens J F.On the strategic stability of equilibria［J］.Econometrica，1963，54:1003 －1037.

［6］Hillas J.On the definition of the strategic stability of equilibria［J］.Econometrica，1990，58:1365 －1390.

［7］Yu J，Luo Qun.On Essential Components of the Solution Set of Generalized Games［J］.J Math Anal And Appl，1999，230:303－310.

［8］羅群，鄧曉紅，孫天翔.廣義向量似變分不等式解集的通有穩定性及本質連通區的存在性［J］.系統科學與數學，2002，22(1):90－95.

［9］Chen J C，Gong X H.The Stability of Set of Solutions for Symmetric Vector Quasi-Equilibrium Problems［J］.J Optim Theory Appl，2008，136:359 －374.