模糊控制在直線感應電機磁場定向控制中的應用

張云紅， 曾成碧， 徐 偉， 肖先勇

(1.四川大學電氣信息學院，四川成都 610065;

2.墨爾本皇家理工學院工程技術研究所，澳大利亞墨爾本 3001)

0 引言

單邊直線電機(以下簡稱“直線電機”)軌道交通系統作為一種新興的城市運輸方式，從20世紀80年代起，已經應用于許多城市的軌道交通系統中，比如加拿大溫哥華、日本東京、美國底特律、馬來西亞吉隆坡以及中國的廣州和北京等［1-2］。目前直線電機在各高校和企業都成為研究的熱點。直線電機驅動系統結構簡單，不靠輪和軌之間的摩擦力，而是直接依賴初次級間電磁感應原理所產生的水平推力，因此該系統具有很好的加減速性能和較強的爬坡能力［3-4］。但由于它相當于旋轉電機沿半徑中軸切開并水平展開，在其運行時，會產生縱向邊緣效應，引起氣隙有效磁通和牽引力系數降低［5］。所以直線電機的數學模型雖由旋轉電機而來，但比其更加復雜。本文引用J.Duncan［6-8］提出的直線電機數學模型，它考慮了電機的縱向邊緣效應，與實際情況相符。在此基礎上，建立了直線電機轉子磁場定向控制的仿真模型。傳統PI控制器算法簡單，穩定性高。但其基于線性系統設計，且參數固定，對于參數不斷變化的直線電機，其控制性能會大打折扣［9］。模糊控制不依賴于控制對象的數學模型，能夠模仿人的思維且將人的經驗帶入控制過程中［10-11］。文中將PI控制和模糊控制結合起來，設計了模糊自適應PI控制器，它能根據外部的變化，及時調節PI控制器的比例系數(KP)和積分系數(KI)，使其適應外部環境。將此控制器用在仿真模型的速度環中。仿真結果表明，模糊自適應PI控制器能夠克服控制系統的參數變化和非線性等因素，使其具有更快的速度跟蹤能力，更強的抗擾性和更好的魯棒性。

1 直線電機次級(轉子)磁場定向控制原理

1.1 直線電機數學模型

根據旋轉電機理論，本文建立了在次級磁場定向同步坐標系下的直線電機數學模型，主要總結如下［12］。

初次級電壓方程:

初次級磁鏈方程:

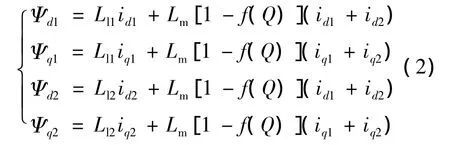
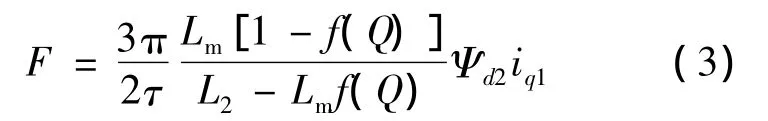
上述方程中的f(Q)為邊緣效應量化函數，其表達式如下:

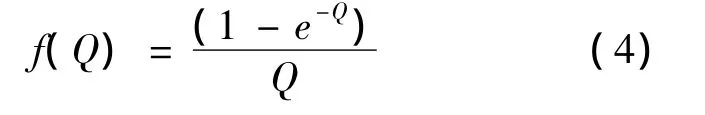
電機推力方程:

其中:ud1，uq1——分別為 d、q 軸初級電壓;

Ψd1，Ψq1——分別為 d、q軸初級磁鏈;

Ψd2，Ψq2——分別為 d、q軸次級磁鏈;

ω1——同步角頻率;

ω2——運動電角速度;

R1、R2——分別為初、次級電阻;

id1、iq1——分別為 d、q 軸初級電流;

Tv——初級通過空間一點的時間;

T2——渦流的衰減時間常數;

D——電機初級長度;v——電機線速度;ωsl——滑差頻率。

1.2 磁場定向控制原理

磁場定向分為氣隙磁場、定子磁場和轉子磁場定向。由于氣隙磁場和定子磁場定向控制方式復雜，本文采用轉子磁場定向控制。

滑差頻率方程:id2、iq2——分別為 d、q 軸次級電流;Lm——勵磁電感;

Ll1、Ll2——分別為初、次級漏感;

τ——初級極距;

L2——次級自感;

p——微分算子;轉子磁鏈角度方程:

次級磁鏈方程:

2 仿真模型介紹

在MATLAB/Simulink中建立的直線感應電機磁場定向控制結構如圖1所示。該模型包含一個速度控制的外閉環和兩個初級電流控制的內閉環。外閉環采用模糊自適應PI控制器，兩個內閉環采用PI控制器。逆變器采用SVPWM算法，直線感應電機的模型基于J.Duncan的數學模型。

PI控制是一種成熟的控制方法，并廣泛應用于工業控制系統中，其控制原理如圖2所示。比例調節能夠按比例反應系統偏差，一旦系統出現偏差，它將立即作用以減少偏差。比例系數大，能夠減少調節時間，但過大會降低系統穩定性，甚至造成系統不穩定。積分調節的目的是消除系統穩態誤差。只要系統存在穩態誤差，積分作用就一直進行，直至誤差消除。積分系數越小，積分作用就越強。但引入積分調節使系統穩定性下降，動態響應變慢。

圖1 直線電機磁場定向控制結構圖

圖2 PI控制器結構圖

文中結合PI控制和模糊控制設計的模糊自適應PI控制器結構如圖3所示。該控制器是一個雙輸入雙輸出的系統。輸入為運動電角速度誤差(e)和其誤差變化率(ec)，輸出為ΔKP和ΔKI。

圖3 模糊自適應PI控制器結構圖

該控制器通過模糊控制器的輸出ΔKP和ΔKI調節PI控制器的比例系數和積分系數，可表述為

式中，K'P和K'I為調整后的KP和KI。

模糊控制器的整個控制過程包括三個部分:輸入模糊化、模糊推理和輸出反模糊化，如圖4所示。

(1)輸入模糊化。如圖4所示，E和EC為輸入e和ec的模糊變量。設輸入和輸出的論域均為{－6，－5，－ 4，－ 3，－ 2，－ 1，0，1，2，3，4，5，6}。量化因子Ke和Kc用于模糊化輸入變量，如式(10)所示:

(2)模糊推理。定義模糊集合為{NB，NM，NS，Z，PS，PM，PB}，其隸屬度函數如圖 5 所示。NB和PB的隸屬度函數分別為Z型隸屬度函數，其余為三角形隸屬度函數。

圖5 輸入輸出的隸屬度函數

專家建議或經驗在模糊控制系統中被轉換為控制規則。根據輸入的模糊集合，該模糊控制器的輸出均有49條控制規則，如表1和表2所示，且采用Mamdani模糊推理方法。Kp和KI的輸出表面如圖6和圖7所示。

(3)輸出反模糊化。Kp和KI為ΔKP和 ΔKI的模糊變量。ΔKP和ΔKI為系統輸出的精確控制量。y1和y2為比例因子。反模糊化可描述為

表1 Kp的控制規則

表2 KI的控制規則

圖6 Kp的輸出表面

3 仿真結果和分析

模糊自適應 PI控制器的主要參數:Kp=0.06，KI=1，y1=0.1，y2=0.5。直線電機的主要參數如表3所示。

圖7 Ki的輸出表面

表3 直線感應電機主要參數

為比較PI控制器和模糊自適應PI控制器的性能，分別在兩種情況下進行仿真:(1)電機空載起動至線速度為5.6 m/s，并在第5 s時突然停止運動;(2)電機帶1 000 N負載起動至線速度為5.6 m/s，并在第5 s時突然停止運動。為簡化分析，該仿真忽略空氣和輪軌間等一切形式的摩擦力。

通過空載和帶負載的直線電機線速度曲線可看出，在速度環采用模糊自適應PI控制器的直線電機控制系統中，電機起動時線速度能較快達到設定值(空載時，采用模糊自適應PI控制器和PI控制器的系統上升時間分別為 0.105 s和0.118 s;帶負載時，分別為0.12 s和 0.127 s)，說明該控制系統具有較好的跟隨性能;電機制動時能較快停止且未出現超調和穩態誤差。這是因為空載起動和突然制動相當于速度發生了突變，在模糊自適應PI控制器的調節下，速度環可以根據速度反饋量的變化大小和快慢，實時地修正其比例系數和積分系數，使其適應外界的變化，從而系統具有更好的抗擾性和魯棒性，具體如圖8和圖9所示。

圖8 空載時直線電機仿真圖形

在兩種工況下，電機推力在傳統PI和自適應PI的調節下，其最后的變化曲線幾乎重合。這是因為對于推力控制，電流采取了限流措施，以防止電機燒壞。在飽和的狀態下，采用模糊自適應PI控制器的控制系統和采用PI控制器的控制系統的輸出是一樣的，都為電流限幅的上限;推力電流都采用相同的PI控制器，所以輸出的推力電流相同，因此輸出的推力也一樣。勵磁電感的曲線驗證了勵磁電感隨電機速度的上升而逐漸衰減。

圖9 帶1 000 N負載時直線電機仿真圖形

4 結語

本文結合PI控制和模糊控制的優點，設計了一種模糊自適應PI控制器，將其應用在直線電機轉子磁場定向控制的速度環中。其中根據 J.Duncan對邊端效應的直線電機互感的校正系數，本文利用MATLAB/Simulink中的模糊邏輯工具箱建立了模糊自適應PI控制器的仿真模型，并分別在空載和帶載的情況下進行了仿真研究，并與傳統的PI控制策略進行了對比。大量仿真結果表明:采用模糊自適應PI控制器的控制系統具有較好的跟隨性能、抗擾性和魯棒性。

［1］徐偉，李耀華，孫廣生，等.交通用大功率直線異步電動機牽引特性［J］.電工技術學報，2008，23(7):14-20.

［2］王珂，史黎明，何晉偉，等.單邊直線感應電機法向力牽引力解耦控制［J］.中國電機工程學報，2009，29(6):100-104.

［3］楊偉民，徐月同，陸華才，等.基于DSP的永磁同步直線電機無位置傳感器控制系統［J］.電機與控制應用，2007，34(4):28-32.

［4］任晉旗，李耀華，王珂.直線異步電動機的損耗模型與效率優化控制［J］.電工技術學報，2009，24(12):68-73.

［5］潘霞遠，劉希喆，吳捷，等.永磁同步直線電機的魯棒PID控制［J］.電機與控制應用，2008，35(9):34-38.

［6］DUNCAN J，ENG C.Linear induction motor-equivalent-circuit model［J］.IEE Proceeding of Electrical Power Application，1983，130(1):51-57.

［7］W X，ZHU J G.An improved equivalent circuit model of a single-sided linear induction motor［J］.IEEE Transactions on Vehicular Technology，2010，59(5):2277-2289.

［8］W X，ZHU J G.Equivalent circuits for single-sided linear induction motors［J］.IEEE Trans Ind Appl，2010，46(6):2410-2423.

［9］TURSINI M，PARASILITI F，ZHANG D Q.Realtime gain tuning of PI controllers for high-performance PMSM drives［J］.IEEE Trans Appl，2002，38(4):1018-1026.

［10］葉云岳，陸凱元.直線電機的PID控制與模糊控制［J］.電工技術學報，2001，16(3):11-15.

［11］WAI R J，CHU C C.Motion control of linear induction motor via Petri fuzzy neural network［J］.IEEE Trans Ind Electron，2007，54(1):281-295.

［12］任晉旗，李耀華，徐偉，等.直線感應電機在線參數辨識［J］.中國電機工程學報，2008，28(24):113-117.