新一代視頻編碼標準HEVC變換方法的研究
劉梅鋒,陸 玲
(東華理工大學機械與電子工程學院,江西 撫州 344000)
隨著眾多如數字電視、互聯網高清視頻、數碼相機、數碼攝像機等高清數碼產品的逐漸普及,現有的視頻編解碼標準已經不能滿足要求,尤其對于有著平滑背景的高分辨力視頻。因此,人們越發關注能適應高清甚至超高清視頻的高性能視頻編碼標準的開發進程。近期,ISO-IEC/MPEG和ITU-T/VCEG兩大國際標注化組織成立了視頻編碼聯合開發小組(JCT-VC),其目標是開發新一代國際視頻標準,名稱為高性能視頻編碼標準。該標準的目標是在保持H.264/AVC標準視頻質量的基礎上,使比特率降低一半,即壓縮率提高一倍。據HEVC參考軟件HM仿真結果顯示,目前針對HEVC標準提出的各個提案還未達到壓縮率提升一半的目標。與H.264/AVC視頻標準一樣,HEVC也包含幀內預測、幀間預測、運動估計與補償、正交變換、量化、濾波、熵編碼和重建等編解碼流程。
HEVC定義了3種類型的單元,包括編碼單元(CU)、預測單元(PU)和變換單元(TU)[1]。對于1個編碼單元,1幅圖像可以被分為多個片,而1個片可以被分為多個最大編碼單元(LCU),1個最大編碼單元又可以分為4個編碼單元,每個分片的編碼單元可以繼續分片至最大深度。HEVC定義了5種尺寸類型的編碼單元:128×128(LCU),64×64,32×32,16×16和8×8。預測單元被定義為編碼單元的支節點,因此,其尺寸最大不超過相應編碼單元的尺寸。而變換單元,則是針對正交變換和量化。對于幀內預測,HEVC定義了34幀內預測方向,遠遠超過了H.264/AVC 標準的9種[2]。除了傳統的16×16,8×8和4×4等尺寸外,還定義了8×2和2×8尺寸的長方形塊。對于幀間預測,HEVC采取了運動向量方案(MVR)、差值濾波(IF)、運動共享(MS)、運動向量競爭(MVC)和基于塊的照明競爭(B-BIC)來提高編碼性能。對于正交變換,HEVC采用包含了16×16,32×32和64×64等尺寸塊的變換矩陣、旋轉變換和基于模式的方向性變換來提高編碼性能[3]。對于濾波,HEVC采用了非線性降噪聲濾波(NDF)、幀自適應降噪聲濾波(ADF)、去方塊濾波(DBF)等濾波方法。對于熵編碼,HEVC采用了零樹編碼、基于語法的內容自適應二進制算術編碼(SB-CABAC)和自適應系數掃描來提高熵編碼的編碼性能。
本文試圖對最近6個JCT-VC會議中關于HEVC正交變換的若干主要提案進行研究討論,基于HEVC參考軟件模擬仿真結果,比較其各方面的性能優劣,最終提出HEVC正交變換的未來研究方向及可提升性能的研究點。
1 HEVC整數變換算法
截止到目前,HEVC標準中包含以下5種正交變換方法:基于模式的方向變換(MDDT)[4]、自適應DCT/DST選擇[5]、旋轉變換(ROT)[6]、IDCT 修剪和變換跳過模式(TSM)。
1.1 基于模式的方向變換(MDDT)
在視頻編碼正交變換的應用中,早已證實了Karhunen-Loève變換比DCT具有更高的性能。但在之前的H.264/AVC標準中,由于Karhunen-Loève變換實現較為復雜,而DCT具有如蝶形算法等快速的實現算法,因此被一直采用。
MDDT算法框架僅包含了1個DCT和1個派生的KLT,在MDDT中使用可分離變換來進行近似理想的非可分離方向變換。例如對于1個N×N像素的塊,其二維變換系數的計算公式為

式中:Cm和Rm的下綴m代表某預測方向上的行與列變換的依賴性。在H.264/AVC標準中,Cm=Rm=M,其中M是離散余弦變換DCT矩陣。在MDDT算法中,KLT采用Cm和Rm,而且是通過訓練視頻序列得到的預測模式m來計算預測殘差塊來完成的。
為了簡化派生過程,設每個圖像像素為零均值和單位方差的隨機變量。因此,該圖像像素的相關函數可定義為

因此幀內編碼后的殘差統計可以由式(2)得出。首先注意每個殘差行的統計特性,第k行(1≤k≤4)的方差矩陣為

接著,第k列(1≤k≤4)的相關矩陣可定義為

當N=4時,可以得到變換矩陣為


表1 HEVC中DCT/KLT的選擇
1.2 自適應DCT/DST選擇
三星公司提出了基于幀內預測模式判決的DCT/DST選擇算法。該算法不要求任何訓練,且不必準備大量的變換基,只要把一維的DCT和一維的DST類型7結合起來即可。當然上述結合只應用在幀內預測模式中。
由于DCT把能力集中在1個系數上,因此其視頻編碼性能較好。然而,在新的視頻標準中采用了眾多高效預測方法,從而導致DC系數能量的集中性也降低了。在此情況下,DCT在殘差信號的編碼中已經不適合了。另一方面,從能量集中的角度來看,DST反而適合這種信號的編碼。同時,DCT也不容易識別幅-頻特性和相-頻特性。且DCT的量化性能也影響信號的相位。兩種變換定義為

這些變換均包含三角函數,DST可以用DCT增加一些額外的變量來表示,DST中的正弦函數可以表示為
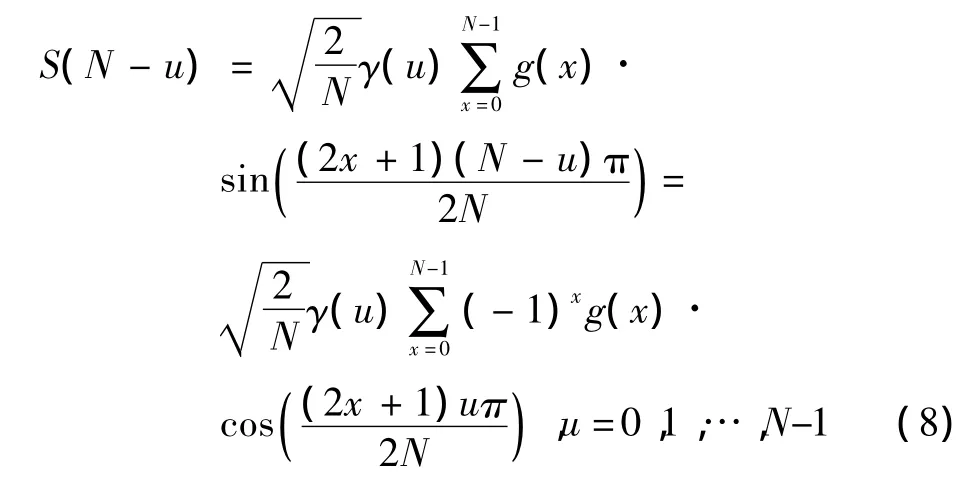
式(8)顯示了DST包含了DCT,而且有一半是與DCT相反的,這就意味著DST可以用一個DCT的電路來實現,如圖1所示。

圖1 4點DST和8點DST
其并行運算方法如圖2所示。

圖2 DST串行和并行處理的流程圖
在HEVC中DCT/DST選擇算法與幀內預測模式的對應關系如表2所示。
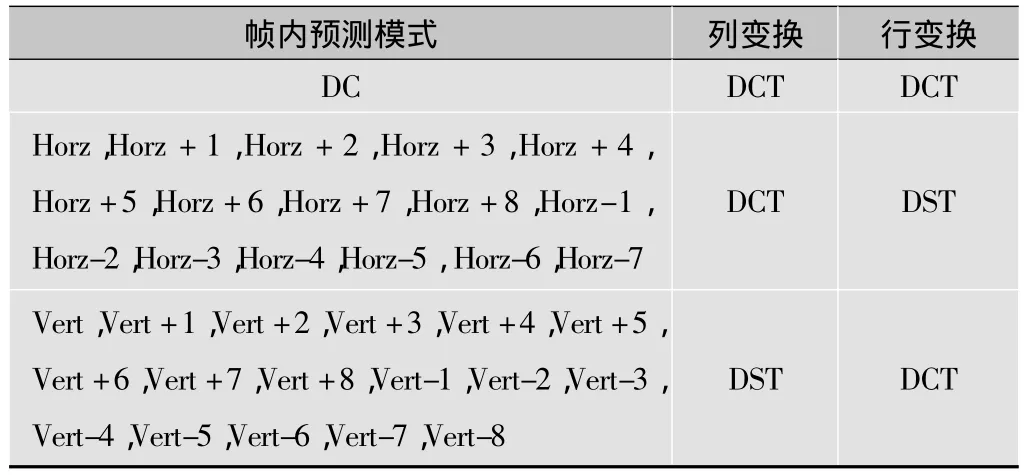
表2 HEVC中DCT/DST選擇算法
1.3 旋轉變換(ROT)
8×8旋轉變換(ROT)是DCT處理后的第二變換,該算法已嵌入到JCT-VC的HEVC測試軟件HM中了,其框架如圖3所示。

圖3 ROT應用于DCT之后
ROT變換塊mo計算公式為

式中:mi是輸入的殘差塊,D是DCT矩陣,Rh和Rv分別是水平和垂直的ROT矩陣,計算公式為

1.4 IDCT修剪
由于量化和正交變換的能力集中特性,大尺寸塊變換的高頻部分往往被量化為0。因此可以采用IDCT修剪算法來運行非零子塊信號,從而消除冗余的零入和零出IDCT計算量。提案中測量了各個非零子塊的發生率。令LK表示1個塊中最低頻子塊K×K為非零塊。16×16變換包括:L4,L8,L16;而32 ×32 變換包括:L4,L8,L16,L32。非零子塊百分比分布如表3所示。
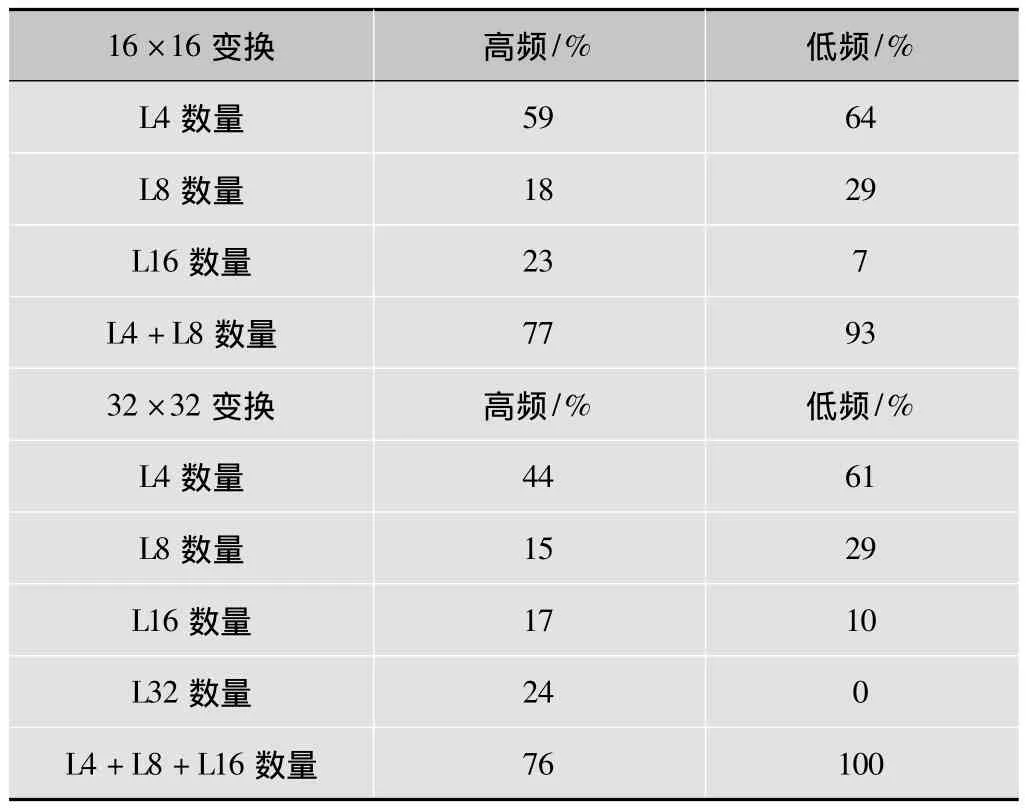
表3 非零子塊百分比分布
有的塊大部分均為0,而IDCT修建算法能有效地降低復雜度。1個N×N塊的二維IDCT需要2N個一維IDCT變換。比如,沿著行方向只需要執行N/2個變換,這種情況下總的變換數目僅需N/2+N=1.5N個,計算復雜度降低了25%。
總的變換數目將是:水平方向為N/2×N2/4;垂直方向為N×N2/4;總的數目為(3/8)×N2。
1.5 變換跳過模式(TSM)
在HM3.2中,其量化方法與H.264/AVC沒有改變,而在跳過變換的行/列處的縮放因子的選擇僅由塊的尺寸決定,基于率失真優化RDO搜索,編碼器為每個塊作一個變換/跳過的選擇,稱為變換跳過模式(TSM)。變換跳過模式信號被編碼傳送到解碼端,在解碼端也相應地作變換/跳過處理。此算法目前已經嵌入HM3.2中。
TSM決定一個或多個預測方向下變換是否跳過,在這些方向下變換將在普通條件下進行。這將于有利塊壓縮,例如在幀間預測的條件下,殘差塊信號之間的特征有很大不同。這些特征由很多因素決定,包括序列的運動程度和類型、量化步長和運動估計的精度等。對這種信號進行二維變換不是最好的方法,因為其強行用二維變換將現在DCT作為一種編碼工具的有效性。因此必須為TSM設計一種交替、低復雜度的方法。
變換/跳過模式如表4所示。處理模式TS0,該模式對應于二維變換,其余3種新的變換模式分別為:跳過垂直變換模式(TS1),跳過水平變換模式(TS2)以及水平、垂直均跳過變換模式(TS3)。在編碼器端一定要選擇4種情況中的1種,并且要把這個選擇編碼傳送到解碼器端。
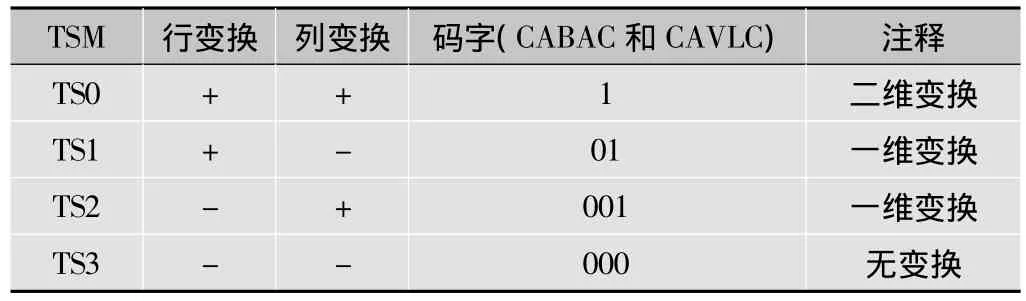
表4 TSM模式對于變換選擇和碼字
2 仿真結果分析
為了驗證前面介紹的幾種算法,筆者對各種算法進行了仿真實驗。
對于MDDT算法,本文采用KTA參考軟件(KTA2.6r1)。實驗中為幀內殘差塊采用4×4,8×8和16×16塊,并使用MDDT中提出的DCT與派生的KLT結合方法進行變換。對于16×16的塊,只應用到水平和垂直兩種方向上。在算法中,對于每種尺寸的塊變換只存儲2個變換矩陣。測試序列分別為BasketballDrive,BQTerrace,Cactus,Kimono1 and ParkScene。序列分辨力等級從A到E,測試目標為比特率的降低百分比和PSNR變化情況。仿真結果的平均值如表5所示。

表5 幀內預測下MDDT算法結果
據表5顯示,與傳統的DCT算法相比,MDDT算法獲得了7.75%的比特率下降,但與此同時PSNR視頻質量卻有一點提高。
對于DCT/DST,采用通用測試條件,幀內和幀間的8×8~32×32的TU都經過測試。變換類型是基于率失真優化結果來選擇的。DCT/DST算法的比特率和PSNR結果如表6所示。

表6 DCT/DST算法的比特率和PSNR結果
表6顯示了DCT/DST算法在HE模式下,比特率比原方法降低了0.1%~1.0%。當該算法應用在幀內預測的TU情況下,取得了較好的效果。另一方面,在AILC和RALC情況下該算法引起了比特率的升高,這是因為該算法必須為這些標志符號編碼并傳送到解碼器端。
對于ROT算法,仿真實驗采用了WQVGA,WVGA,720 p,1 080 p和4 k×2 k等規格的測試視頻序列。軟件版本為TMuC 0.9。操作系統為 Windows 7 Enterprise 64-bit,CPU 為 Inter Core(TM)i7,2.8 GHz。內 存 為4 Gbyte。測試結果如表7所示。

表7 ROT算法的比特率和編碼時間測試結果
目前,有許多人建議將ROT算法加入下一代HM參考軟件中去,但該算法引起的編碼時間上的增加卻不容忽視,尤其在幀內預測的情況下。
為了證明IDCT修剪算法,筆者比較了該算法與HM2.0的計算復雜度,結果如表8所示。

表8 IDCT修剪算法的計算復雜度
從表8可以看出,IDCT修剪方法比HM2.0無論在乘法還是加法上均有所減少。
TSM算法已經嵌入到HM3.2參考軟件中。該算法在幀間預測模式及ROT分離被關閉的情況下有效,而在幀內預測模式下則是無效的。
表9顯示了TSM算法在降低比特率的情況下提高了最大約為20%的計算復雜度。導致這種情況的原因是,在幀間預測的CU,TSM算法的每個選擇必須通過率失真來搜索,而該搜索需花費很多時間。

表9 IDCT修剪算法的比特率和編碼時間測試結果
3 未來研究方向分析
MDDT算法給HEVC帶來了較大的編碼性能提高,但同時也帶來了計算復雜度的增加。因此,如何降低該算法的計算復雜度將成為未來的一個研究方向。通過對這些計算范例的更具體細致的研究,將會帶來更低的計算復雜度。在幀內編碼的情況下,ROT算法帶來了編碼時間的增加。Loeffler因式分解被普遍認為有很好的穩定性,同時在加法和乘法方面的計算復雜度很低。但是它沒有很好地重復利用變換過程中已生效的小尺寸DCT類型2的變換。重復利用將在軟件和硬件編碼中大大降低計算復雜度。從以上的仿真結果來看,對于DST,如果能在比特率降低和計算復雜度之間設計更合理的折中方案,則將獲得更好的編碼性能。并行計算也將是HEVC標準的重要性能。然而,目前的標準中并沒有進行并行計算的處理。如果能在設計中采用并行計算的設計,則理論上其編碼時間將會降低一半。這個重要的特性就是在解碼器端增加一個額外的變換來降低解碼計算復雜度。研究基于模式的變換和掃描方法也是降低計算復雜度的一個方向。對于DCT/DST算法,采取更高效的變換矩陣是降低其復雜度的一個性能提高研究方向。最后,考慮到變換、量化后的信號更適應熵編碼,這也是一個間接降低比特率的重要研究方向。
4 總結
本文討論了HEVC視頻標準中幾種主要的正交變換算法。首先主要研究了基于模式的方向變換MDDT、自適應離散余弦/正弦變換(DCT/DST)、旋轉變換(ROT)、IDCT修剪和變換跳過模式(TSM)等方法。接著通過實驗仿真測試了這些算法在比特率的降低、編碼時間的縮短、軟硬件實現的復雜度和視頻質量等方面。最后,對HEVC正交變換方法方面提出了一些有待研究的重點和方向,以供視頻編碼研究工作者參考。
[1] HAN W J,MIN J H,KIM I K,et al.Improved video compression ef?ciency through flexible unit representation and corresponding extension of coding tools[J].IEEE Trans.Circuits Syst.Video Technol,2010,20(12):1709-1720.
[2] WIEGAND T.Joint collaborative team on video cFoding(JCT-VC)of ITU-T SG16 WP3 and ISO/IEC JTC1/SC29/WG11,JCTVC-B118.[S].[S.l.]:JCT-VC,2010.
[3] BOSSEN F,DRUGEON V,FRANCOIS E,et al.Video coding using a simpli?ed block structure and advanced coding techniques[J].IEEE Trans.Circuits Syst.Video Technol,2010,20(12):1667-1675.
[4] YEO C,TAN Y,LI Zhengguo.Mode-dependent fast separable klt for block-based intra coding[C]//Proc.IEEE International Symposium on Circuits and Systems(ISCAS),2011.[S.l.]:IEEE Press,2011:621-624.
[5] SAXENA A,FERNANDES F C.Jointly optimal intra prediction and adaptive primary transform[EB/OL].[2011-08-08].http://wftp3.itu.int/av-arch/jctvc-site/2010_10_C_Guangzhou/JCTVC -C108.doc.
[6] FERNANDES F C A.Low complexity rotational transform[EB/OL].[2011-08-09].http://wftp3.itu.int/av - arch/jctvc - site/2010_10_C_Guangzhou/JCTVC - C096.doc.

