一種基于位置誤差檢測門限的機動目標跟蹤算法＊

湯傳貴 張 珂 晁愛民 張國棟

（1.海軍駐青島造船廠軍事代表室 青島 266001）（2.海軍工程大學 武漢 430033）

1 引言

在現代跟蹤系統中，對勻速目標的跟蹤是很容易實現的，但對于機動目標的跟蹤就比較困難，原因在于很難建立精確的機動目標模型。研究人員做了大量的工作，提出了許多模型，其中周宏仁等人提出的機動目標“當前”統計模型［1］是目前較好的一種。由于這些模型自身的局限，單獨采用一個模型進行濾波精度不高。為此，Bar—Shalom和Blom等人在廣義偽貝葉斯算法的基礎上，提出了一種具有馬爾可夫切換系數的交互式多模型（IMM）濾波算法［2～3］，其中多個模型并行工作。模型間以概率矩陣進行轉移，目標狀態估計是多個濾波器交互作用的結果，該算法不需要機動檢測，達到了全面自適應的目的。

但是在實際的MM算法運行過程中，總模型集里僅僅只有一小部分模型對整體狀態的估計有較大作用。因此，在任何時刻都使用固定的模型集是不合適的，以上算法中的限制可以通過時變模型集的方法解決，這種方法被稱為變結構多模型（VSMM）算法，由 Li X R［4］和 Kirubarajan［5］等人所提出。VSMM算法可以看作是普通的定結構多模型算法（FSMM）加上一個利用當前時刻狀態調整使用模型的控制模塊。在VSMM算法的設計中，不僅需要像FSMM算法一樣考慮所有可能模型集合，還需要考慮在某一時刻如何選擇使用有效的模型集合，從而達到降低算法運算負荷的目的。

本文通過對位置誤差的檢測實現模型集合自適應，屬有向圖切換法。基于位置誤差檢測的VSMM算法與IMM算法的仿真實驗比較結果說明了該算法的有效性。

2 基于RAMS的VSMM算法簡介

理想的VSMM算法應該分成兩層結構，上一層為多模型集合序列，下一層為模型集合內的多模型序列，整體狀態估計由下式給出［6］：

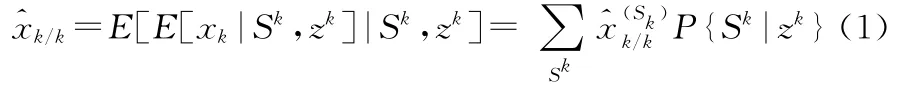
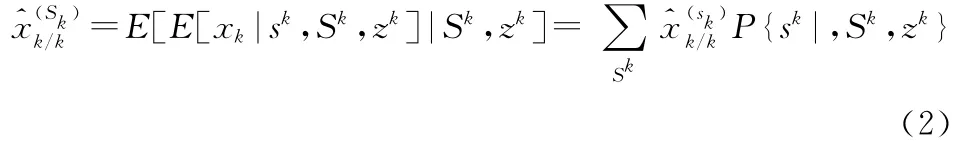
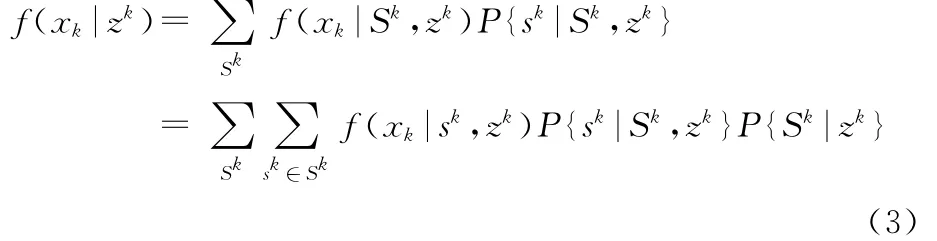
VSMM算法的兩級融合結構如圖1所示。

圖1 VSMM算法兩級融合結構示意圖

3 基于位置誤差檢測的VSMM算法

本文采用極坐標系下的量測模型和直角坐標系下的狀態模型進行目標跟蹤理論的研究。以我艦觀測雷達為原點建立空間直角坐標系，則目標在直角坐標系內的運動情況如圖2所示。

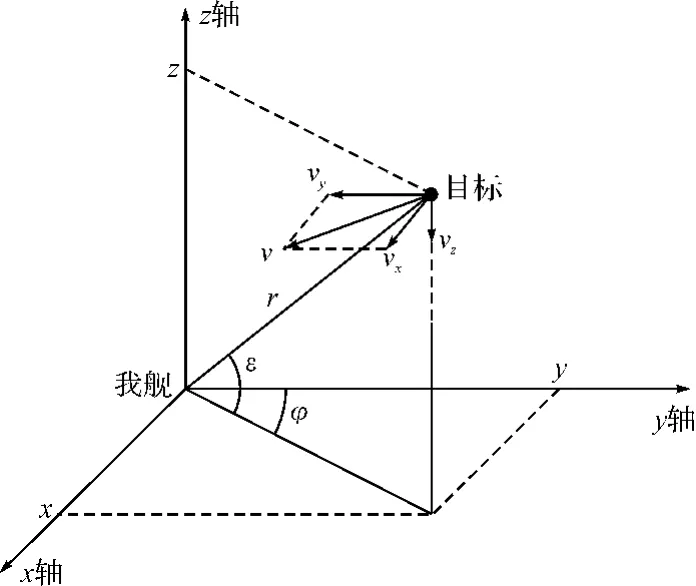
圖2 火控濾波直角坐標系及目標運動情況

參照圖2，假設目標在水平面內做勻速直線運動，r、φ、ε是觀測雷達輸出的斜距、方位角、俯仰角信息，設斜距、方位角、俯仰角的隨機觀測誤差均方差分別為σr、σφ、σε，同時忽略系統誤差。

由此可見，二甲雙胍能有效地延緩AS的進展，對T2DM患者心血管系統具有一定的保護作用。但由于受倫理道德原則、《藥物臨床試驗質量管理規范》（GCP）和相關法律法規的約束，目前該方面臨床研究還相對較少，其結論仍有待進一步驗證。

假設初始速度和位置為零，極坐標系與直角坐標系之間的關系如下：

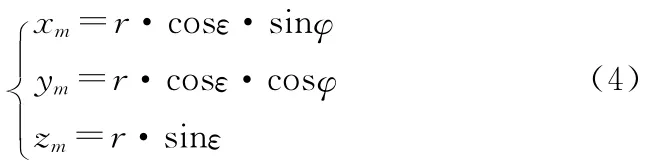
3.1 模型集合設計

由于目標作轉彎機動時除了位置和速度信息的變化外，還存在著高低角和方位角信息的變化，并且測量信息在三維直角坐標系下是相互耦合的，因此傳統VSMM算法對三維空間中目標的轉彎機動跟蹤效果較差，而對目標的勻速、勻加速機動跟蹤效果較好。基于以上原因，本文模型集的設定將主要針對目標的轉彎機動。設定以下6個模型集，模型集中包含各子模型：

模型集1：｛勻速直線運動目標（CV）跟蹤模型；勻加速直線運動目標（CA）跟蹤模型｝

模型集2～模型集6為不同高低角變化率的勻速圓周運動目標（CT）跟蹤模型組合，每一個模型集里面包含四個不同高低角變化率和方位角變化率的CT跟蹤模型。

上述模型集中，模型集1針對目標的直線運動，模型集2～6針對目標的曲線運動，各模型集中的子模型均為典型單目標跟蹤模型［8～9］。

3.2 機動檢測準則設計

采用滑窗式［7］檢測法，記當前時刻位置濾波誤差為D，檢測門限為m。當D＞m時，判定目標發生機動；當D＜m時，判定目標機動消除。

3.3 最佳模型集合選擇準則設計

若模型集1的IMM濾波結果符合機動檢測準則，則確定目標做直線運動，該集合為最佳模型集合；若模型集2～6中某一模型集的IMM濾波結果符合機動檢測準則，則確定目標做曲線運動，該集合為最佳模型集合。

3.4 VSMM算法流程

以觀測系統輸入的第一次觀測值為濾波器的初值，濾波器從k＝1開始工作。

2）算法描述

Step1：對VSMM進行初始化，輸入初值X1，P1；

Step2：對各模型集進行IMM濾波；

Step3：判斷出各模型集中新息殘差最小的模型集a，輸出模型集a的濾波結果；

Step4：更新量測值；

Step5：對模型集a進行IMM濾波，若濾波結果未檢測到目標機動，則輸出模型集a的濾波結果；若濾波結果檢測到目標機動，則激活其它模型集，并利用a在k－1時刻的結果對各模型集進行重新初始化；

Step6：是否停止解算？是，結束；否則，轉Step3。

流程圖如圖3所示。

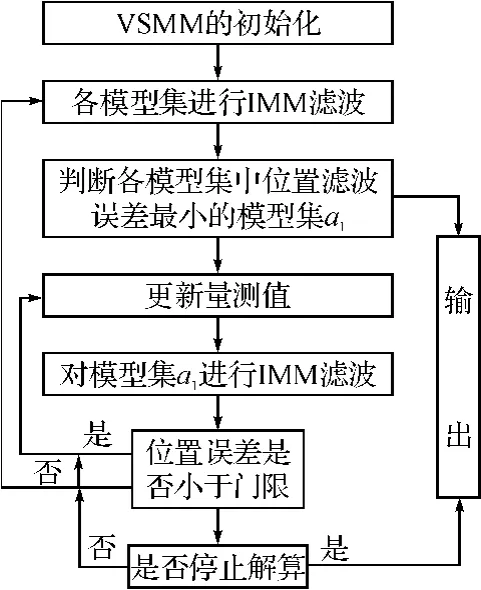
圖3 VSMM濾波算法流程圖

4 仿真實現

為了驗證本文所提算法的有效性，對本文算法與傳統IMM算法進行蒙特卡洛仿真實現，并對兩種算法的跟蹤性能進行比較分析。

4.1 仿真初始設定

設目標在三維空間內進行機動，前2s做速度為850m／s的勻速直線運動，2～6s做加速度100m／s的勻加速運動，6～10s做方位角速度0.2rad／s、高低角速度0.1rad／s的勻速轉彎運動：初始斜距11325m；雷達采樣率50Hz；采樣持續時間10s；觀測距離隨機誤差5m；觀測距變率隨機誤差2m／s；觀測方位角、高低角隨機誤差0.9mrad；觀測方位角、高低角變化率隨機誤差0.5mrad／s。

4.2 仿真結果

圖5～圖10顯示，對x、y軸位置信息來說，在目標尚未發生機動的0～2s，兩種濾波算法的效果相差不大，這是由于兩種算法采用同樣跟蹤子模型進行濾波的原因；但在目標機動發生后，VSMM算法的濾波效果要明顯好于IMM算法；對x、y軸速度信息來說，不論目標是否作機動，VSMM的濾波效果始終好于IMM；兩種算法對z軸位置信息和速度信息的濾波效果相差不大。這說明采用本文的機動檢測方法后，濾波算法對三維空間中作機動的目標跟蹤能力有了較明顯提高，但對于不作機動的目標而言，跟蹤效果改善并不明顯。

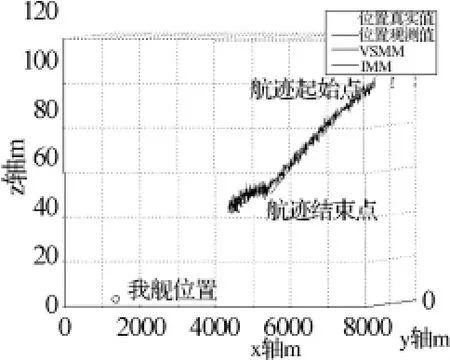
圖4 目標運動軌跡及兩種濾波模擬

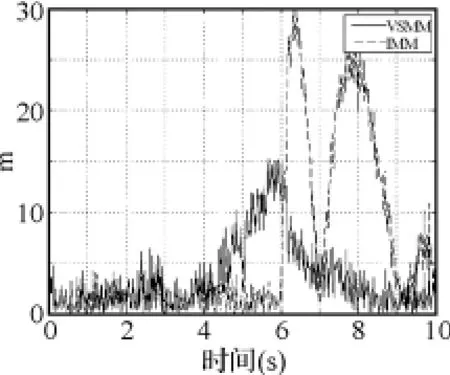
圖5 x方向的位置濾波誤差比較圖

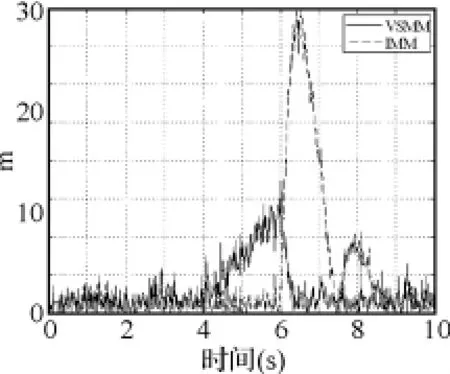
圖6 Y方向的位置濾波誤差比較圖

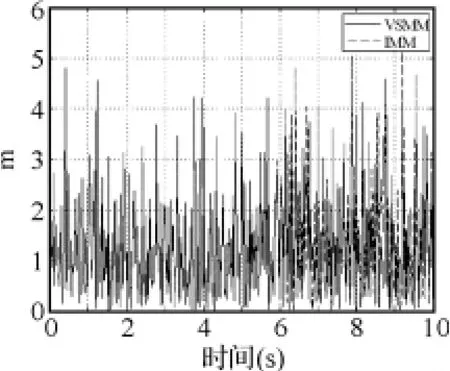
圖7 Z方向的位置濾波誤差比較圖

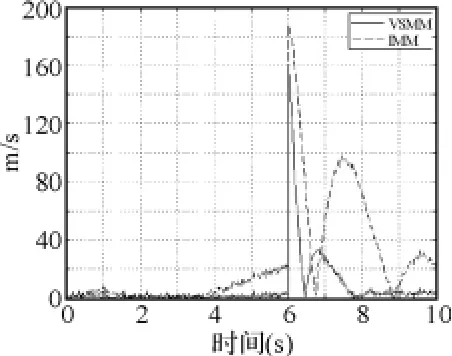
圖8 X方向的速度濾波誤差比較圖

5 結語

本文在分析典型多模型算法（IMM）不足的基礎上，通過改進現有變結構交互多模型算法（VSMM），將檢測門限設置為目標跟蹤位置誤差門限，根據對目標位置信息的誤差檢測來判定目標是否作機動。仿真實驗證明，該方法可有效提高多模型算法對三維空間機動目標的濾波效果，具有一定理論價值。

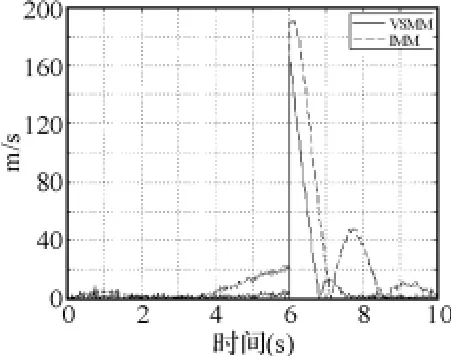
圖9 Y方向的速度濾波誤差比較圖

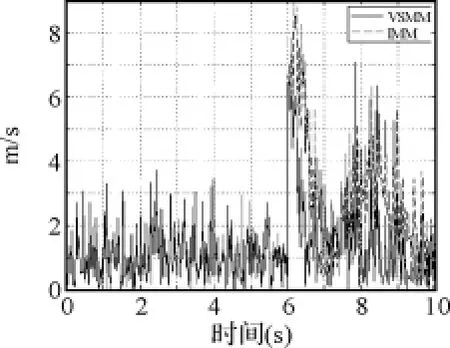
圖10 Z方向的速度濾波誤差比較圖

［1］周宏仁，敬忠良.機動目標跟蹤［M］.北京：國防工業出版社，1991：19-21，25，31-32.

［2］Blom H A，Bar-Shalom Y.The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients［J］.IEEE Trans.On Automatic Control，1988，33（8）：780-783.

［3］Mazor E，Averbuch A，Bar-Shalom Y，et al.Interacting Multiple Model Methods in Target Tracking：A Survey［J］.IEEE Trans.On Aerospace and Electronic Systems，1998，34（1）：103-123.

［4］LI X R，Bar-Shalom Y.Multiple Model Estimation with Variable Structure［J］.IEEE Transactions on Automatic Control，1996，24（1）：478-493.

［5］Kirubarajan T，Bar-Shalom Y，Pattipatik P，et al.Ground Target Tracking with Variable Structure IMM Estimator［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36（1）：26-44.

［6］A.T.Alouani，P.Xia，T.R..Rice，et al.Two-stage Kalman eastimator for tracking maneuvering targets［J］.Conf.Proc.1991IEEE International Conference on systems，Man，and Cybernetics.Decision Aiding for Complex Systems，1991（2）：761-766.

［7］范紅旗，王勝，付強.目標機動檢測算法綜述［J］.系統工程與電子技術，2009（5）：1064-1070.

［8］何友.雷達數據處理及應用［M］.北京：電子工業出版社，2005：132-137.

［9］石章松，周豐，孫世巖.目標跟蹤與數據融合理論及其應用［M］.武漢：海軍工程大學，2007：145-217.