基于當前統計模型的目標跟蹤改進算法仿真分析*

張安清，文 聰，鄭潤高

(海軍大連艦艇學院信息與通信工程系，遼寧 大連 116018)

0 引言

當前統計模型是目前在機動目標跟蹤模型中應用最廣泛的模型之一。它是用修正的瑞利分布來描述機動加速度的當前概率密度［1］，其均值為當前加速度的預測值，以實現對均值自適應濾波，同時又利用狀態噪聲方差與機動加速度方差的關系來完成對目標的方差自適應濾波。但是，在計算方差時需要預先設定加速度的極大值和極小值，在實際應用中存在很大不足，機動目標一旦真實加速度超過極限值，其跟蹤性能將迅速降低，且若采用的目標跟蹤模型與目標實際的運動模型不一致，會使系統的誤差變大，甚至有可能造成目標丟失。針對當前統計模型的這些不足，本文通過改變算法中的參數，自適應地調整加速度方差和機動頻率等，并仿真分析改進算法前后對不同機動情況的目標跟蹤效果，指出需自適應調整目標跟蹤算法的參數，使當前統計模型下的跟蹤算法更能夠精確跟蹤機動目標，發揮最佳效果。

1 當前統計模型的目標跟蹤

當前統計模型是采用機動加速度的非零均值時間相關模型。

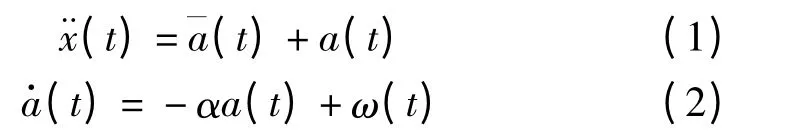
①當目標當前的加速度為正時:

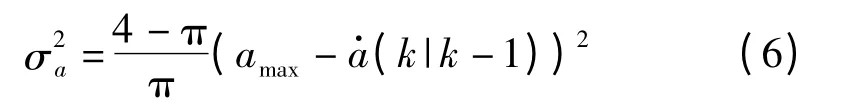
②當目標當前的加速度為負時:

2 參數自適應改變的當前統計模型算法

2.1 目標加速度方差的自適應調整

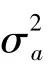
在采樣周期T 內，鑒于機動加速度方差與加速度的絕對值成線性關系，而加速度增量與位置增量之間也存在線性關系，因此可得到k時刻的加速度方差自適應調整為

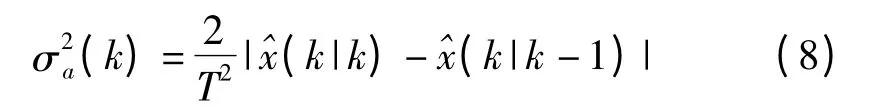
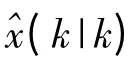
2.2 機動頻率α的自適應調整

在機動目標狀態估計中，由于機動目標模型一般都是非線性的，每一次濾波都會產生一個新的殘差，理論上該殘差符合零均值的正態分布。如果目標狀態發生突變，殘差會變大，其均方值會偏離理論值，若殘差特征出現偏離，認為目標的機動頻率α發生改變，應及時調整α 值。卡爾曼濾波殘差或新息為

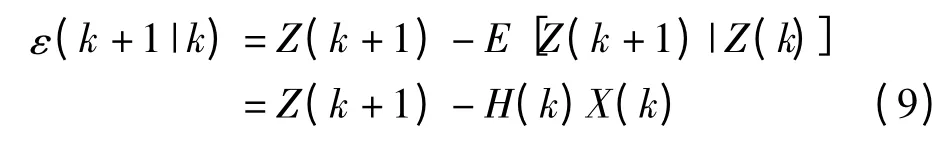
由卡爾曼濾波殘差ε(k），應用簡化的最小均方誤差(LMS）算法［5］對機動頻率α 進行調整，自適應調節公式為

其中μ為收斂系數，當調整收斂后，得到機動頻率α的值，從而根據濾波殘差來自適應地調整目標機動頻率α 值，實現對狀態轉移矩陣和狀態協方差矩陣的調整，使其更接近于目標的真實狀態。

3 仿真實驗

為簡便，對機動目標的其中一個方向上，分別應用加速度方差改進算法和機動頻率改進算法進行仿真，并與當前統計模型下的傳統非自適應算法進行比較，分析各自跟蹤性能。其次，根據改進算法自身的特性，優化調整影響跟蹤精度的參數，以期達到最佳效果。最后，指出3 種算法的最佳適用情況。

3.1 加速度方差自適應跟蹤算法仿真

設機動目標沿x 軸運動，初始位置x0=50000 m，初始飛行速度v0=150 m/s，0～50 s 勻速運動;50～100 s 慢加速運動，加速度為a1=5 m/s2;100～150 s目標勻速運動;150～180 s 目標做快減速的大機動，加速度為a2=60 m/s2;180～200 s 目標勻速運動;200～220 s，目標做中加速運動，加速度為a3=25 m/s2;220～250 s 目標勻速運動。狀態估計包括目標的位置、速度、加速度。觀測噪聲V(k）是均值為0、方差為1的白噪聲，測量誤差方差r=5000;采樣時間T=1 s，α 取0.9;amax=8*g，amin=－8*g，g=10。仿真結果如下:

圖1 加速度方差變化的跟蹤效果圖(150～180 s）

圖1所示為150～180 s時間段目標以較大的加速度作大機動仿真結果。圖2所示為200～250 s時間段內目標既有較小的加速運動也有勻速運動仿真結果。

表1為機動目標在各種變加速度情況下觀測噪聲隨機生成，每種情況獨立進行50 次蒙特卡羅仿真，歸納了傳統當前統計模型算法與本文提出的當前統計模型加速度方差自適應方法跟蹤目標的跟蹤誤差情況。表1中顯示本文方法明顯優于傳統算法，從統計意義上說明改進方法效果好。

圖2 加速度方差變化的跟蹤效果圖(200～250 s）

表1 多機動情況目標跟蹤算法性能比較(變量的RMSE 值）

從仿真結果看，當目標作勻速運動或小加速運動時，加速度方差自適應與固定跟蹤算法的跟蹤精度都比較好;但當目標以較大的加速度進行機動時，加速度方差自適應算法的收斂速度和跟蹤精度要明顯優于加速度方差固定算法。此時的跟蹤誤差也明顯要比自適應算法大，且其波動幅度也較大。可見，加速度自適應跟蹤算法優于方差固定跟蹤算法。

3.2 機動頻率α 自適應跟蹤算法仿真

設機動目標沿x 軸運動狀態和航跡同4.1節。采樣時間T=1 s，α 取0.001;amax=8*g，amin=－8*g;參數μ=0.000005。兩段代表性仿真結果如下:

圖3所示為150～180 s時間段目標以較大的加速度作大機動時的仿真結果。圖4所示為200～250 s時間段內目標既有較小的加速運動也有勻速運動狀況下的仿真結果。

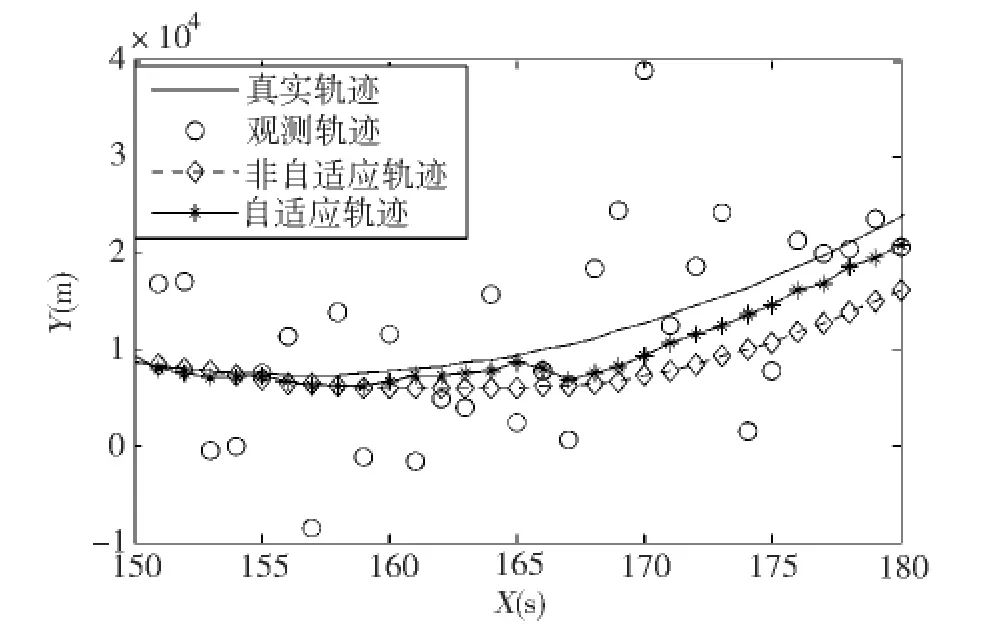
圖3 機動頻率變化的跟蹤效果圖(150～180 s）

由仿真結果圖可見，當目標勻速或加速度較小時，機動頻率α 自適應跟蹤算法與機動頻率α 固定跟蹤算法的跟蹤效果都比較好，但是當目標以較大的加速度進行機動時，機動頻率自適應算法的收斂速度和跟蹤精度要優于機動頻率α 固定跟蹤算法。

圖4 機動頻率變化的跟蹤效果圖(200～250 s）

表2為機動目標在各種變加速度情況下觀測噪聲隨機生成。同樣，每種情況獨立進行50 次蒙特卡羅仿真，歸納了傳統當前統計模型算法與本文提出的當前統計模型機動頻率α 自適應調整方法跟蹤目標的跟蹤誤差情況。表2中也顯示本文方法優于傳統算法，從統計意義上說明改進方法效果明顯。

表2 變加速度機動情況目標跟蹤算法性能比較(變量的均方根誤差RMSE 值）

綜合以上仿真結果，當目標作勻速運動或小加速運動時，兩種改進算法與傳統固定參數跟蹤算法的跟蹤精度相當;但時，當目標以較大的加速度機動時，加速度方差自適應算法和機動頻率α 自適應算法的收斂速度和跟蹤精度都明顯優于參數固定跟蹤算法，且加速度方差自適應跟蹤算法要優于機動頻率自適應跟蹤算法。

4 結束語

文中分析了當前統計模型跟蹤機動目標存在的不足，仿真驗證了采用加速度方差σ2a自適應跟蹤算法和機動頻率α 自適應改變跟蹤算法的跟蹤效果，提出了兩種方式的自適應參數的變化方法，分別就不同情況進行仿真分析跟蹤性能。仿真效果驗證了文中的兩種改進方法在機動目標跟蹤時的良好效果。

［1］潘平俊，馮新喜，趙曉明.機動目標模型研究與發展綜述［J］.指揮控制與仿真，2006，28(3）:12-15.

［2］胡洪濤，敬忠良，田宏偉，等.基于當前統計模型的模糊自適應跟蹤算法［J］.系統仿真學報，2005，17(2）:293-299.

［3］李彬彬，王朝英.一種基于當前統計模型的改進目標跟蹤算法［J］.彈箭與制導學報，2008，28(2）:81-83.

［4］王軍政，沈偉，趙江波.機動目標跟蹤中機動頻率的自適應調整［J］.北京理工大學學報，2007，27(1）:38-41.

［5］沈福民.自適應信號處理［M］.西安:西安電子科技大學出版社，2008.