一種新的保險投資組合優化模型
張月,曲坤,王麗媛
(1.大連理工大學 應用數學系,遼寧 大連116024;2.大連交通大學 理學院,遼寧 大連 116028)
0 引言
在保險市場中,保險公司通常把所有的風險項目看做一個整體,根據不同的風險項目在整個投資組合中所占的比例對被保險人收取合理的保費,根據收取保費的大小以達到安全運營的目的.然而在保險和金融市場中,風險無處不在,保費的制定自然離不開對風險的合理度量,風險表示損失的不確定性及其發生的概率.目前關于風險度量的方法有很多種,如:方差原理[1]、破產概率[1]、VAR 方法[2]、一致性風險度量方法[3]等.不同的度量方法取決于對風險的不同認識,結果往往也不同.常見的方差原理[1]中,方差依賴于隨機變量取值的大小,它表示收益的各種可能值與期望收益的偏離程度,因此只能計算出關于損失變量的二階矩,并且方差作為不確定性的度量只適用于損失分布是正態分布(即對稱分布)的情況,對于其他的偏斜分布(尖峰、厚尾等),方差無法正確反映出風險的大小,因此在實際應用中這種度量方法存在著不足.而熵代表不確定性程度的度量,它根據隨機變量可能取到的概率進行計算,不依賴于隨機變量本身取值的大小,它表示的是概率密度偏離均勻分布的程度,是把風險系統看做一個整體進行度量.在保險研究中,人們最關心的是極端事件發生時風險的大小,即文獻[1]中所講的破產概率,這時損失的概率分布是非對稱的,僅用方差來度量的風險大小顯然不夠,還應包括損失的高階矩信息,而熵代表高階矩,因此可以用熵作為方差度量風險的一個有效補償.文獻[1]通過將破產概率中的安全系數轉化為方差,用方差度量風險.基于以上對方差和熵的對比分析,本文用熵來作為方差度量保險投資組合中風險的補充,提出一種度量風險的新模型:均值-方差-熵模型,以便使風險的度量更加有效.
1 預備知識
在信息論中,熵代表無知程度的度量,它的值越大,意味著我們對所解決的問題知道的信息越少.金融和保險市場的信息是不完全的,也就是存在一定的不確定性即風險,隨著不確定性的減小也就是熵的減小,我們才能更加有效地將風險控制住,本文基于熵作為風險的度量,以文獻[1]中的聚合風險模型為基本假設,將保險投資組合中各風險項目所占的比例(即損失變量的概率分布)轉變成對風險項目所收取的保費的表達式,得到了關于保費的優化模型,在給出具體的優化模型之前,我們先來介紹一下該模型的理論依據:
1.1 最大熵原理及其數學表達[4]
所謂的最大熵原理就是在根據部分信息進行推理時,我們應使用的概率分布,必須是在服從所有已知觀測數據的前提下使熵函數取最大值的那個概率分布.熵最大,表明我們除了具有統計矩的信息外,對待求的概率分布一無所知.這是我們能做出的僅有的無偏分配,因此最大熵原理可表達為下述數學規劃問題:
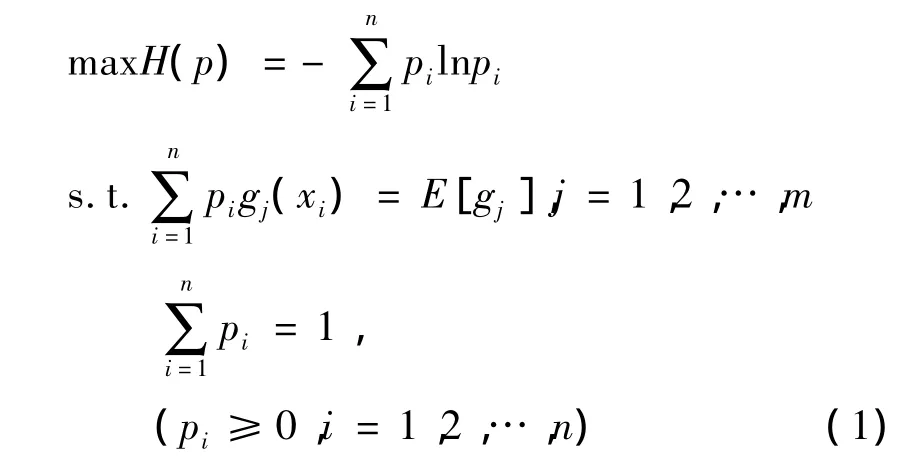
其中,p=(p1,p2,…,pn)為待估的概率分布,gj(j=1,2,…,m)表示各階統計矩函數,E(·)是由實驗觀測得到的各階統計矩的期望值.
1.2 聚合風險模型基本假設[1]
2 均值-方差-熵優化模型
保險業的存在是由于人們愿意支付高于他們的期望索賠額的保費以尋求保險保障,而保險公司的收益等于他們收取的保費減去其索賠額(其中不考慮其他運營成本).因此如何定價一個合理的保費才是保險公司決定一個有效的保險投資組合的關鍵.
假設保險市場有k個不同的風險項目ψ1,ψ2,…,ψk,每個風險項目 ψj包含 Nj種不同風險索賠Sj,其中Sj服從泊松參數為λj的復合泊松分布.對于ψj中的任一風險,保費為xj=λjE[X]+lj,其中xj代表保費;lj代表風險負載.
假設風險項目ψj在保險投資組合中所占的比例為nj,其大小取決于所收取的保費 xj,且,因此保險投資組合的收益為:
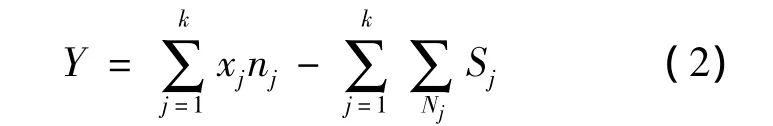
為保費 x=(x1,x2,…,xk)的函數.
式(2)的矩母函數為[1]
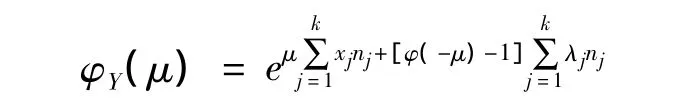
則累積矩母函數為
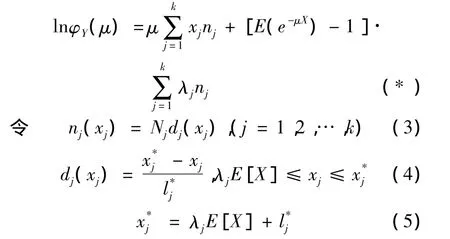
因此均值-方差-熵優化模型為:
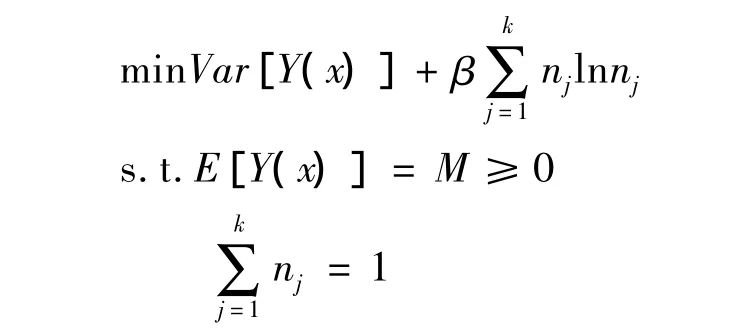
由式(*)可得保險投資組合的期望收益和方差分別為累積矩母函數的一、二階矩在μ=0處的值,即
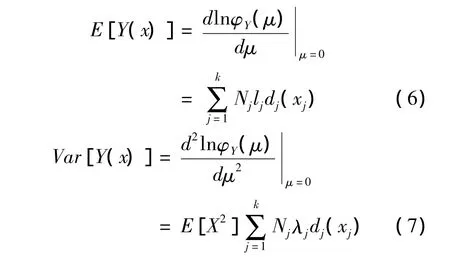
由于E[X2]的大小與優化問題并沒有太大的關系,因此為方便起見令E[X2]=1.
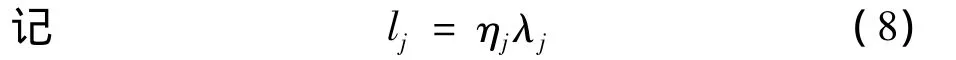
ηj代表風險厭惡指數.
將(4),(5),(7)代入(3)得
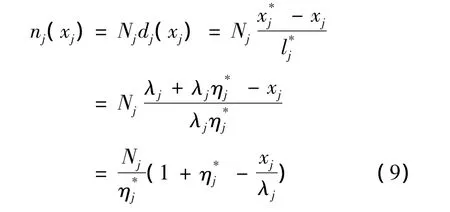

將式(9),(10),(11)代入上面優化模型整理得:
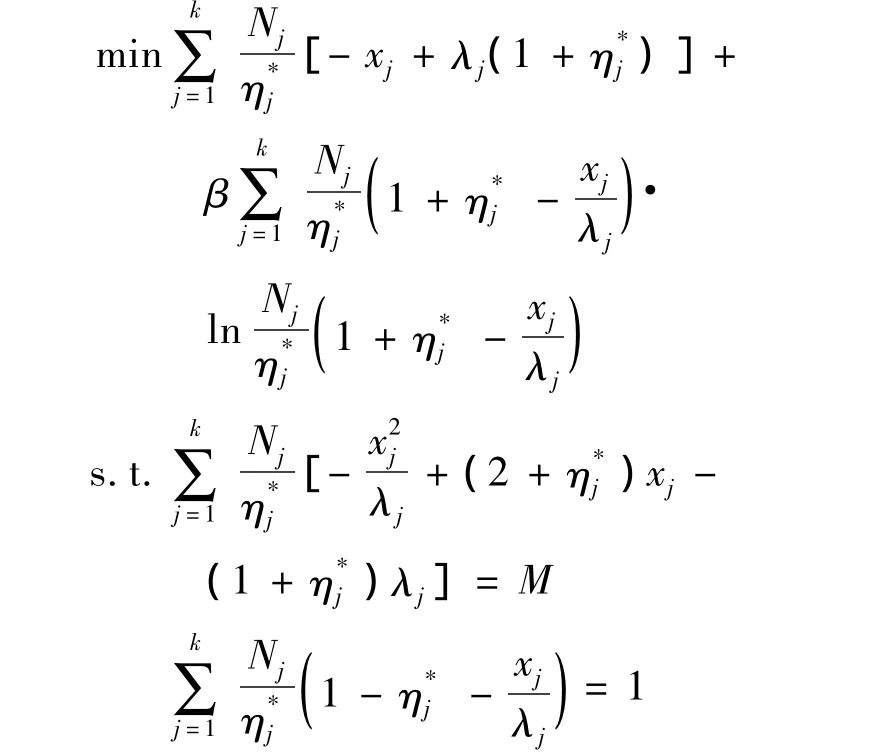
可見該模型將投資比例nj轉化為了關于保費xj的表達式,它不同于一般的均值-方差優化模型,其約束條件是關于保費xj的二次函數,其中包含一次項并且不包含混合項,通過調節加權系數β的大小可以求解該凸規劃問題.該問題為凸規劃問題,一定有唯一最優解,即我們可以計算出保費xj.當β很小時,求得的保費xj結果主要是方差起作用而熵函數不起作用,而隨著β的增加,熵函數起的作用逐漸增加,這樣求得的保費xj主要是熵函數在起作用.
3 結論
通過分析保險投資組合中風險的不確定性的本質,以文獻[1]中的聚合風險模型為基礎,論述了熵可以作為風險度量的一種方法,得到了關于保費的保險投資組合優化模型.與文獻[1]中的方差模型相比,該模型從風險作為一個整體系統及風險距離期望的波動情況兩個方面一起來反映風險,是一個比較合理的風險度量模型.
[1]FRANCO MORICONI.A pricing model in a sensitive insurance market[J].Astin Bulletin,1980(11):52-60.
[2]JORION P.Measure the risk in value at risk[J].Financial Analysts Journal,1996(11):47-55.
[3]ARTZNER P.Coherent measure of risk[J].Mathematical finance,1999(9):203-228.
[4]JAYNES E T.Information theory and statistical mechanics[J].The Physical Review,1957(106):620-630.
[5]李華.均值-叉熵證劵投資組合優化模型[J].數學的實踐與認識,2005(5):65-70.
[6]葉中行.數理金融[M].北京:北京:科學出版社,2002.

