應用模糊控制方法的擾動引力計算

王激揚

海軍某軍事代表局，北京 100854

應用模糊控制方法的擾動引力計算

王激揚

海軍某軍事代表局，北京 100854

為了解決彈道導彈擾動引力計算精度與速度的矛盾，利用模糊控制的特點，通過對模糊控制器的改進，成功將模糊控制運用于擾動引力的計算。從計算思路、基本點擾動引力的計算、分級模糊控制規則的具體改進等方面進行了詳細分析，仿真結果表明:運用所提出的模糊控制方法計算得到的擾動引力與真值誤差很小，而計算速度遠快于分層點質量法等常規方法。

擾動引力;分級模糊控制;誤差;改進

由于地球質量分布的復雜性，導致了地球引力場的復雜性，使它不同于正常引力場。在地球外部空間的任意點，實際引力加速度不同于正常引力加速度，因而實際重力也不同于正常重力，稱實際引力場與正常引力場的差為地球擾動引力場;實際引力加速度與正常引力加速度之差為擾動引力加速度，簡稱擾動引力［1］。

擾動引力在彈道導彈飛行過程中帶來的落點偏差是不可忽略的，因此必須準確的計算導彈飛行彈道上的引力加速度，它不僅是彈道導彈彈道計算的基礎，也是彈道導彈制導或導航需要解決的問題。

現有的擾動引力賦值方法，有點質量方法、球諧函數方法等。對大量的彈道計算尤其是由彈載計算機實時計算擾動引力，質點法仍遠未解決快速計算問題。原因在于采用該方法時，空間任一點的擾動引力都需通過數千個乃至上萬個擾動質點引力的求和來得到。而模糊控制的最大特點就是不需要對所要控制的過程(或系統)進行數學描述，而是直接根據過程的輸入條件——測量值與設定值的偏差及其偏差變化率，便能得到最優的控制輸出值［2］。因此，根據擾動引力只是空間位置的函數這一特點，結合模擬控制，提出擾動引力快速計算的一種新方法。

經典模糊控制器的設計通常以被控變量相對于給定值的偏差和偏差變化率作為控制輸入，控制規則如下:if(偏差=E，偏差變化率=EC)then(控制量=U)，顯然這是單變量PD調節器，控制變量限于單變量系統［2］。然而，空間位置包括經度、緯度及高程3個因素，直接運用上述模糊控制方法會遇到很多問題，因此有必要對經典模糊控制器加以改進，以適用擾動引力的計算問題。

1 基本思路

模糊控制方法運用的關鍵在于模糊控制器必須與所要解決的問題相匹配，因而，我們首先對模糊控制器進行設計，然后計算擾動引力的初始數據點集，進而根據所求位置計算偏差和偏差變化率，再根據模糊控制規則進行結果計算和初始數據點集的修正，如圖1所示。

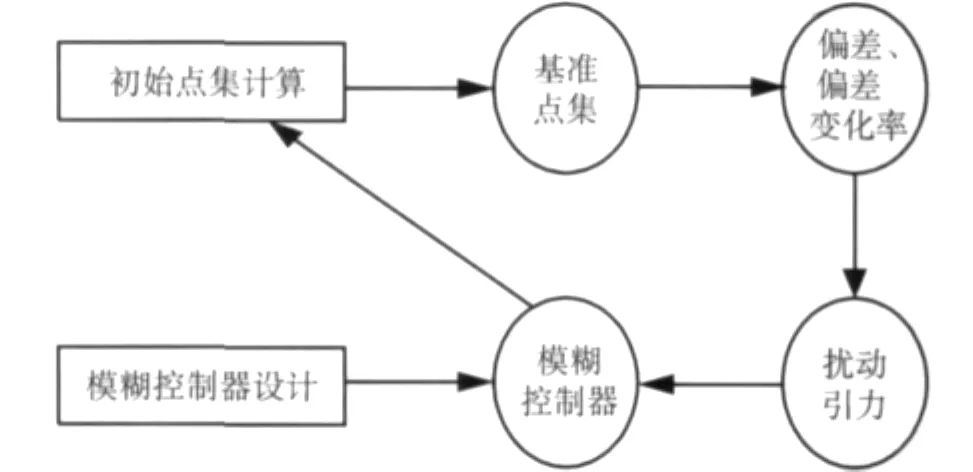
圖1 擾動引力模糊計算的基本思路框圖

下面將結合以上計算思路進行探討和分析。

2 初始點集擾動引力的計算

真實引力位與正常引力位的差別稱為擾動引力位，即

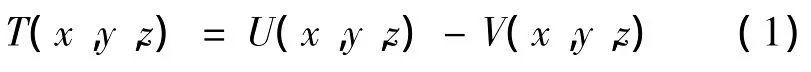
T表示擾動引力位，U代表真實引力位，V為正常引力位。擾動引力為對位置的梯度即為擾動引力，即

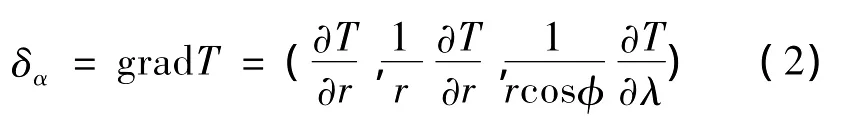
其中，r為地心距;φ為地心緯度;λ為地心經度。

對擾動引力 δα(α = γ，λ，φ)，當將(γ，λ，φ)轉換成局部坐標(ξ，η，ζ)后，δα(α = γ，λ，φ)可表示成(ξ，η，ζ)的函數。

空域劃分采用一般有限元方法，即將Ωe考慮成8節點六面體，r=8取結點為Ωe的8個頂點Ai，每個結點再分別延γ，λ，φ方向向外把相鄰單元的一個結點包括進來，構成s=32的延拓域Ω'e［3］。

在單元Ωe內，我們采用階次為m的多項式來逼近 δα，(α =γ，λ，φ)，m的大小視計算速度與精度而定。取m=20，n=8(n為節點數)。取三元多項式類為

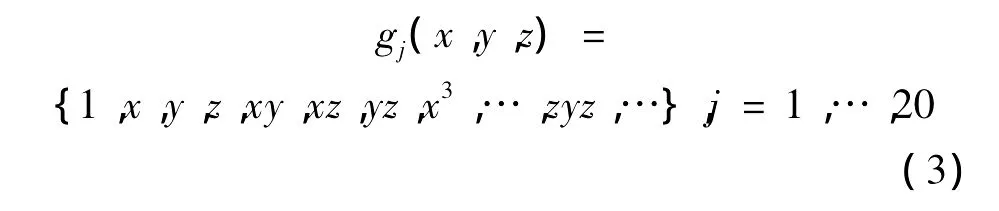
則逼近函數為20次多項式

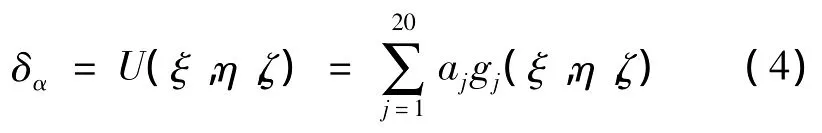
待定系數aj可由下式確定:

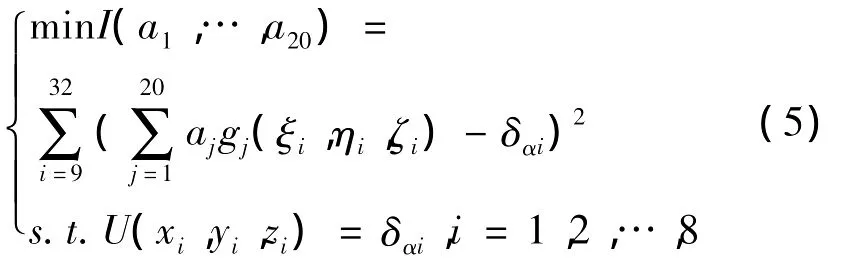
3 模糊控制器的設計

如圖1所示，初始點集的擾動引力計算完成后，基準點集也就確定了，偏差和偏差變化率的計算相對簡單，接下來的關鍵問題就是模糊控制器的設計，下面就這方面進行詳細分析。

3.1 設計思路

文獻［4］提出了一種分層多規則集結構，它將多變量模糊控制器分解為一個有層次的多個簡單規則集組成的結構。在此基礎之上，根據高程、經度和緯度分別對擾動引力的影響大小不同，對文獻［4］中提出的分層多規則集結構進行改進，將對系統性能(高程)影響最大的因素選做一級變量，其次為二級變量(緯度)，依此類推。其規則如下:

1 級規則——if(X11isA11andX21isA12…andXn1isA1n)，then(Y1isB1)。

k級規則——if(X1kisAk1andX2kisAk2…andXnkisAkn)，then(YkisBk)。

Akn為第nk個輸入Xnk的模糊變量值，Bk為第k個輸出Yk的模糊變量值。

上述結構中，第一級給出近似的輸出值y1，此后，y1通過第二層規則修正為y2，依此類推。顯然，各級規則不但包含本機輸入變量，而且前一級的輸出變量也作為本級別輸入變量，兼顧了各級別間變量的相互關系。

3.2 模糊控制規則

根據上節中設計的模糊控制器，將模糊規則庫中的“if――then”規則轉換成擾動引力與初始擾動引力點集的某種映像，然后結合彈道計算流程進行諸元解算。

空間位置(γ，λ，φ)中，顯然，對擾動引力的影響最大的是地心距r，其次是緯度φ，然后是經度λ。因此，根據3.1節中設計的模糊控制規則選定地心距r為1級變量，緯度φ為2級變量，經度λ為3級變量，模糊規則結構如圖2所示。

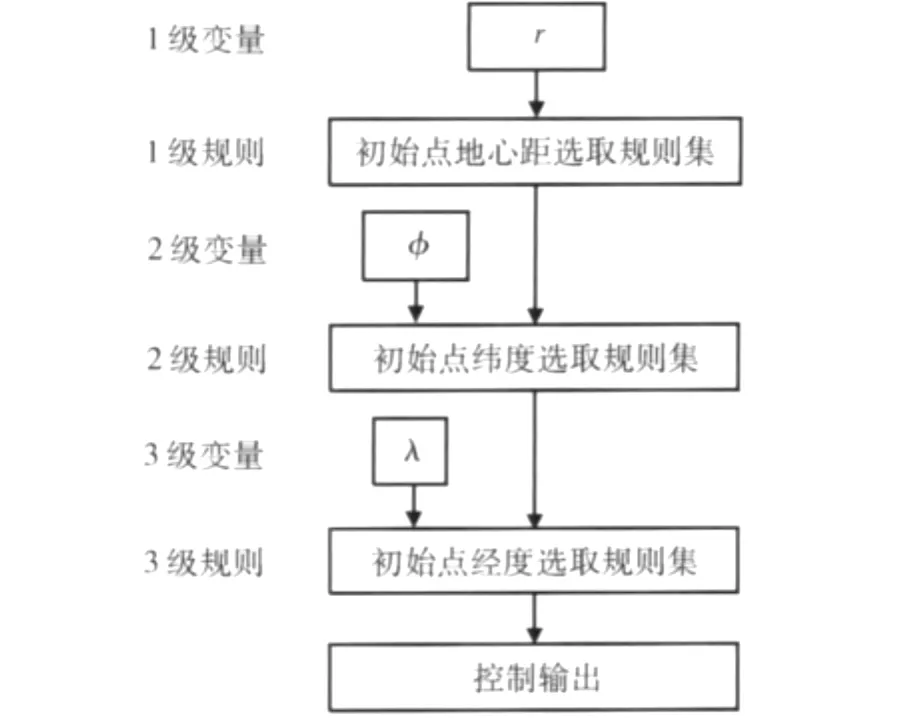
圖2 擾動引力計算的3級模糊規則圖

如圖2所示，在每一級中，上一級的輸出就當成了一個常數輸入量，多變量模糊控制器分解成了一個有層次的多個簡單規則集合組成的結構。針對每個簡單規則，利用經典模糊控制器來解決。

變量(γ，λ，φ)的域分為若干個區間，每個區間相應于一個模糊子集X-(x1，x2，…，xn)，各分點為特征點，其隸屬函數曲線［5］如圖3所示。

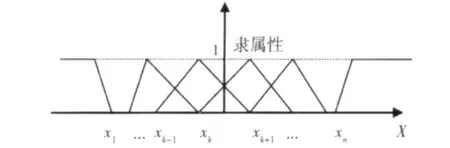
圖3 隸屬函數曲線圖

設輸出變量的域為Z，詞集取為C1，C2，…Cm，在輸出變量的域上分別取m個點為輸出特征點(c1，c2，…cm)，并定義輸出變量詞集中的各模糊子集都是單點模糊集，即隸屬函數為:

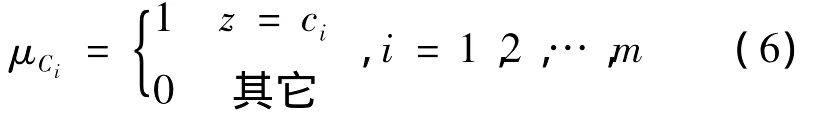
輸入輸出變量模糊子集定義中的特征點數(即模糊子集的個數)，以及各特征點取值需要根據經驗數據來選取，而且對于不同的彈道這些參數是不同的，只有在經過初步計算的基礎上才能選擇出收斂速度較快的參數值。另外，對于輸入輸出變量模糊子集的個數選取來說，應根據具體的精度要求和分不同的量級區間來定，如果參數選擇不當，則有可能在零點附近引起振蕩。所以對于需要收斂速度較快并且精度較高的地方，需要選擇較多的模糊子區間，而在落點偏差較大的區域內，可以較粗的選擇模糊子區間［5］。

4 算例

計算采用的原始數據是某區域的點質量數據。根據這些數據選取初始點集，作為逼近所用的數據基礎(即已知函數值)，初始原則如下:主動段的高度為200km，發射區域取為以發射點為中心±10經緯度的方形區域，取相鄰節點間的高度差為10km，相同高度層面上相鄰節點間的緯度和經度差為10°。空間點擾動引力的標準值根據第2節中的方法計算得到，經過計算可知:采用這種方法計算的標準值與點質量法計算精度相當，但計算速度更快。計算結果如圖4所示。采用不同方法計算結果如表1所示。

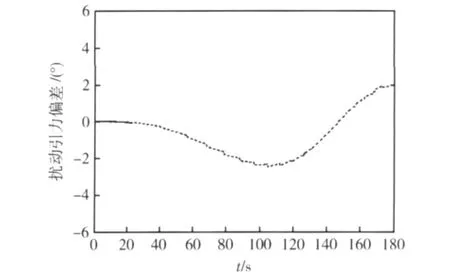
圖4 彈道導彈擾動引力模糊控制方法計算誤差

表1 不同方法計算擾動引力比較

由圖可知，所使用的模糊控制方法用于擾動引力的計算，其結果與分層點質量方法計算得到的結果相差很小，具有很高的精度。經過比較，其計算時間約為分層點質量方法的1/50，而且經過模糊控制規則的不斷改進，其計算時間會更短。

5 結束語

擾動引力快速計算問題直接關系到諸元裝訂的時間，對彈上計算機的性能也起到了一定的制約。分級多規則模糊控制結構的使用有效解決了在現階段無法獲得控制位置與擾動引力間精確數學模型情況下，多變量輸入多變量輸出的模糊控制問題。仿真計算結果表明，運用所提出的模糊控制方法計算得到的擾動引力與真值誤差很小，而計算速度遠快于分層點質量法和第3節中提出的方法;另一方面，經驗和專家知識也是分級模糊控制簡單規則制定的關鍵，其規則的改進有待進一步自我調整和改進。

［1］王昱.擾動引力的快速計算及其對降落落點偏差的影響［D］.國防科技大學，2002.(WANG Yu.The method of rapid calculation gravitational perturbations and the effect to the fall point deviation.Master’s thesis.National Defense University.2002.)

［2］張蕊，葉建華.多變量模糊控制工程應用方法［J］.上海電力學院學報，2008，(3):223-224.(ZHANG Rui，YE Jianhua.The Method of Multivariable Fuzzy Control Engineering Applications.Shanghai Institute of Electric Power Journal，2008，(3):223-224.)

［3］趙東明，吳曉平.利用有限元方法逼近飛行器軌道主動段擾動引力［J］，宇航學報，2003，24(3):309-313.(ZHAO Dongming，WU Xiaoping，Approaching Vehicle Using Finite Element Methods Section of the Track active Gravitational Perturbations［J］，Astronautics Journal.2003，24(3):309-313.)

［4］戴忠達，張曾科，湯儉.一種改進的模糊控制器及其應用［J］.自動化學報，1990，16(3):258-261.(DAI Zhongda，Zhang Zengke，Tang Jian.An Improved Fuzzy Controller and its Application ［J］.Automation Journal 1990，16(3):258-261.)

［5］潘剛.遠程彈道導彈快速諸元計算方法研究［D］.國防科技大學研究生院，2002.(PAN Gang.Rapid Calculation Long-range Ballistic Missiles of Various Element Method［D］.National Defense University Graduate Master’s Degree Thesis.2002.)

［6］賈沛然，陳克俊，何力.遠程火箭彈道學［M］.長沙:國防科技大學出版社，1993.(JIA Peiran，CHEN Kejun，HE Li.Long Range Rocket Ballistics［M］.Changsha:National Defense University Press.1993.)

The Application of Fuzzy Control Method to the Disturbing Gravitation Calculation

WANG Jiyang
The Representive Department of The Navy，Beijing 100854，China

In order to solve the contradictions of precision and speed of gravity disturbance calculation，the characteristics of fuzzy control are used．Based on the improved fuzzy controller，the fuzzy control method is successfully used in the disturbing gravitation calculation．The computing ideas，basis points computation，hierarchical fuzzy control rules of specific improvement are analyzed in detail．The calculation example shows that the results biases are small by using the method of fuzzy control and the computing speed is faster than the speed obtained with conventional methods such as the stratified point quality method．

Disturbing gravitation;Hierarchical fuzzy control;Bias;Improvement

TP273+.4

A

1006-3242(2012)01-0020-03

2011-08-31

王激揚(1968-)，男，江蘇武進人，博士，高級工程師，主要研究方向為飛行器控制、制導與仿真。