基于匹配追蹤算法的復(fù)合材料沖擊損傷成像技術(shù)*
馮勇明,周 麗
(南京航空航天大學(xué)機(jī)械結(jié)構(gòu)力學(xué)及控制國(guó)家重點(diǎn)實(shí)驗(yàn)室,江蘇 南京 210016)
先進(jìn)的復(fù)合材料已在航空航天飛行器結(jié)構(gòu)上得到了廣泛應(yīng)用,但復(fù)合材料結(jié)構(gòu)在制造和使用過(guò)程中,不可避免地會(huì)受到損傷,尤其是低能量物體的沖擊造成的損傷,這種損傷往往表現(xiàn)為目不可檢的內(nèi)部分層、基體開(kāi)裂和纖維斷裂,對(duì)結(jié)構(gòu)的安全使用造成嚴(yán)重威脅。因此,及時(shí)準(zhǔn)確檢測(cè)并識(shí)別出復(fù)合材料結(jié)構(gòu)內(nèi)部損傷、確定損傷程度并進(jìn)行連續(xù)監(jiān)測(cè)是當(dāng)前關(guān)注的焦點(diǎn)。目前,在復(fù)合材料結(jié)構(gòu)的健康監(jiān)測(cè)領(lǐng)域,Lamb波能在結(jié)構(gòu)中傳播較長(zhǎng)的距離,被認(rèn)為是較有前景的一種局部損傷檢測(cè)方法[1-2],非常適合監(jiān)測(cè)機(jī)翼和機(jī)身這樣的大面積結(jié)構(gòu)[3-4]。在結(jié)構(gòu)中布置一定的傳感器,主動(dòng)激勵(lì)Lamb波信號(hào),通過(guò)對(duì)接收的損傷前和損傷后的Lamb波信號(hào)進(jìn)行一定的處理,就可以提取應(yīng)力波包含的與損傷有關(guān)的特征信息,從而進(jìn)行損傷定位及損傷大小的判斷[5]。
T.R.Hay等[6]對(duì)蜂窩夾層結(jié)構(gòu)中應(yīng)力波的傳播特性進(jìn)行了研究,為基于應(yīng)力波的損傷監(jiān)測(cè)方法在復(fù)合材料結(jié)構(gòu)中的應(yīng)用提供了指導(dǎo)。M.M.Howard等[7]驗(yàn)證了壓電傳感器環(huán)方法監(jiān)測(cè)復(fù)合材料結(jié)構(gòu)的可行性;A.Swartz等[8]分別采用小波衰減法、功率譜的相關(guān)系數(shù)法等監(jiān)測(cè)方法對(duì)結(jié)構(gòu)中的損傷進(jìn)行了監(jiān)測(cè)。近年來(lái),許多學(xué)者[9-11]采用短時(shí)傅里葉變換(STFT)、小波變換(WT)、希爾伯特-黃變換(HHT)等時(shí)頻分析方法對(duì)監(jiān)測(cè)信號(hào)進(jìn)行分析,并取得了一系列成果,但這些方法的時(shí)頻分辨率都不理想,并且未考慮彌散效應(yīng)對(duì)信號(hào)的影響。J.C.Hong等[12]將匹配追蹤方法運(yùn)用于應(yīng)力波信號(hào)的處理中,但他們假設(shè)應(yīng)力波信號(hào)是單模態(tài)的、非彌散的,并未精確建立彌散效應(yīng)與原子的調(diào)頻斜率之間的關(guān)系,計(jì)算結(jié)果精度不高。
本文中,使用Chirplet原子匹配彌散的窄帶脈沖信號(hào),并采用自適應(yīng)信號(hào)處理方法——匹配追蹤方法對(duì)監(jiān)測(cè)信號(hào)進(jìn)行分解,對(duì)Lamb波信號(hào)進(jìn)行時(shí)頻分析,證明Chirplet原子能準(zhǔn)確匹配失真變形的窄帶脈沖信號(hào)。利用對(duì)碳纖維復(fù)合材料板的沖擊損傷進(jìn)行實(shí)驗(yàn)檢測(cè),采用匹配追蹤方法對(duì)包含有損傷信息的應(yīng)力波信號(hào)進(jìn)行時(shí)頻處理,提取損傷特征值,并采用損傷概率成像方法定位結(jié)構(gòu)中的沖擊損傷。
1 匹配追蹤方法
匹配追蹤(matching pursuits,MP)方法是S.G.Mallat等[13]在1993年提出的一種自適應(yīng)信號(hào)處理方法,該方法將待分析信號(hào)重復(fù)迭代投影到龐大的波形字典庫(kù)中,并從字典庫(kù)中選擇最適合匹配某段待分析信號(hào)的波形。MP方法克服了STFT變換中窗函數(shù)固定,以及小波變換中窗函數(shù)的頻率參數(shù)與尺度參數(shù)成反比的缺點(diǎn),使用能匹配信號(hào)時(shí)頻特性的波形來(lái)靈活地表示信號(hào)。MP方法的核心問(wèn)題是構(gòu)建龐大的冗余字典庫(kù),并從中快速檢索出最佳的匹配原子,字典庫(kù)檢索的計(jì)算速度問(wèn)題顯得尤為重要。
設(shè)D={gr}r∈Γ是由P>N個(gè)范數(shù)為1的向量所形成的字典庫(kù)。該字典庫(kù)中包含N個(gè)線性無(wú)關(guān)的向量,這N個(gè)向量構(gòu)成長(zhǎng)度為N的信號(hào)空間CN的一組基。匹配追蹤算法首先將信號(hào)f投影到一個(gè)向量gr0∈D上,并計(jì)算出余項(xiàng)Rf,

由于Rf與gr0正交,因此

為了極小化 ‖Rf‖,取gr0∈D,使得 〈f,gr0〉為極大值。在某些情況下為使計(jì)算更為有效,只需找到向量gr0使之幾乎為最優(yōu)

式中:α∈(0,]1為最佳因子。匹配追蹤方法通過(guò)反復(fù)地迭代對(duì)余項(xiàng)作進(jìn)一步分解。記R0f=f,對(duì)m≥0,設(shè)第m個(gè)余項(xiàng)Rmf已經(jīng)計(jì)算出來(lái),那么下一步迭代是選取gr0∈D,使得

將Rmf投影到grm上,得到

由Rm+1f與grm的正交性,得到

即整個(gè)分解過(guò)程是滿足能量守恒定律的。對(duì)m從0到M-1求和,得

當(dāng)m→∞時(shí),‖Rmf‖按指數(shù)級(jí)收斂于0。迭代過(guò)程可以通過(guò)指定迭代次數(shù)或控制信號(hào)殘值完成。
根據(jù)實(shí)際應(yīng)用可以選擇特殊的字典D。在結(jié)構(gòu)健康監(jiān)測(cè)中,主要應(yīng)用時(shí)頻原子字典,如Gabor原子、Chirplet原子等。在進(jìn)行具體的標(biāo)準(zhǔn)匹配追蹤算法時(shí),連續(xù)的參數(shù)空間必須適當(dāng)?shù)仉x散化。本文中,匹配追蹤方法選用由Chirplet原子組成的字典庫(kù)
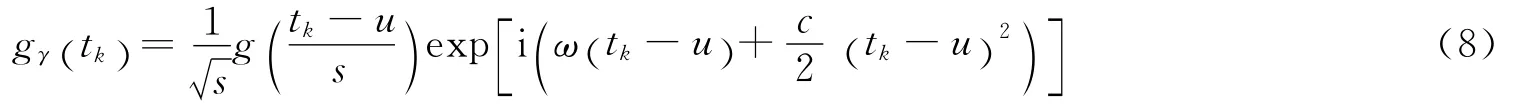
式中:tk表示時(shí)間離散點(diǎn),g(tk)=;索引γ=(s,u,ω,c),其中s為尺度,u為時(shí)間中心,ω0為角頻率中心,c為調(diào)頻斜率。該原子的角頻率ω(tk) 隨時(shí)間變化,ω(tk)=ω+c(tk-u)。Chirplet原子以及WVD分布如圖1所示。
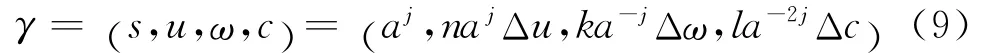
式中:j、n、k、l為整數(shù)。
研究中模擬與實(shí)驗(yàn)測(cè)得信號(hào)均為實(shí)數(shù)信號(hào),應(yīng)用MP算法時(shí)需要使用實(shí)數(shù)原子
Chirplet原子組成的字典庫(kù)是Gabor原子組成字典庫(kù)的延伸,當(dāng)Chirplet原子中的變量c=0時(shí),Chirplet原子即為Gabor原子。Chirplet原子字典庫(kù)的索引離散化后為

圖1 Chirplet原子及其WVD分布Fig.1The Chirplet atom and its WVD

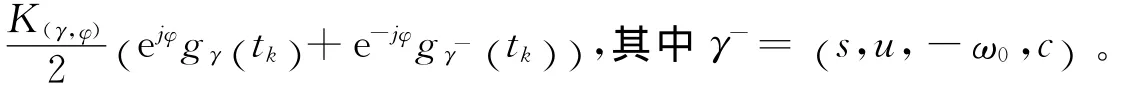
2 數(shù)值模擬驗(yàn)證
為驗(yàn)證本文中提出的MP方法的有效性,建立帶損傷鋁板的二維有限元模型。模型如圖2所示,尺寸為80cm×0.1cm,在距離壓電片12和21.5cm處布置缺口用來(lái)模擬損傷,缺口尺寸為0.025cm×0.05cm。在模擬時(shí)采用2對(duì)剪切力模擬激勵(lì)源產(chǎn)生應(yīng)力波。激勵(lì)信號(hào)采用窄帶波信號(hào)

式中:尺度s為量綱一因數(shù),s=6×10-6,激勵(lì)頻率f0=250kHz。
MP方法對(duì)模擬結(jié)果進(jìn)行分解重構(gòu)后的信號(hào)如圖3(a)中虛線所示,重構(gòu)信號(hào)與模擬幾乎重合,表明Chirplet原子能很好地匹配彌散脈沖。MP方法得到的時(shí)頻能量分布如圖3(b)所示,能得到信號(hào)的時(shí)頻能量分布圖,并能分辨中間2個(gè)重疊的反射信號(hào)。圖3(c)是信號(hào)的小波尺度譜,它不能分辨重疊在一起的反射信號(hào)。
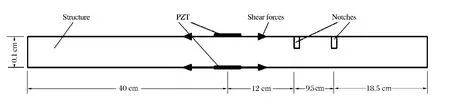
圖2 數(shù)值模擬模型Fig.2The model of numerical simulation

圖3 模擬結(jié)果分析Fig.3The results of numerical simulation
3 損傷概率成像方法
3.1 基于信號(hào)能量譜的損傷指標(biāo)
在結(jié)構(gòu)運(yùn)行之前的完好狀態(tài)下測(cè)得Lamb波信號(hào),稱為基準(zhǔn)信號(hào);然后在結(jié)構(gòu)運(yùn)行之后,再次測(cè)得Lamb波在結(jié)構(gòu)中的傳播信號(hào),稱為監(jiān)測(cè)信號(hào);將監(jiān)測(cè)信號(hào)與基準(zhǔn)信號(hào)進(jìn)行比較以判斷結(jié)構(gòu)中是否存在損傷,并進(jìn)一步確定損傷的位置、程度等信息。監(jiān)測(cè)信號(hào)與基準(zhǔn)信號(hào)之間的差異系數(shù),稱為損傷指標(biāo)(DI),本文中通過(guò)提取結(jié)構(gòu)損傷前后Lamb波信號(hào)能量特征的差異系數(shù)即DI來(lái)確定損傷指標(biāo)。選用Chirplet原子對(duì)基準(zhǔn)信號(hào)和監(jiān)測(cè)信號(hào)分別進(jìn)行MP變換,提取信號(hào)主要頻帶的局部時(shí)間-能量密度,定義損傷指標(biāo)如下
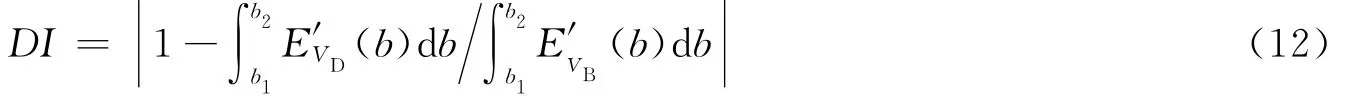
式中:VB是結(jié)構(gòu)完好狀態(tài)下測(cè)得的Lamb波基準(zhǔn)信號(hào),VD是結(jié)構(gòu)損傷后測(cè)得的Lamb波監(jiān)測(cè)信號(hào),E′(b)是信號(hào)經(jīng)過(guò) MP分析后在尺度 [a1,a2]、時(shí)刻b下的局部時(shí)間 -能量密度,[b1,b2]表示對(duì)信號(hào)進(jìn)行MP分析的時(shí)間范圍。
理想情況下,如果結(jié)構(gòu)中不存在損傷,那么VB和VD完全相同,DI=0。但在實(shí)際情況中,由于外界環(huán)境如溫度、濕度、噪聲等影響,即使在無(wú)損狀態(tài)下測(cè)得的監(jiān)測(cè)信號(hào)也會(huì)與基準(zhǔn)信號(hào)有不小的差別,難以區(qū)分這一差異是由結(jié)構(gòu)損傷引起的還是因環(huán)境變化造成的。為克服這一缺陷,本文中用概率統(tǒng)計(jì)方法,對(duì)式(12)表示的損傷指標(biāo)進(jìn)行重新定義。
首先在結(jié)構(gòu)完好狀態(tài)下測(cè)得M組Lamb波信號(hào)VBi,將其中一組信號(hào)(如第1組,i=1)作為基準(zhǔn)信號(hào)。其余M-1組信號(hào)相對(duì)于基準(zhǔn)信號(hào)的損傷指標(biāo)定義為
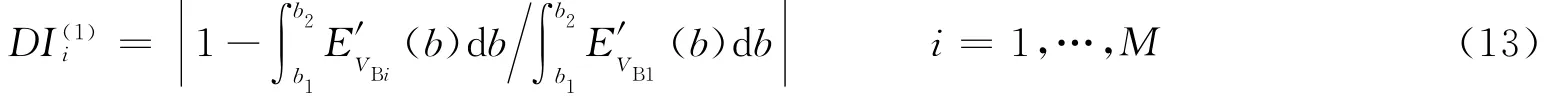
同樣地,在結(jié)構(gòu)有損狀態(tài)下測(cè)得N組Lamb波信號(hào)VDj,這N組信號(hào)相對(duì)基準(zhǔn)信號(hào)的損傷指標(biāo)定義為
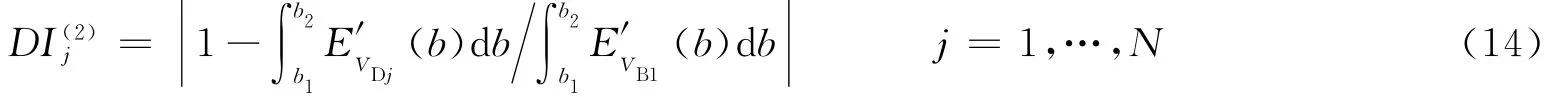
本文中采用概率統(tǒng)計(jì)函數(shù)t來(lái)對(duì)上述損傷指標(biāo)進(jìn)行統(tǒng)計(jì)[14]
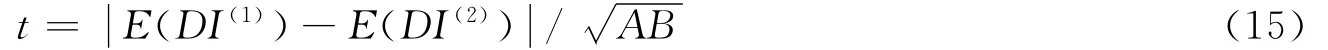
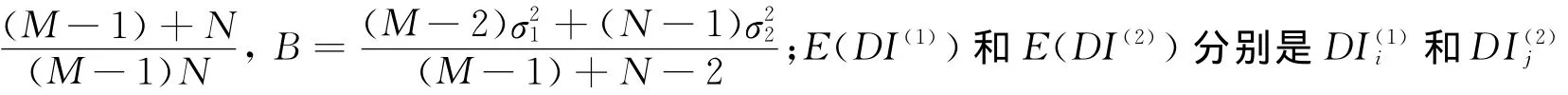
3.2 成像算法
將損傷情況可視化,定量確定損傷的位置,識(shí)別損傷的程度一直是結(jié)構(gòu)損傷識(shí)別研究的熱點(diǎn)問(wèn)題之一。本文中通過(guò)改進(jìn)T.R.Hay等[16]提出的RAPID(reconstruction algorithm for probabilistic inspection of damage)算法來(lái)進(jìn)行損傷成像研究。以損傷指標(biāo)代替原算法中的信號(hào)差別系數(shù)(signal difference coefficient,SDC),改進(jìn)后算法公式如下
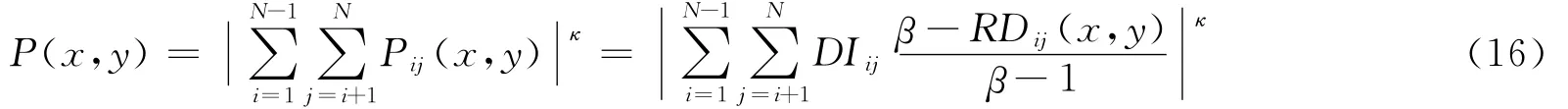
式中:β為尺寸參數(shù),大小為橢圓系最外面橢圓離心率的倒數(shù)。在本文中,為提高損傷區(qū)域的對(duì)比度,引入一個(gè)對(duì)比增強(qiáng)因子κ。
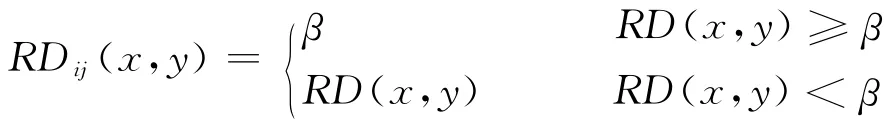
其中
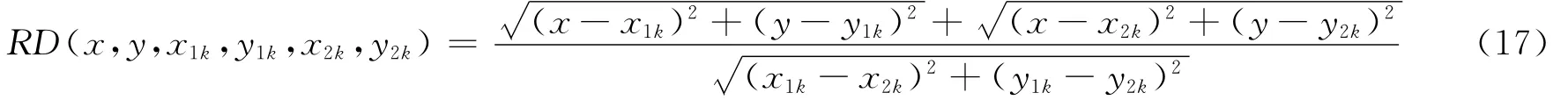
式(17)表示(x,y)坐標(biāo)處到發(fā)射和接收傳感器距離之和與發(fā)射接收傳感器間直接距離之比。圖4為傳感器通道示意圖,當(dāng)點(diǎn)(x,y)落在橢圓內(nèi)時(shí),RD(x,y)由式(17)計(jì)算得到;而當(dāng)點(diǎn)(x,y)超出橢圓系范圍,取RD(x,y)=β。本文中β=1.02,主要考慮直接路徑上的損傷。
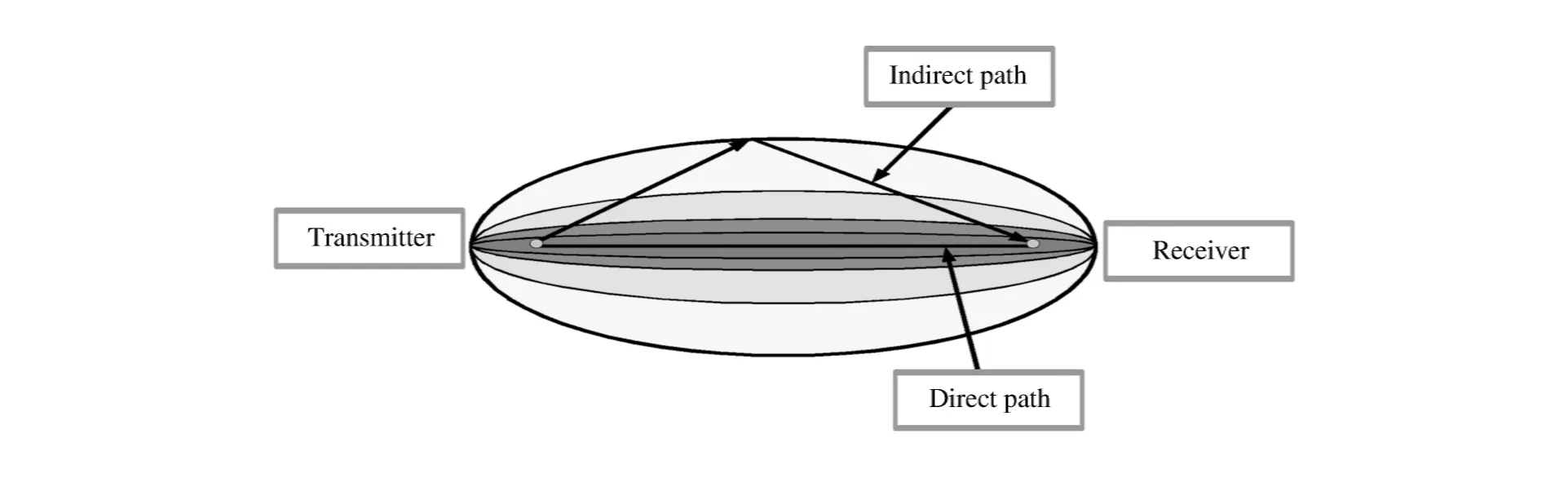
圖4 RAPID算法的傳感器通道示意圖Fig.4Illustrations of the elliptical distribution function of the RAPID algorithm
4 實(shí) 驗(yàn)
為驗(yàn)證本文中所提方法的可行性和有效性,建立在實(shí)驗(yàn)室條件下的結(jié)構(gòu)健康監(jiān)測(cè)系統(tǒng),整個(gè)系統(tǒng)由NI-PXI 6115數(shù)據(jù)采集卡和NI-PXI 5412信號(hào)發(fā)生器組成。試件為碳纖維復(fù)合材料板結(jié)構(gòu),尺寸為250mm×250mm×2mm,在結(jié)構(gòu)中預(yù)制沖擊損傷,造成復(fù)合材料板結(jié)構(gòu)中有纖維斷裂和脫層。
采用粘貼在結(jié)構(gòu)表面的壓電陶瓷元件來(lái)激勵(lì)和接收應(yīng)力波信號(hào)。在試件表面以板中心為圓心,在直徑15cm的圓上均勻布置12個(gè)直徑12mm、厚1mm的壓電傳感器S1~S12,組成一個(gè)如圖5所示的圓形傳感器監(jiān)測(cè)網(wǎng)絡(luò),用于損傷的監(jiān)測(cè)和成像實(shí)驗(yàn)。任意2個(gè)壓電傳感器就可以組成一條激勵(lì)-接收通道,共有66個(gè)激勵(lì)-接收路徑。試件及傳感器布置如圖6所示。
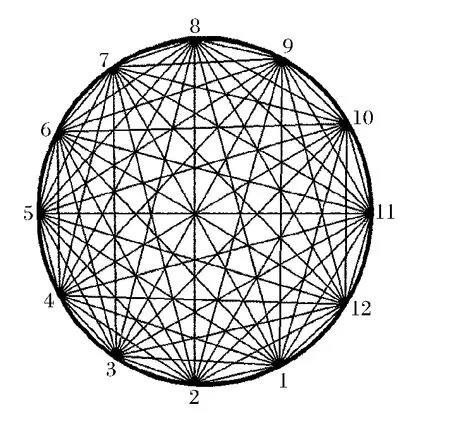
圖5 傳感器路徑示意圖Fig.5Diagram of sensing path

圖6 復(fù)合材料實(shí)驗(yàn)件Fig.6Composite plate and PZT
實(shí)驗(yàn)中由一個(gè)壓電傳感器在試件中激發(fā)窄帶Lamb波
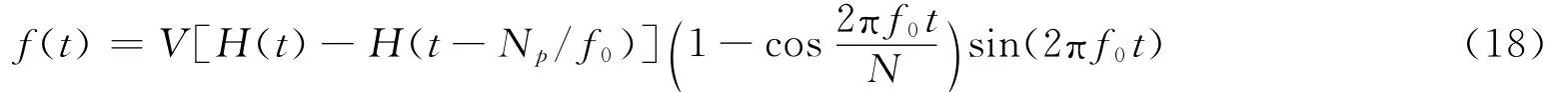
式中:V是信號(hào)幅值,H(t)是階躍函數(shù),Np是峰數(shù),f0是中心頻率。實(shí)驗(yàn)中窄帶波信號(hào)的中心頻率設(shè)定在200kHz。
首先在結(jié)構(gòu)無(wú)損傷狀態(tài)下測(cè)得1組Lamb波信號(hào)作為基準(zhǔn)信號(hào),再每隔0.5h(溫度、濕度和噪聲等環(huán)境發(fā)生變化)測(cè)量1次,測(cè)得10組信號(hào);然后在結(jié)構(gòu)有損傷狀態(tài)下同樣測(cè)得10組Lamb波信號(hào)作為監(jiān)測(cè)信號(hào),以傳感器路徑3-9(通過(guò)損傷)和路徑1-6(未通過(guò)損傷)為例,如圖7所示。

圖7 基準(zhǔn)及監(jiān)測(cè)狀態(tài)測(cè)得的Lamb波信號(hào)Fig.7Captured Lamb wave signals of the reference and present states
運(yùn)用本文中提出的損傷指標(biāo)提取方法,采用MP分析手段做預(yù)處理。選取150~250kHz這一頻帶作為尺度,分別對(duì)兩種狀態(tài)下的信號(hào)進(jìn)行時(shí)頻變換,得到信號(hào)的局部時(shí)間-能量密度,同樣以傳感器通過(guò)損傷路徑3-9和未通過(guò)損傷路徑1-6為例,如圖8所示,通道1-6的損傷指標(biāo)DI=0.026,通道3-9損傷指標(biāo)DI=0.963。
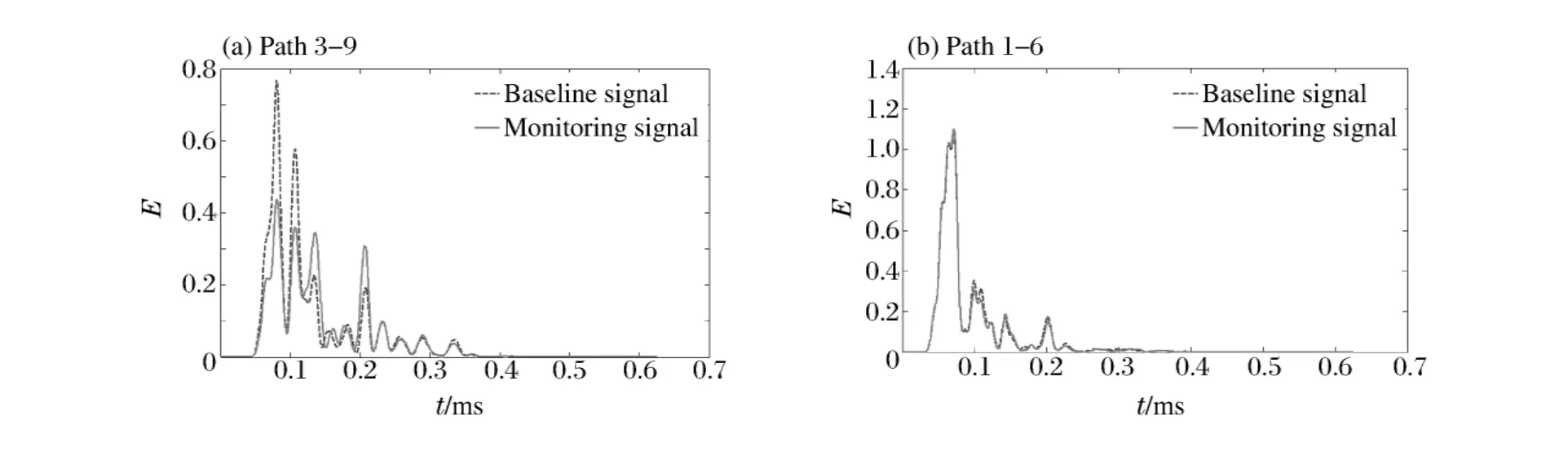
圖8 時(shí)間-能量密度圖Fig.8Diagram of local time-energy density
為了判斷損傷指標(biāo)是由結(jié)構(gòu)損傷引起還是因環(huán)境變化造成的,用概率統(tǒng)計(jì)方法對(duì)每條傳感器路徑上的損傷指標(biāo)進(jìn)行統(tǒng)計(jì)分析。實(shí)驗(yàn)中,置信度取為0.975,則t0.975=2.4。由此可見(jiàn),損傷指標(biāo)是由結(jié)構(gòu)損傷引起的,表1為損傷系數(shù)最大的12個(gè)通道。

表1 損傷系數(shù)最大的12個(gè)通道Table 1The maximum damage index of 12paths
將66個(gè)損傷指標(biāo)帶入RAPID算法,得到損傷圖像。圖9(a)、(b)為增強(qiáng)因子κ=1,5時(shí)的損傷圖像。圖中對(duì)比度最大的像素點(diǎn)即為識(shí)別出的損傷中心位置。圖9(c)為超聲C掃描的實(shí)際損傷圖像。通過(guò)對(duì)比可以看出,該算法得到的損傷圖像與實(shí)際損傷位置比較接近,得到的損傷圖像對(duì)比度高,對(duì)損傷的指示比較明顯。引入的對(duì)比度增強(qiáng)因子顯著提高了損傷區(qū)的相對(duì)對(duì)比度,大大提高了損傷定位的精度,且具有識(shí)別損傷尺寸的潛力。

圖9 增強(qiáng)因子κ=1,5時(shí)的損傷圖像和超聲C掃描圖像Fig.9The damage image when the image factorκ=1,5and the actual damage image using ultrasonic C scan
5 結(jié) 論
對(duì)采用壓電傳感器網(wǎng)絡(luò)的復(fù)合材料結(jié)構(gòu)健康監(jiān)測(cè)系統(tǒng)進(jìn)行了研究,提出了一種基于Lamb波匹配追蹤算法時(shí)頻處理的損傷概率成像方法。對(duì)復(fù)合材料結(jié)構(gòu)中的Lamb波信號(hào),使用匹配追蹤算法進(jìn)行時(shí)頻分析,提取損傷特征值,運(yùn)用損傷概率成像算法即RAPID算法進(jìn)行損傷成像,將損傷情況可視化,為定量確定損傷的位置、識(shí)別損傷的程度提供一種快速直觀的方法,但還需進(jìn)行深入的研究考慮損傷尺寸對(duì)散射lamb波的影響,使得到的損失圖像能準(zhǔn)確指示損傷的大小和程度。
[1]Giurgiutiu V,Cuc A.Embedded NDE for structural health monitoring,damage detect ion,and failure prevention[J].The Shock and Vibration Digest,2005,37(2):83-105.
[2]Su Z,Ye L,Lu Y.Guided Lamb waves for identification of damage in compo site structures:A review[J].Journal of Sound and Vibration,2006,295(4):753-780.
[3]Wang C S,Chang F K.Diagnosis of impact damage in composite structures with built-in piezoelectrics network[C]∥Proceedings of the SPIE,Smart Structures and Materials.San Diego,CA:SPIE,2000:13-19.
[4]Cawley P,Alleyne D.The use of Lamb waves for the long range inspect ion of large structures[J].Ultrasonics,1996,34(2):287-290.
[5]嚴(yán)剛,周麗.基于Lamb波的復(fù)合材料結(jié)構(gòu)損傷成像研究[J].儀器儀表學(xué)報(bào),2007,28(4):583-589.
YAN Gang,ZHOU Li.Study on damage imaging for composite structure using Lamb wave[J].Chinese Journal of Scientific Instrument,2007,28(4):583-589.
[6]Hay T R,Wei L,Rose J L,et al.Rapid inspection of composite skin-h(huán)oneycomb core structures with ultrasonic guided waves[J].Journal of Composite Materials,2003,37(10):929-939.
[7]Howard M M,Lanza di Scalea F.Macro-fiber composite piezoelectric rosettes for acoustic source location in complex structures[J].Smart Materials and Structures,2007,16(4):1489-1499.
[8]Swartz A,F(xiàn)lynn E,Backman D,et al.Active piezoelectric sensing for damage identification in honeycomb composite panels[C]∥Proceedings of 24th International Modal Analysis Conference.Los Alamos National Laboratory,2006.
[9]Ihn J B,Chang F K.Pitch-catch active sensing methods in structural health monitoring for aircraft structures[J].Structural Heath Monitoring,2008,7(1):5-19.
[10]Deng X M,Wang Q,Giurgiutiu V.Structural health monitoring using active sensors and wavelet transforms[C]∥Proceedings of the SPIE,Smart Structures and Integrated Systems.Newport Beach,USA:SPIE,1999:363-370.
[11]Quek S T,Tua P S,Wang Q.Detecting anomalies in beams and plate based on the Hilbert-Huang transform of real signals[J].Smart Materials and Structures,2003,12(3):447-460.
[12]Hong J C,Sun K H,Kim Y Y.Dispersion-based short-time Fourier transform applied to dispersive wave analysis[J].Journal of the Acoustical Society of America,2005,117(5):2949-60.
[13]Mallat S G,Zhang Z.Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415.
[14]Banerjee S,Ricci F,Monaco E,et al.A wave propagation and vibration-based approach for damage identification in structural components[J].Journal of Sound and Vibration,2009,332(1/2):167-183.
[15]Monaco E,F(xiàn)ranco F.Experimental and numerical activities on damage detection using magnetostrictive actuators and statistical analysis[J].Journal of Intelligent Material Systems and Structures,2000,11:567-578.
[16]T R Hay,R L Royer,Huidong Gao,et al.A comparison of embedded sensor Lamb wave ultrasonic tomography approaches for material loss detection[J].Smart Materials and Structures,2006,15(2):946-951.

