Artificial neural network modeling of mechanical properties of armor steel under complex loading conditions

XU Ze－jian（許澤建）， HUANG Feng－lei（黃風雷）

（State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing 100081，China）

Widely used in armor protection systems due to their high strength and toughness，armor steels are often subjected to extreme loading conditions such as crash，impact，or explosion in their service environments.The ballistic resistance performance of armor steel is directly related to its mechanical properties under conditions of high strain rate，high temperature，and large plastic strain.Therefore，a thorough understanding of the plastic behaviors and the constitutive relationship modeling under such conditions are needed for the design of the components in its application.In our previous work［1］，mechanical behaviors of the 603armor steel were studied systematically over wide temperature and strain rate ranges.Based on the results，two phenomenological constitutive models，as well as five physically based ones have been established to describe and predict the plastic behaviors of this material.

In recent years，the artificial neural network（ANN）approach has been introduced into the field of materials science as a powerful mathematical modeling technique and found growing application in materials property determination［2－8］.Several studies were conducted［9－12］using ANN to predict flow stress of alloys in hot deformation or hot forging cycles at restricted temperature or strain rate ranges.However，few studies are recordable in scientific literature that utilize ANN to describe material behavior at strain rates ranging from quasi－static to dynamic，with different deformation temperatures.Moreover，the predictive capabilities of the established ANN models were rarely verified.

In this work，constitutive relationship of the 603armor steel is established over wide ranges of strain rate and temperature，using a three－layer feed－forward ANN with a back－propagation （BP）learning algorithm.Validity of this ANN model is checked by the strain rate jump tests.Descriptive and predictive capabilities of this approach are compared with other constitutive models that were built on the same experimental data.

1 Material and experimental procedure

The 603steel was hot rolled and subsequently subjected to recrystallization and annealing.All the cylindrical samples are machined from a baseplate.The samples have a 6mm nominal diameter and 9mm height for quasi－static experiments，while in case of dynamic loading，the samples are 5 mm in diameter and 4mm long.

The quasi－static compression tests under strain rates of 0.001s－1and 1s－1are performed using an MTS hydraulic testing machine.The dynamic compression tests，with strain rates of 200s－1，2 000s－1，and 4 500s－1，are conducted using the revised split Hopkinson pressure bar（SHPB）technique［13］.For both quasi－static and dynamic tests，the elevated temperatures，including 473K，673Kand 873K，are attained with electro－thermal cells.After that，a three－step strain rate jump test is carried out，to assess the validity of the established ANN model.

2 ANN approach

An ANN is made up of interconnected computational elements known as nodes or neurons to simulate the processes that occur in the human brain and nervous system during pattern recognition，information filtering and functional control.ANN can learn from example data and construct an input－output mapping，producing reasonable outputs for new inputs.This technique is particularly suitable for modeling non－linear problems involving the manipulation of multiple parameters and interpolation，such as the combined effects of strain rate，temperature，and strain on flow stress.A－mong various ANN approaches that have been proposed，the multi－layer perceptron（MLP）architecture with a BP algorithm has been used most wide－ly.MLP based neural networks are made up of layers of neurons with suitable weighted interconnections，forming a feed－forward topology in the hierarchical structure.The input and output layers consist of different numbers of neurons，depending on the numbers of the input and output variables in the model，respectively.In the feed forward process，the input data are presented to input layer neurons that pass the input values onto the first hidden layer and so on.Each of the hidden layer nodes computes a weighted sum of its input.This sum is then passed through the transfer function and the final results are obtained at the output layer.The outputs are compared with the target results，and the total error energyE（n）at iteration numbernfor all thePneurons in the output layer is calculated by

wheredj（n）is the target output for neuronjat iterationnandyj（n）is the network output of neuronjat iterationn.The BP algorithm is used to adjust network weights and biases according to the transmitted backward error information to minimize the errors between the predicted and actual outputs.This process is operated iteratively to train the network until a specified convergence is reached.In this study，a three－layer MLP neural network with a BP learning algorithm is used to simulate plastic behaviors of the 603armor steel.The structure of our neural network is schematically shown in Fig.1.The inputs of the ANN model are plastic strain，log strain rate，and deformation temperature，while the output is flow stress.The design and training of the ANN model is performed using the neural network toolbox of the MATLAB software. Here the Levenberg－Maquarolt algorithm is used to train the network for fast optimization.

Fig.1 Schematic structure of the ANN model

Experimental data of the 603armor steel obtained from compression tests are used to develop the ANN model.In those tests，the initial temperatureT0ranges from 288Kto 873K （288K，473K，673K，and 873K），the strain rateranges from0.001s－1to4 500s－1（0.001s－1，1s－1，200s－1，2 000s－1，and4 500s－1），andtheplastic strainεrangesfrom0to0.45.Fordynamictests（200－4 500s－1），theadiabatictemperaturerise inthematerialduringplasticdeformationisconsidered，whichiscalculatedby

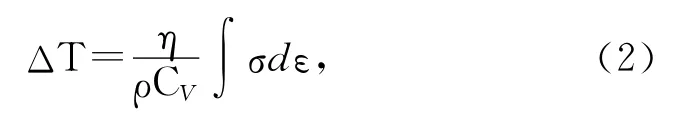
whereσisflowstress（MPa），ρisthemassdensity（7.8g／cm3），CVistheheatcapacity（0.48J／（g·K）），andηisthefractionofplasticwork convertedintoheat.Inthepresentstudy，ηis takentobe1.Foreachtestunderdynamicloading，ΔTis firstly calculated for each specific value ofε，andthenthedeformationtemperatureT（＝T0＋ΔT）isusedinnetworktraining.Totally606datasets（ε，logε·，T，andσ）areemployedfrom thestress－straincurvestodeveloptheANNmodel.Beforenetworktraining，allthedatasetsarenormalizedtotransformthevaluesbetween－1and1toincreasetheefficiencyofthenetworkandto minimizetheeffectsofmagnitudevariationin thedata.

Todetermineanappropriatehiddenlayer，a seriesofANNmodelshavebeendevelopedwith thehiddenlayerneuronsrangingfrom1to20.Thegeneralizationcapabilityofthetrainednetworksischeckedbymeansquareerror（MSE）and correlationcoefficient（R）basedonthetargetand outputvaluesbytheequations：

whereNis the total number of the employed datasets，diandyiare target and network output values respectively，Eis the experimental value，Pis the predicted value by the ANN model，andandPare the mean values ofEandPrespectively.From Fig.2it is observed that both MSE andRchange abruptly at first with the increase of the hidden layer neurons.However，when more than 4 neurons are used，MSE andRchange at a much lower rate.After the neuron number exceeds 11，the values of MSE andRreach a comparatively stable state，and improvement in the network performance is not obvious with further increase of neurons.Therefore，11neurons are used in the hidden layer of our ANN model，in consideration of the network performance and the computation cost.The details of network topology and training parameters are shown in Tab.1.

Fig.2 Network performance variation with neurons in the hidden layer

3 Results and discussion

3.1 Model performance

In network training，both the input and target vectors are randomly divided into 3sets：60%are used for training，20%are used to validate that the network is generalizing and to stop training before overfitting，and the last 20%are used as a completely independent test of network generalization.The performance of the network at each epoch of training is also checked by MSE between experimental data and network output.Fig.3shows the variation of MSE with increasing training epochs.As can be seen，the best performance is achieved at epoch 38，with MSE＝0.002 859.The corresponding correlation coefficient at this epoch is 0.994 1.With the trained ANN model，the description of plastic behavior of the 603armor steel at different loading conditions is presented in Fig.4.It is observed that the model prediction can precisely simulate the plastic behaviors of the material at each specific strain rate and temperature level.For dynamic tests，the oscillations of the experimental data are not characterized by this ANN model，which describes the flow stress with comparatively smooth curves.

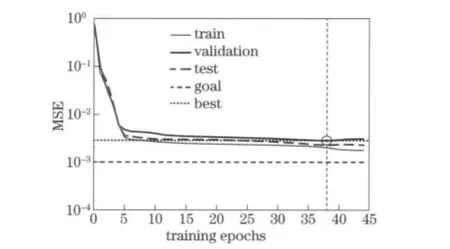
Fig.3 Variation of ANN model performance with increasing training epochs

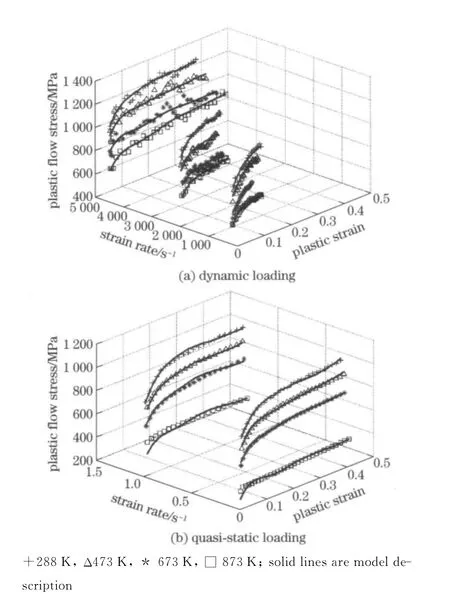
Fig.4 ANN model description of plastic behavior of the 603armor steel at different loading conditions

In Fig.5，plastic flow stress for plastic strain levels ranging from 0.02to 0.14at strain rate of 2 000s－1are plotted with the experimental temperature.The adiabatic temperature rise for each strain level is also considered here，which can be observed from the inclination of the experimental data with the increase of plastic strain.With the increase of initial temperature，the plastic flow stress decreases for each plastic strain，with a decreasing rate.As can be seen，the temperature effect of the flow stress can be described quite well by the ANN model，including the lower rate of the decreasing at a higher initial temperature.Variation of plastic flow stress with strain rate at a constant strain level of 0.1for tests performed at different initial temperatures are shown in Fig.6.At the beginning，the flow stress increases slowly with a linear relationship relative to strain rate，and then increases rapidly when the strain rate is above 200s－1.This variation of strain rate sensitivity can also be described successfully by the ANN model for each initial temperature.The correlation between the experimental data and the predicted results is shown in Fig.7，withR＝0.994 1.

3.2 Predictive capability verification

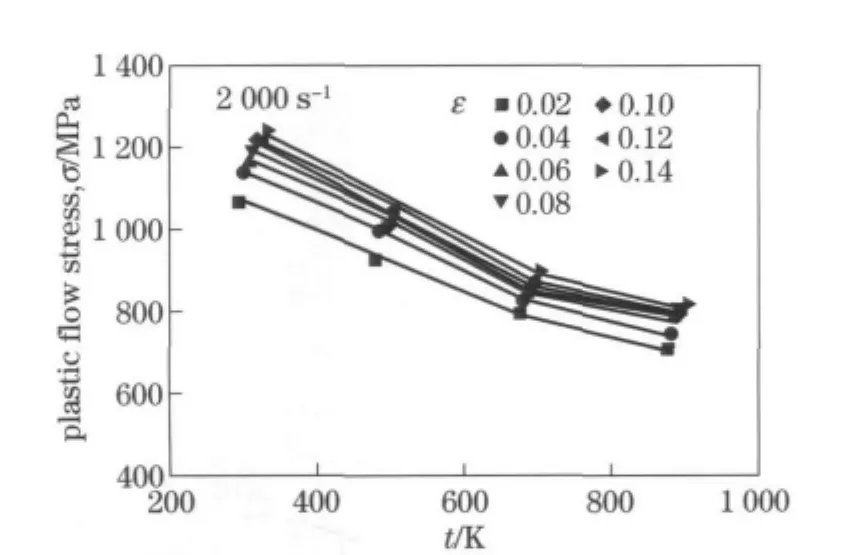
Fig.5 ANN model description of the temperature effect on plastic flow stress

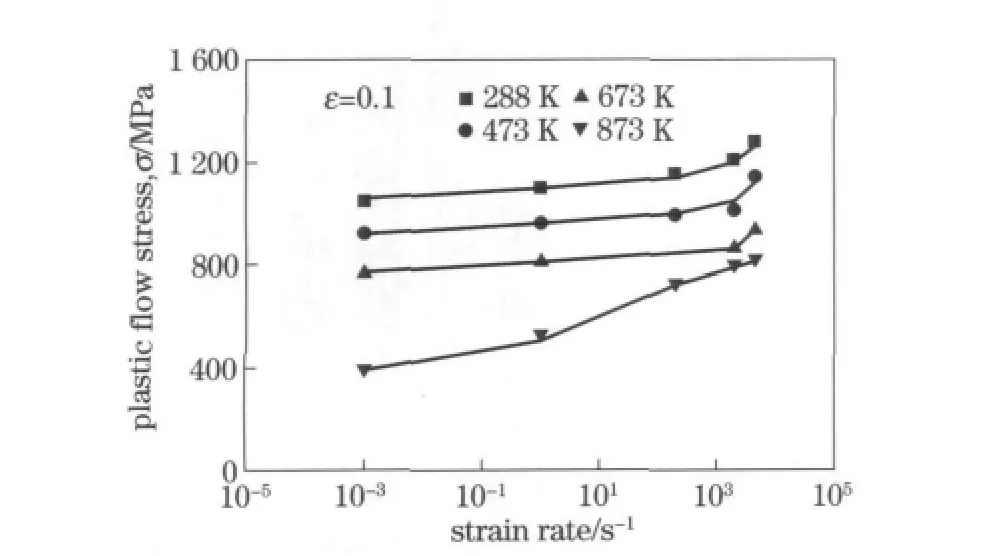
Fig.6 ANN model description of the strain rate effect on plastic flow stress

Fig.7 Correlation between the experimental and ANN predicted values for the training data

For verification of its predictive capability，the obtained ANN model is used to simulate the strain rate jump tests，which were not included in the development of the neural network.A sample used for quasi－static test was firstly loaded to a plastic strain of 13.6%at 753Kand 0.002s－1，then the initial temperature was decreased to 533Kand the sample was compressed sequentially to plastic strain 23.2%at 0.48s－1.After that，the sample was machined to 4mm both in diameter and length，and then tested using the SHPB technique at 293Kand 4 300s－1，to plastic strain 61.4%.In the model prediction，adiabatic temperature rise ΔTis only considered in the third loading step，while the first two steps are assumed to be under isothermal conditions.Isothermal results are firstly obtained by the ANN model for all the three loading steps，thenΔTis calculated according to the predicted flow stress in the third loading step，and new input datasets are obtained with deformation temperatureT.With the newly generated input vectors，the flow stress of the third loading step is predicted again.Both the isothermal and the final results are shown in Fig.8.The points represent experimental results，while the lines are predicted values by the ANN model withTorT0.

From Fig.8，the ANN model prediction is in good agreement with the experimental results under the condition of 753Kand 0.002s－1.But for the subsequent loading step，the ANN model gives higher predictions than the measured values.In the third loading step，it is important to note that with consideration of adiabatic temperature rise the predictive capability of the ANN model is evidently improved.By using deformation temperatureT，it gives a much better prediction to the descending trend of the flow stress，which results from generation of a large amount of heat during fast deformation of the material.Therefore，the adiabatic temperature rise in dynamic tests is handled properly both in the developing of the model and in the prediction procedure.The MSE of all the three experimental steps is 0.052 4，andR＝0.969.

In our previous work，the descriptive and predictive capabilities of two phenomenological constitutive models（JC and KHL）［1］，and five physically based models（PB，NNL，ZA，VA，and RK）［2］were investigated based on the same experimental data.For comparison，here we also measure the average absolute relative error（AARE）between the ANN model characterization and the experi－mental results by the following relation

whereσexpandσmodelareflowstressfromexperimentsandANNmodel，respectively.According toEq.（5），thedescriptionerrorsforthetraining dataare1.51%and2.05%，forthequasi－static anddynamicconditionsrespectively.Forthe strainratejumptests，thepredictionerrorateach conditionis13.7%and9.9%，respectively.The descriptiveandpredictiveerrorsareshownin Fig.9，togetherwiththeaveragevalueofthe quasi－staticanddynamictestsforeachconstitutive model.Ascanbeseen，thedescriptiveerrorofthe ANNmodelismuchlowerthanthatofallthe othermodels，forbothoftheloadingconditions.ThisperformanceoftheANNmodelindescribingthetrainingdataindicatesitssuperiorflexibilityinthesimulationofhighlynonlinearthermoviscoplasticresponsesofmaterials.Forthe strainratejumptests，theaveragevalueofthe quasi－staticanddynamicerrorsoftheANNmodelis11.80%.Itspredictivecapabilityisbetter thantheNNL，ZA，RK，andJCmodels，of whichtheaverageerrorsare12.27%，13.30%，14.94%，and14.97%respectively.Fortherest models，theaverageerrorsarePB8.74%，VA9.93%andKHL9.83%.Theresultsshowthata properlytrainedneuralnetworkmayserveasa validandeffectivetooltocharacterizeplasticbehaviorsofthe603steeloverwiderangesoftemperaturesandstrainrates.

Fig.8 Comparison between the measurement and ANN model prediction for strain rate jump tests

Fig.9 Comparison of the ANN model performance with other constitutive models

4 Conclusion

Athree－layerMLPANNwithaBPlearning algorithmisestablishedtosimulateplasticbehaviorsofthe603armorsteeloverwiderangesof temperaturesandstrainrates.Boththedescriptive andthepredictivecapabilitiesofthedeveloped ANNmodelarechecked，andcomparedwithotherconstitutivemodels.TheANNmodelhasa muchbetterapplicabilitythantheothermodelsin characterizationofthebasicexperimentaldata.Boththetemperatureandthestrainrateeffectson theflowstresscanbedescribedsuccessfullyby thismodel.Inthepredictionoftheflowstressin thestrainratejumptests，theANNmodelexhibitsabetteraccuracythanmostoftheothermodels，withanaverageerrorof11.80%fortheboth loadingconditions.Amajoradvantageofthe ANNmodelistheconvenienceinmodelestablishmentanddataprocessing，besidesitsoutstanding performanceindescriptionofthetrainingdata andaconsiderableprecisioninprediction.There－sultsshowthattheANNmodelthatisdeveloped heremayserveasavalidandeffectivetoolto characterizeplasticbehaviorsofthe603steelundercomplexloadingconditions.

［1］Xu Z J，Huang F L.Comparison of physically based constitutive models characterizing armor steel over wide temperature and strain rate ranges［J］.Modelling and Simulation in Materials Science and Engineering，2012，20：015005.

［2］Rusinek A，Rodríguez－Martínez J A，Arias A.A thermo－viscoplastic constitutive model for FCC metals with application to OFHC copper ［J］.Int J Mech Sci，2010，52：120－135.

［3］Rao K P，Prasad Y K D V.Neural network approach to flow stress evaluation in hot deformation［J］.J Mater Process Tech，1995，53：552－566.

［4］Liu Q，Ji Z，Liu M，et al.Acquiring the constitutive relationship for a thermal viscoplastic material using an artificial neural network ［J］.J Mater Process Tech，1996，62：206－210.

［5］Hwu Y J，Pan Y T，Lenard J G.A comparative study of artificial neural networks for the prediction of constitutive behaviour of HSLA and carbon steel ［J］.Steel Res，1996，67：59－66.

［6］Chun M S，Biglou J，Lenard J G，et al.Using neural networks to predict parameters in the hot working of aluminium alloys［J］.J Mater Process Tech，1998，86：245－251.

［7］Sumantra Mandal，Sivaprasad P V，Venugopal S.Capability of a feed－forward artificial neural network to predict the constitutive flow behavior of as cast 304 stainless steel under hot deformation ［J］.Trans ASME J Eng Mater Technol，2007，129：242－247.

［8］Lin Y C，Zhang J，Zhong J.Application of neural networks to predict the elevated temperature flow behavior of a low alloy steel［J］.Comput Mater Sci，2008，43：752－758.

［9］Bariani P F，Bruschi S，Dal Negro T.Prediction of nickel－base superalloys’rheological behaviour under hot forging conditions using artificial neural networks［J］.J Mater Process Tech，2004，152：395－400.

［10］Edwin Raj R，Daniel B S S.Prediction of compressive properties of closed－cell aluminum foam using artificial neural network ［J］.Comput Mater Sci，2008，43：767－773.

［11］Sun Y，Zeng W D，Zhao Y Q，et al.Development of constitutive relationship model of Ti600alloy using artificial neural network ［J］.Comput Mater Sci，2010，48：686－691.

［12］Ji G，Li F，Li Q，et al.Prediction of the hot deformation beharior for Aermet100steel using an artificial neural network［J］.Comput Mater Sci，2010，48：626－632.

［13］Nemat－Nasser S，Isaacs J B，Starrett J E.Hopkinson techniques for dynamic recovery experiments［J］.Proc R Soc Lond，1991，A435：371－391.

（Edited byWang Yuxia）