DSA250型受電弓振動特性仿真與測試
李東陽,吳積欽,關金發
0 引言
近年來國內高速鐵路飛快發展,隨著列車速度的提高,受電弓與接觸網關系的問題日益突出。動車組是通過受電弓從接觸網上獲取電能,所以良好的弓網接觸是保證列車取流的必要條件,列車運行時如何保證良好的受流質量,已經成為高速鐵路技術的重要問題。而弓網動力學作為高速鐵路弓網關系問題研究的核心,是影響弓網接觸質量的關鍵因素之一。良好的弓網動態特性,對受電弓的動力學性能提出了較高的要求。
受電弓的固有振動反映其固有的動力學特性,是研究其振動問題的基礎。受電弓在列車行駛的過程中產生復雜的振動,其振動狀況直接影響列車受流質量。對受電弓進行固有頻率的計算和測試,對優化受電弓結構和接觸網設計有重要的意義。本文分別用質量塊模型和實體模型對高速受電弓的動態特性進行了研究,最后用實驗手段進行了測試,并把實驗數據和仿真數據進行對比分析。
1 受電弓的結構與計算模型
DSA250型受電弓近年來廣泛用于高速鐵路動車組,它由弓頭、框架、底架和傳動機構4部分組成,框架包括上導桿、上臂桿、下臂桿和下導桿等桿件,各桿件用鉸接相連。弓角的材料為鈦合金,上臂桿、下臂桿都由高強度鋁合金制作,下導桿為不銹鋼材料,底架為鋼材料,整弓重量約115 kg。底架通過絕緣子固定在車頂上,框架通過升弓裝置支持弓頭,傳動機構作用于下臂桿實現升弓動作。氣動升弓裝置安裝在底座上,通過鋼絲繩作用于位于下臂桿下部的線導板,從而實現升弓過程。碳滑板安裝在弓頭支架上,弓頭支架垂懸在4個拉簧下方,設計速度為250 km/h[3]。
為分析受電弓的動態特性,可采用質量塊模型和實體模型2種方法。下面分別用質量塊模型和實體模型建模,求解DSA250型受電弓的固有頻率。
1.1 質量塊模型
由于在受電弓和接觸網動力學中,受電弓對接觸線的作用主要體現在垂直方向,所以可以對受電弓進行簡化,使其等效成只有垂向運動的彈簧—質量塊模型。國內外學者普遍把受電弓等效成兩質量塊和三質量塊模型,本文采用三質量塊模型等效DSA250型受電弓,質量塊之間通過彈簧和阻尼器耦合,如圖1所示。
在圖1中,m1、m2、m3分別為弓頭、上框架、下框架的等效質量,k1、c1為弓頭與上框架之間的等效剛度和阻尼,k2、c2為上框架與下框架之間的等效剛度和阻尼,k3、c3為下框架和底座之間的等效剛度和阻尼。
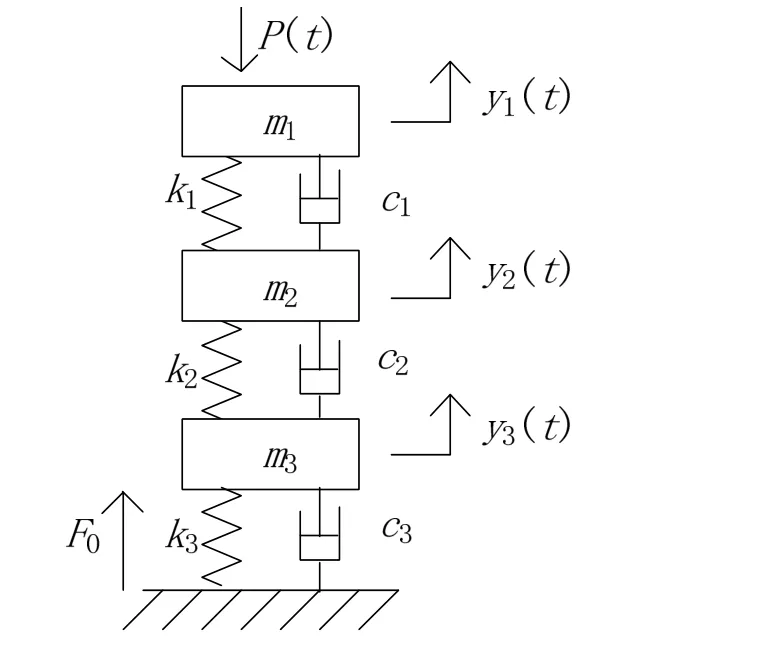
圖1 受電弓的三質量塊等效模型示意圖
三質量塊模型的動力學方程為
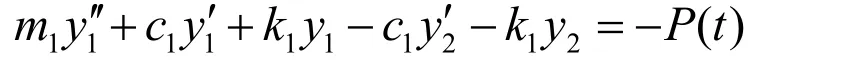
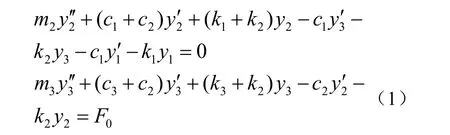
正常運行狀態下,主要參數的取值如表1。
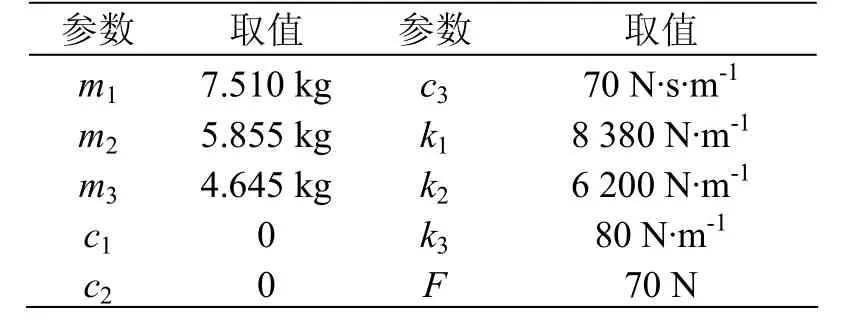
表1 DSA250受電弓歸算參數表
把參數帶入式(1),可得一組三元二次微分方程:

利用Simulink中的狀態空間模塊求解式(2),得出 3個質量塊的共振頻率分別為 0.36,5.38和9.74 Hz。
需要注意的是,在不同的升弓高度下,受電弓有不同的等效參數,受電弓在升弓高度分別為982,1 600,2 894 mm時,有不同的等效參數,其中升弓高度在982 mm時的數據如表2[6]。

表2 升弓高度為982 mm時受電弓的歸算參數表
將該組數據帶入動力學方程重新計算可得共振頻率分別為0.33,4.3和7.6 Hz。
質量塊模型參數少,計算方便,在分析弓網接觸質量的研究中,能反應受電弓的主要動態特征。
1.2 實體模型
利用有限元方法,可以對實體模型進行模態分析。已知通用運動方程
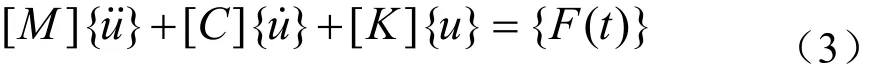
在模態分析中,物體做自由振動,在忽略阻尼的情況下
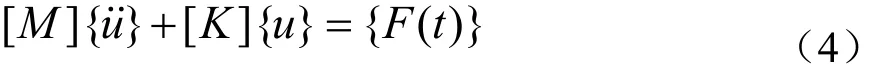
假定其為諧運動,于是有

Inventor是美國 AutoDesk公司推出的一款三維可視化實體模擬軟件,可以實現三維模型的創建和有限元仿真。在Inventor中搭建受電弓的實體模型,并對其進行模態分析,得出受電弓實體模型的各階模態見表3。
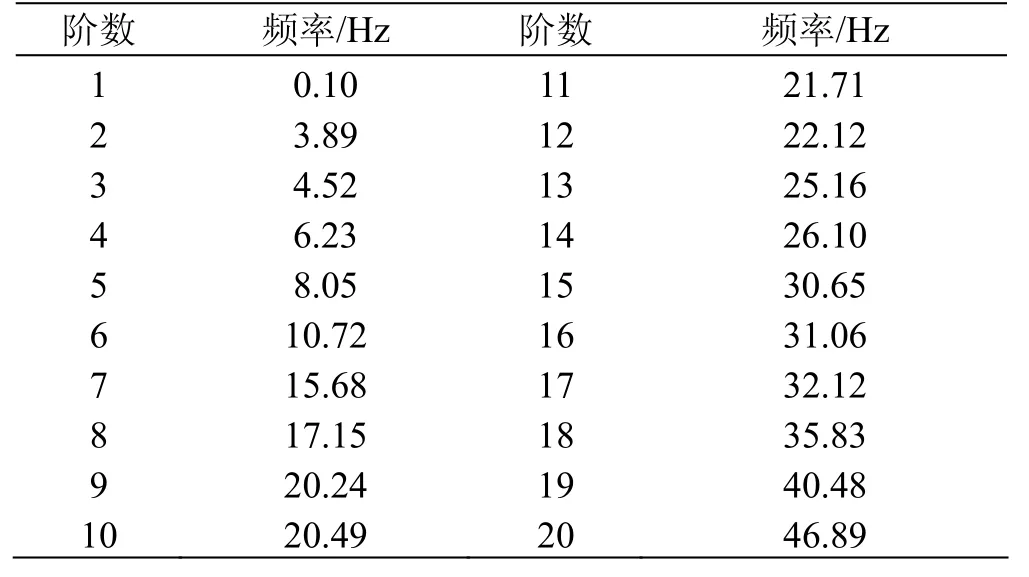
表3 升弓高度為982 mm時受電弓的整體模態表
圖2—圖4是頻率為0.1,4.52,8.05 Hz時的振型例圖。

圖2 頻率為0.1 Hz時受電弓的振型例圖
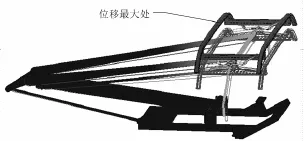
圖3 頻率為4.52 Hz時受電弓的振型例圖
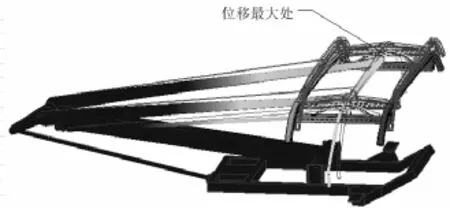
圖4 頻率為8.05 Hz時受電弓的振型例圖
可以看出,頻率為0.1 Hz時,受電弓的變形主要為下臂桿的垂向振動,頻率為4.52 Hz時,受電弓的變形主要為弓頭的垂向振動,頻率為 8.05 Hz時,受電弓的變形主要為上臂桿的垂向振動。
在對受電弓實體模型進行分析后發現,實體模型具有很多模態數,除了平時比較關心的垂向低頻模態,還反應出受電弓各部位在振動中各個方向的位移,以及在較高頻率下的振型,能更詳細地反應受電弓振動的真實狀況。
2 受電弓振動試驗
對受電弓進行動力學的實測,測得受電弓的模態,可以驗證仿真和計算模型的準確性。搭建受電弓振動試驗臺,實驗系統主要由激振系統、信號采集與放大、計算機+處理軟件3個部分組成。基本原理框圖如圖5所示。
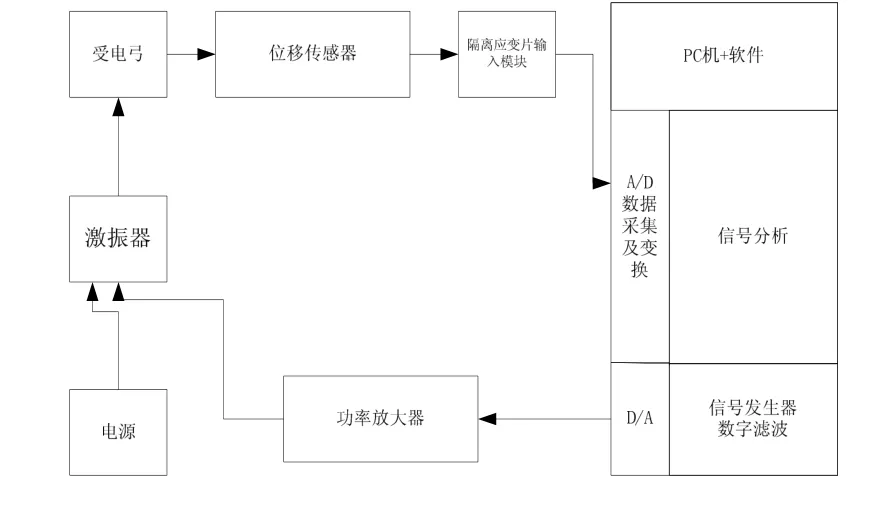
圖5 受電弓試驗臺原理框圖
實驗選用的位移傳感器最大量程為100 mm,精度為千分之一,接口為四線制,2根是DC 24 V的電源線,2根是信號線,輸出0~10 V的數據,延長線為1 m,以便安裝在受電弓上。關注的受電弓振動頻率范圍為 0~12 Hz,該實驗把信號發生器的頻率從0調節到12 Hz,激振器在弓頭處給受電弓施加位移,安裝在受電弓弓頭上的傳感器輸出信號通過模塊采集并在計算機里生成數據文件。圖6是激振頻率為5 Hz時的弓頭位移曲線圖。

圖6 使用5 Hz頻率激振時的弓頭位移曲線圖
調節激振器的頻率從1~12 Hz(每隔0.1 Hz采集一次),記錄下每一個頻率下的振幅,做出幅頻曲線如圖7所示。
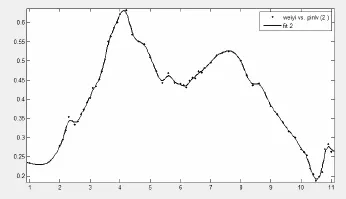
圖7 弓頭的幅頻特性曲線圖
從實測受電弓的幅頻曲線可看出,受電弓在4.5 Hz和7.8 Hz左右振幅最大,而由于該實驗采用的激振器無法產生1 Hz以下信號,故未測出0.3 Hz左右的振幅。
3 結論
通過質量塊模型計算出 DSA250型受電弓在升弓高度為982 mm時的固有頻率為0.33,4.30,7.60 Hz。通過有限元軟件的模態仿真得出的模態數眾多,但在0.33,4.30,7.60 Hz 3個頻率附近弓頭、上框架和下框架在垂向有較大位移。實驗測得頻率在 1~12 Hz,弓頭的共振頻率為 4.50和7.80 Hz。3種方法得出的結果可以得到互相驗證。
如果能建立準確的有限元模型,能比實驗更方便地測得受電弓的模態數據。因為在實驗中,很難測得受電弓各個部位在各個方向的位移,而這些在有限元軟件中能直觀地反應出來,能節省大量的人力物力。如果進行弓網動力學分析,為了控制計算量,則最好使用質量塊模型。
[1]李德葆.工程振動試驗分析[M].北京:清華大學出版社,2004.
[2]李敏,李豐良,馬俊.高速受電弓的力學模型及運動微分方程[J].鐵道科學與工程學報,2005,(6):83-87.
[3]馬果壘.受電弓系統研究[D].西南交通大學碩士研究生學位論文,2009.
[4]梅桂明.受電弓-接觸網系統動力學研究[D].西南交通大學博士研究生學位論文,2010.
[5]周寧,張衛華,王冬.受電弓等效模型參數識別及動態性能測試[J].西南交通大學學報,2011,(6):398-403.
[6]梅桂明,張衛華.受電弓/接觸網系統動力學模型及特性[J].交通運輸工程學報,2002,(1):20-25.

