配電網中光伏微網系統的新型控制策略

夏向陽 萬 成

（長沙理工大學電氣與信息工程學院，長沙 410114）

隨著全球經濟的飛速發展以及石化能源的過度消耗，環境及能源問題已經變得十分嚴峻。具有清潔、可持續使用的太陽能被公認為是當今國內外最具發展潛力的新能源[1-2]。隨著人們對環境保護與節能減排的日益關注，光伏微網系統的大規模生產和投入使用已經成為一種趨勢。

與傳統的發電方式相比，太陽能光伏發電具有清潔干凈、時間長久、獲取方便、數量巨大等優點[3]。目前，國內各大太陽能光伏發電設備生產廠家，如無錫尚德、常州天合、中電電氣（南京）、北京清華陽光能源隨之也相繼宣布太陽能光伏微網系統研究計劃。根據研究預計，2020年光伏發電量將占全球總發電量的1%左右，到2040年約占20%[4]。可見，光伏微網系統正在迅速進入電力能源結構，并且將逐步成為其不可或缺的一部分[5]。然而，隨著光伏發電大量進入系統，將對電網的穩定運行產生影響。傳統的無源濾波器已經不能滿足現在電力對電能質量的要求，因此，光伏并網裝置和有源濾波器（APF）相結合的復合控制成為近年來國內外研究的熱點[6]。

目前已有研究成果中，光伏并網運行時，并網瞬間整流裝置會對電網產生沖擊電流，運行時由于天氣原因使直流側電壓不穩定，產生電壓閃變，影響電網的安全運行，文獻[7]提出了對負載不穩定電流的抑制，卻沒有提出詳細的解決方案；文獻[8]基于有源電力濾波器，提出了用于直流側電壓控制的模糊PI控制方法，穩定性強，濾除諧波效果良好，但是響應速度緩慢，且沒有詳細分析有源電力濾波器濾波的控制策略。文獻[9]基于瞬時無功功率理論，提出了無功及諧波電流的檢測方法，但是沒有解決系統穩定性問題。文獻[10]給出了無功補償和光伏并網發電的統一控制方法，但是并沒有考慮負載側電流的不穩定因素，也沒有充分利用兩者的優點進行進一步的功能拓展。

基于此，本文綜合分析了應對濾除各次諧波的穩定復合控制策略。首先基于LCL型三相光伏微網系統的結構，分析了其工作原理，建立了濾波器的數學模型；然后，基于濾波器的數學模型，提出一種PI控制與無差拍控制相結合的復合控制策略。通過仿真證明：本論文提出的控制方案能有效提高光伏發電率，改善電網的電能質量，對確保電網的安全經濟運行有一定的作用。

1 組合系統結構及模型

1.1 主電路拓撲結構

本文的光伏微網系統基于三相對稱，其拓撲結構如圖1所示。主要組成部分有電源單元、逆變單元和LCL濾波單元。直流側二極管D防止電流逆流，電容C防止電壓突變。L1和L2為濾波電感，C1為濾波電容。

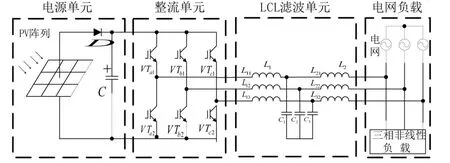
圖1 三相光伏微網系統的拓撲結構圖

1.2 LCL濾波器模型

在圖1中選擇電感L1上的電流i1，電感L2上的電流i2以及電容C1上的電壓Uc為狀態變量。如圖2所示，在三相平衡的情況下，由KCL和KVL定理可列出狀態方程，同時令直流側電壓為Uai，電網側電壓為Uao，則有

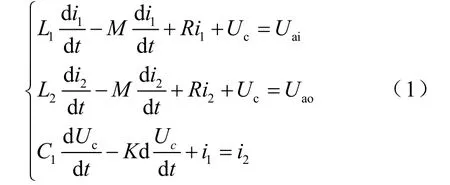
然后利用 Park公式變換，將式（1）轉換到兩相同步旋轉d，q坐標系，則

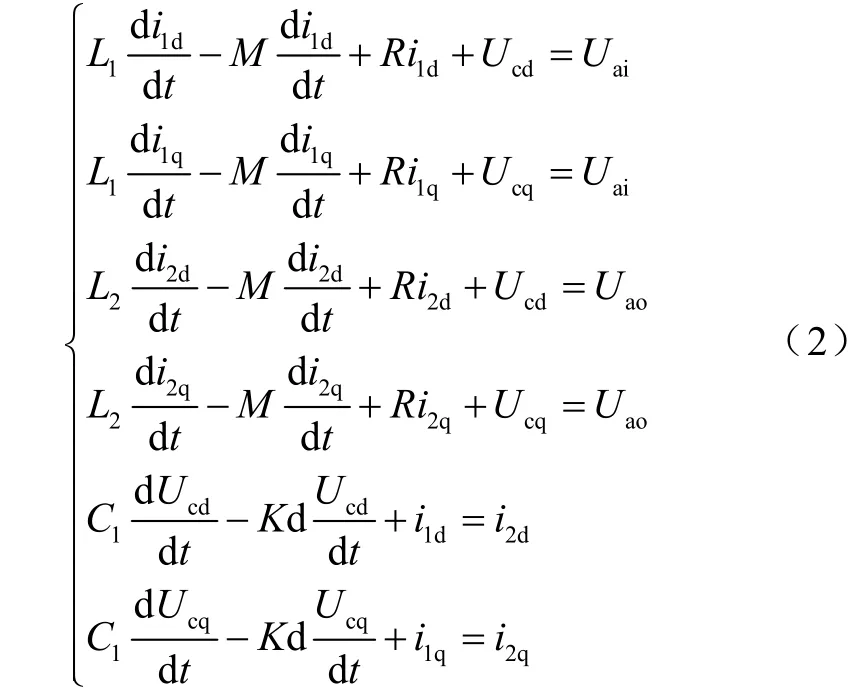
由式（2）可以得到數學模型如圖2所示，即LCL濾波器在d、q坐標系下的數學模型。

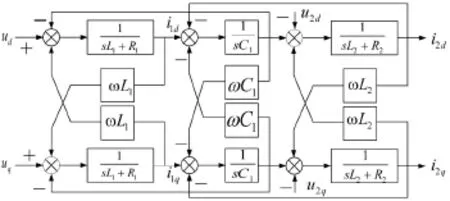
圖2 LCL控制器在坐標系下的數學模型

在圖2中，d、q軸電流除受控制量Ud、Uq影響外，還受耦合電壓和耦合電流的影響。如果引入狀態反饋對這些耦合量全部進行解耦控制，不僅引入的狀態量比較多，而且需進行復雜運算，這使控制相關的系統參數隨之增多，使得控制性能非常依賴建模時各個參數的精確度。而此類參數對系統影響作用不大，故忽略耦合參數，將上式簡化為

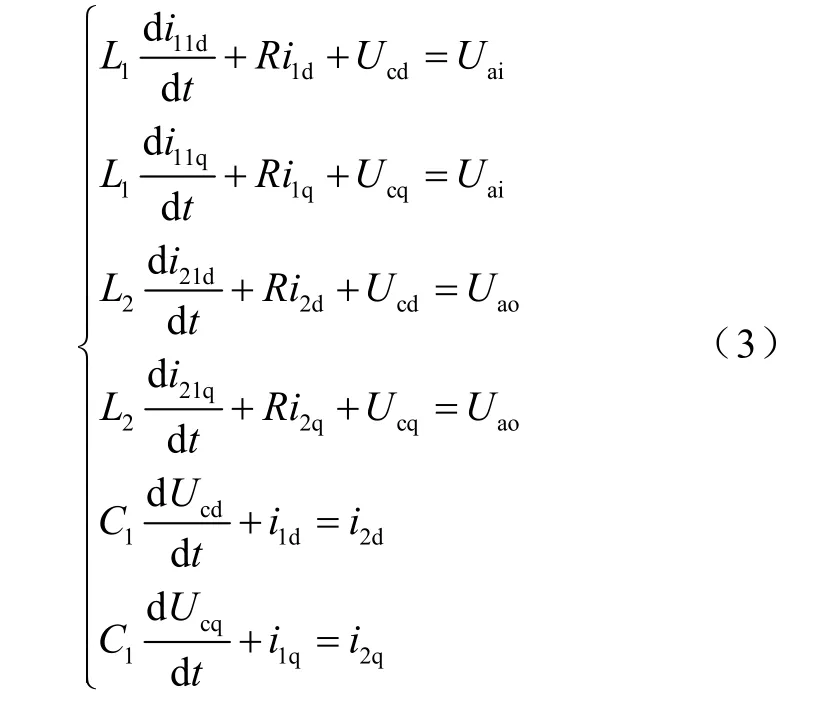
2 復合控制

系統輸出電能的質量以及其穩定性是整個光伏微網系統重要的技術指標。由于動態響應快、收斂性良好和原理簡單，近年來無差拍控制（deadbeat control）已被越來越多地應用在PWM逆變控制[11]。無差拍控制（deadbeat control）的基本思想是使系統在每一個采樣點上的輸出與其指令保持完全一致，不存在任何相位和幅度的偏差。無差拍控制系統中下一拍的輸出量總能表示成當前周期的輸入控制量和系統狀態變量的線性組合。因此新裝置的逆變器的狀態方程和輸入控制信號推算出下一個周期的輸出控制量，從而理論上可以使輸出電流在相位和幅值上都非常接近參考電流。從而，由負載變化或非線性負載引起的輸出電流誤差可在一個開關周期內得到校正。然而，單一的控制無法及時應對外界的干擾，往往不能得到高質量的電能輸出。PI控制具有良好的穩定性，且原理簡單，易于實現[12]。故本文提出一種電壓內環無差拍控制與電流外環PI控制相結合的復合控制，具體控制如圖3所示。

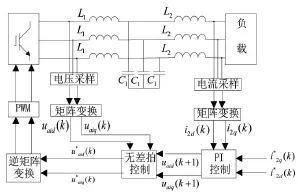
圖3 基于LCL濾波器的復合控制框圖

2.1 電壓內環無差拍控制

根據無差拍控制原理，對式（2）中的d軸和q軸進行解耦，分別得到解耦后的控制單元輸出指令的計算公式

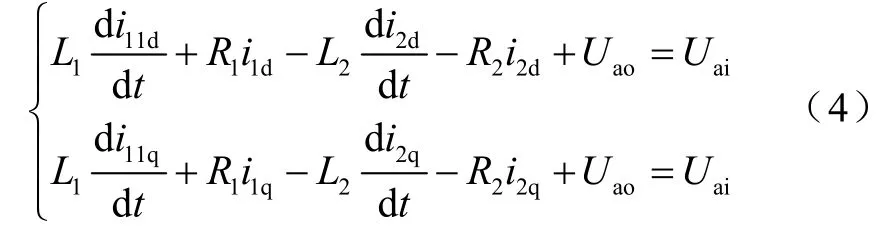
為了對指令電流進行無差拍控制，令采樣周期的占空比為T，將式（4）離散化，得PWM整流器離散化后的數學模型為

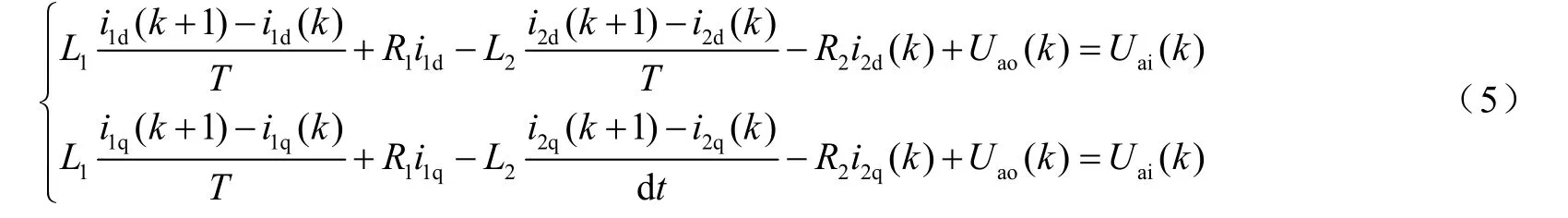
將（5）式整理得

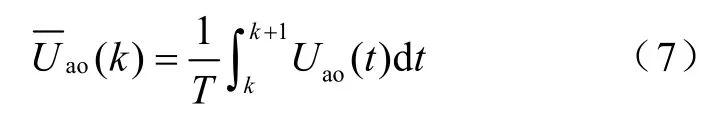
由無差拍控制可以得到PWM波形的電壓指令為

2.2 電流外環PI控制

由圖1可以得到濾波單元的簡化電路，如圖4所示。

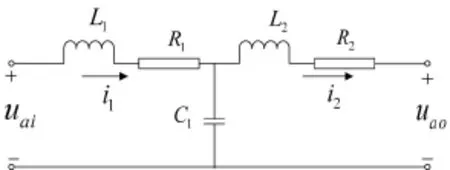
圖4 單相光伏發電系統簡化電路圖

可設（L2+ R2）與C1C1并聯阻抗為X，即

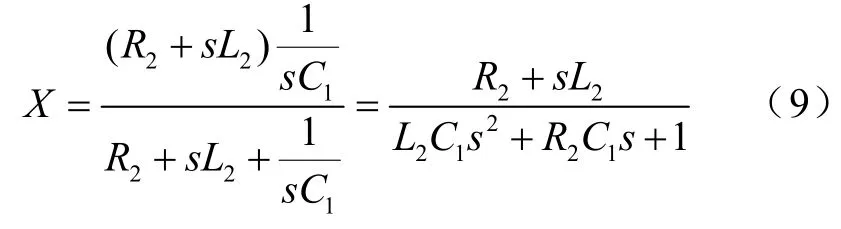
則從直流側可以求得從整流單元的總輸入阻抗為Xs，則

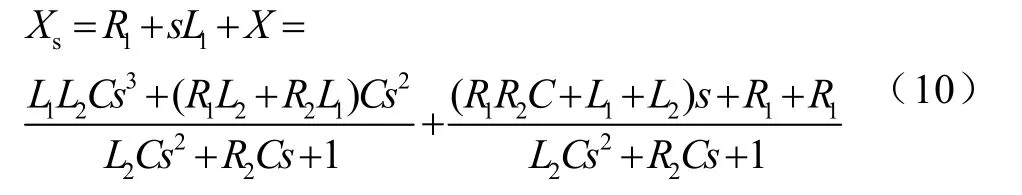
逆變器側電流為i1，則

電網側電流為i2，有

輸出電壓與電網側電流之間的傳遞函數為

設置的主要參數有：濾波電感L1為3.05mh；濾波電感L2為9.60mh；濾波電容C1為10μF；電阻 R1為 0.81Ω；電阻 R2為 2.56Ω。由式（10）可以得到LCL濾波單元的bode圖。

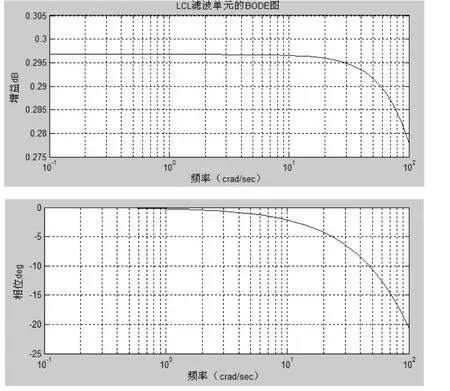
圖5 濾波單元i2-uai傳遞函數bode圖

由圖5顯而易知，在中低頻段增益為一個定值，在高頻段幅頻增益迅速衰減；且在中低頻段相位穩定在零度，具有良好的濾波效果和穩定性。

PI控制單元能對傳遞函數進行校正，提高濾除諧波的穩定性，則PI控制單元表示為

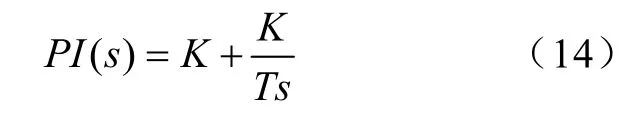
式（13）中，K為PI控制單元增益（K=0.25）。將電流環進行離散化，得到開環傳遞數為

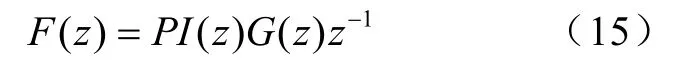
式（10）中， z-1為控制對象離散化后的傳遞函數，G( z)為PI控制單元離散化后的傳遞函數。故求得電流環的離散化閉環傳函數為

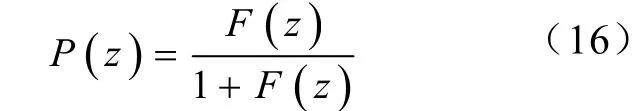
其中指令電流 i*2q(k)和i*2d(k)由DSP產生，將代入無差拍控制即能實現新型復合控制。在工頻電能周期內，存在各次諧波和閃變，無差拍控制能及時協調負載側電流不穩問題，PI控制能從整體上控制光伏系統的穩定運行。故本設計控制方案能濾除各次諧波，提高了光伏微網系統的穩定性，同時大大改善了電網和負載的電能質量。

3 實驗仿真

為了驗證上述理論的正確性，通過新系統結構和數學模型的詳細推導，可以利用Matlab/Simulink對新系統建立仿真模型。仿真結構模型令太陽發電直流側電壓為400V，負載為三相非線性負載。

圖6（a）是基于傳統的控制下得并網逆變器輸出的電流波形圖，圖6（b）是基于本文的控制方案的輸出電流波形圖；從圖 6、圖 7可以看出本文控制方案能濾除各次諧波。通過仿真顯而易得，傳統光伏發電的A相電流總諧波失真（THD）為7.22%，而本文提出的控制方案下得電流諧波總畸變率為4.61%，如圖6所示。

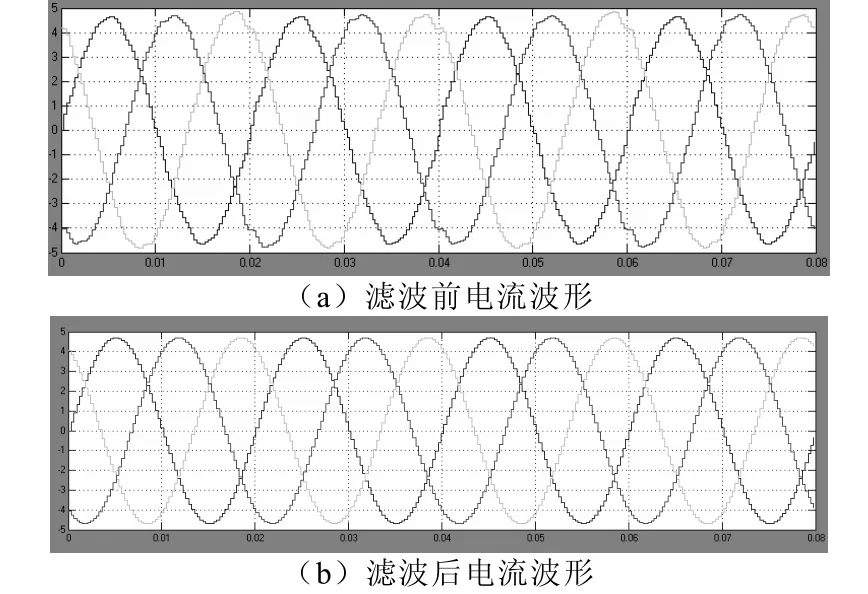
圖6 負載輸出側電流波形

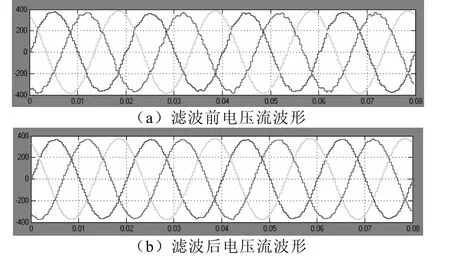
圖7 直流側電壓流波形

對上圖輸出電流進行頻譜分析，從圖中顯而易得，本文的控制方案更具濾除高次諧波的明顯優勢。

4 結論

綜上所述，在配電網中，本文提出的基于無差拍控制和PI控制相結合的控制策略既克服了APF成本高和功能單一的缺點，又能更有效地濾除三相光伏發電中的各次諧波，有效地降低了并網電流的波形畸變率，提高了電網的電能質量和系統的穩定性。

[1]KADRI R, JEAN-PAUL, GAUBERT, CHAMPENOIS G,MOSTEFAI M. Design of a single-phase grid-connected photovoltaic system based on deadbeat current control with LCL filter[C].IEEE Power Electronics and Motion Control Conference, 2010(14):147-153.

[2]王兆安,楊君,劉進軍.諧波抑制和無功功率補償[M].北京:機械工業出版社,1998.

[3]魏星,肖嵐,等.三相并網逆變器的LCL濾波器設計[J].電力電子技術.

[4]李練兵,趙志國,趙昭,等.基于復合控制算法的三相光伏并網逆變系統的研究[J].電力系統保護與控制,2010(11):44-47.

[5]張亮,蔡旭,等.并聯型有源電力濾波器設計及并網沖擊電流的抑制.[J]電機與控制學報,2010(3):39-44.

[6]劉飛,查曉明,等.基于極點配置與重復控制相結合的三相光伏微網系統的并網策略.[J].電工技術學報,2008(12):130-136.

[7]張輯,魏盛彪,孫祖明.SVPWM 整流器的無差拍控制技術[J].制造業自動化,2010(3):236-239.

[8]夏向陽,龔芬,周峰.配電網中分布式并網發電裝置的復合控制策略[J].高電壓技術2011,37(8):2010-2015.

[9]夏向陽,羅安.單獨注入式有源濾波器的整體優化設計[J].高電壓技術,2009,35(5):1137-1143.

[10]袁性忠,王婷,朱俊星.有源電力濾波器無差拍控制策略的研究[J].電力電子技術,2010(4):38-47.

[11]劉勝榮,楊蘋,肖瑩,等.兩級式光伏并網逆變器的無差拍控制算法研究[J].電力系統保護與控制, 2010(4):26-29.

[12]全曉明,申群太.基于 DSP無差拍控制的逆變電源研究[J].現代電子技術, 2009(9).