基于蟻群優化K-medoids的變電站特性聚類研究

劉建華 孟 穎 譚 智

（1.長沙理工大學電氣與信息工程學院，長沙 410114；2.長沙理工大學計算機與通信工程學院，長沙 410114）

眾多文獻研究表明負荷特性對于電力系統運行，特別是電力系統的動態行為有很大的影響[1]，電力負荷模型準確與否直接影響到電力系統仿真結果的準確性[2-3]。建立精確的負荷模型用于電力系統的規劃、設計、運行和研究越來越成為電力系統工程實際和學術研究的基本需要[4]。但是由于負荷自身的特殊性，建立精確的電力系統負荷模型非常困難。

隨著對負荷建模研究的逐漸深入，負荷特性的分類與綜合問題正在受到重視。電力系統負荷變化的規律性使負荷數據呈現出可分類的特點[5-6]。文獻[7]中提出了基于改進K均值(K-Means)的負荷聚類算法對電網進行仿真分析。文獻[8]中提出了模糊等價關系和模糊C均值(Fuzzy C Means，FCM)兩種負荷聚類方法。文獻[9]提出了基于自適應FCM聚類的電力負荷動特性分類方法。文獻[10]提出了基于數據挖掘的多層次細節分解負荷聚類算法。

本文提出了一種蟻群優化 K-medoids綜合算法（下文簡稱綜合算法），并將其應用于變電站負荷特性聚類中，通過K-medoids算法對蟻群的歷史最優位置進行聚類分析，將此位置代替K-medoids算法的參考點，作為新的聚類中心，數據可以自適應的加入到適合它的聚類當中。

1 基本原理

1.1 蟻群算法

蟻群算法是Colorni和Dorigo等人在90年代初期提出的一種新型智能模擬仿生優化算法[11]。蟻群算法由于具有正反饋、分布式計算以及貪婪啟發式搜索等特點，成為人工智能領域的一個研究熱點。目前對蟻群算法的研究已經滲入到多種不同的應用領域，如旅行商問題（TSP）、二次分配問題（QAP）、任務調度問題（JSP）等。

蟻群算法的基本原理是[12]，螞蟻在運動過程中會釋放一種信息素（pheromone）的物質，螞蟻個體之間是通過該信息素進行運動方向的信息傳遞的，即螞蟻不僅在所經過的路徑上沉積了該種物質，而且螞蟻在運動過程中能夠感知這種信息素物質。因此，由大量螞蟻組成的蟻群行為便表現出一種信息正反饋和相互協作的機理：某一路徑上走過的螞蟻越多，則后來者選擇該路徑的概率就越大，即運用群體信息素來作為引導它們運動軌跡方向的依據，最后螞蟻能找到一條從蟻巢到食物源的最短路經，這就是整個群體得以完成復雜優化行為的實質問題。即使遇到障礙物情況，該基本原理仍然是不變的，只不過是在運動的途徑上會增加沉積信息素的中間狀態點來解決，信息交換構成一個正反饋過程仍是不變的。

1.2 K-medoids算法

K-medoids聚類算法[13]的基本策略是通過首先任意為每個聚類找到一個代表對象而首先確定n個數據對象的k個聚類；其他對象則根據它們與這些聚類代表的距離分別將它們歸屬到各相應聚類中。而如果替換一個聚類代表能夠改善所獲聚類質量的話，那么就可以用一個新對象替換舊聚類對象。這里將利用一個基于各對象與其聚類代表間距離的成本函數來對聚類質量進行評估。為了判定一個非代表對象Orandom是否是當前一個代表對象Oj的好的替代，對于每一個非中心點對象p，下面的4種情況被考慮。

第一種：p當前隸屬于中心點對象Oj。如果Oj被Orandom所代替作為中心點，且p離一個Oj最近，i≠j，那么p被中心分配給Oi。

第二種：p當前隸屬于中心點對象Oj。如果Oj被Orandom代替作為一個中心點，且p離Orandom最近，那么p被重新分配給Orandom。

第三種：p當前隸屬于中心點Oi，i≠j。如果Oj被Orandom代替作為一個中心點，而p仍然離Oj最近，那么對象的隸屬不發生變化。

第四種：p當前隸屬于中心點Oi，i≠j。如果Oj被Orandom代替作為一個中心點，且p離Orandom最近，那么p被重新分配給Orandom。

每當重新歸類時，平方誤差E所產生的差別對成本函數有影響。因此，如果一個當前的中心點對象被非中心點對象所代替，成本函數計算平方-誤差值所產生的差別。替換的總成本是所有非中心點對象所產生的成本之和。如果總成本是負的，那么實際的平方誤差將會減小，Oj可以被Orandom替代。如果總成本是正的，則當前的中心點Oj被認為是可接受的，在本次迭代就無需變動。

2 蟻群優化K-medoids綜合算法

2.1 基本思想

綜合算法的基本思想：從蟻群中隨機選取m個對象，計算任意兩個對象之間的距離，確定蟻群間的距離和最初的聚類中心，并將此中心作為蟻群的歷史最優位置，使用K-medoids算法對歷史最優位置進行聚類分析，找到新的聚類中心，來代替蟻群算法逼近優化的中心點。首先，螞蟻之間在利用螞蟻釋放的信息素，確定蟻群在可行解范圍內的相對位置，實現螞蟻之間的信息交換；其次，根據螞蟻所在蟻群中心提供的信息素，擴大螞蟻的搜索空間，從而避免螞蟻陷入局部最優，加強算法對聚類所在空間區域的局部搜索能力；最后，從整個蟻群的角度出發，由于每只螞蟻的搜索范圍都集中于新的聚類所形成的區域，重新計算任意螞蟻之間的距離，確定最終的聚類中心。

2.2 實現過程

1）流程圖（如圖1）

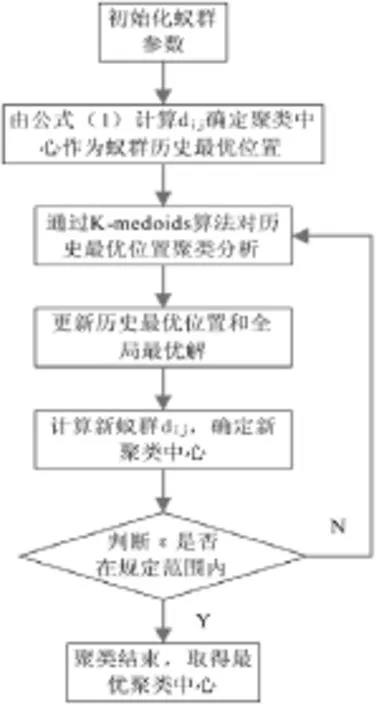
圖1 綜合算法流程圖

2）實現步驟

設 X={Xi=(xi1，xi2，…，xim)，i=1，2，…，N}是待進行聚類分析的數據樣本的集合。

Step1 對蟻群進行初始化操作，選擇螞蟻數目為m，NC-max為最大迭代次數，m個螞蟻作為初始中心點，設初始中心點為（M1，M2，…，Mm）。

Step2 定義dij為Xi到Xj之間的加權歐氏距離

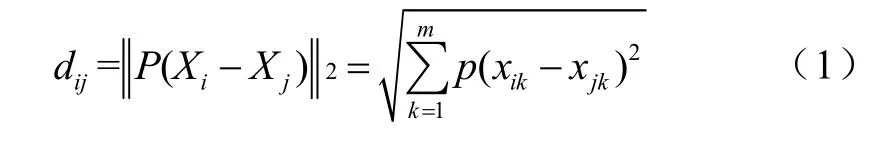
式中，P為權因子，可根據各分量在聚類中的貢獻不同而設定。

設r為聚類半徑，τ ij ( t)為t時刻數據樣本Xi到樣本Xj路徑上殘留的信息數量（Pheromone Quantity，PQ）PQ，設 τ ij ( 0)=0，即在初始時刻各路徑上的PQ相等且為0。路徑ij上PQ由式（2）給出

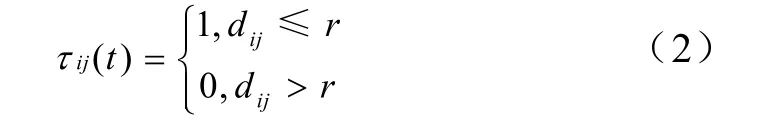
而Xi是否歸并到Xj由式（3）給出

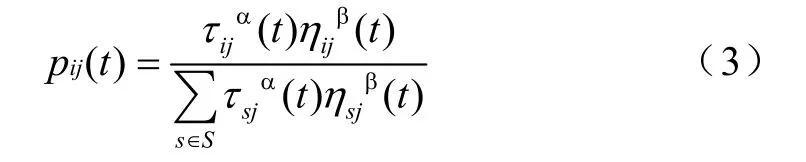
式中， p ij ( t)表示Xi歸并到Xj的概率，若 p ij( t)≥p0，（0≤p0≤1），則Xi歸并到Xj領域。其中，p0為一概率常數。S={Xs|dsj≤r，s=1，2，…，j，j+1，…，N}；η為局部的啟發函數，表示由數據樣本i轉移到數據樣本j的期望程度。α，β分別表示螞蟻在運動過程中所積累的信息素及啟發函數在樣本轉移路徑的過程中所起的不同作用。

根據加權歐氏距離式（1），計算每只螞蟻之間的距離dij，然后由式（3）計算 p ij( t)判斷PQ，確定蟻群間的最優路徑和聚類中心，并將此中心作為蟻群的歷史最優位置。

Step3 根據K-medoids算法對蟻群的歷史最優位置進行新的聚類分析。以ACO算法的歷史最優位置作為K-medoids算法中的代表對象Oj，確定每只螞蟻所在的聚類以及類與類之間的中心點。

Step4 對形成的新蟻群按照Step2的方法，計算每只螞蟻代表的最優解，更新蟻群的歷史最優位置和全局最優解。

Step5 重新計算任意螞蟻之間的加權歐氏距離dij，確定新的聚類中心，找到最優路徑。

Step6 定義Dj為第j個聚類的偏離誤差，ε為聚類分析的總體誤差。

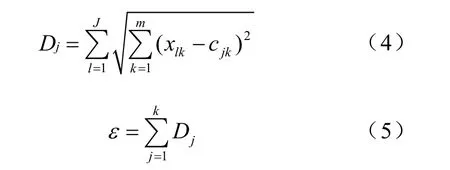
式中，cjk為第j個聚類中心的第k個分量。

判斷ε是否在規定范圍內，如在規定范圍內，聚類終止，否則轉向Step3繼續迭代。

Step7 達到終止條件，聚類結束，取得最優聚類中心。

3 聚類實例

3.1 聚類數據

取文獻[14]中福建省電力調度通信中心EMS提供的2005年夏季的典型電網變電站負荷構成數據進行聚類分析。矩陣U為變電站負荷構成參數，待分對象：U={u1，u2，u3，…，u44}為44個220kV變電站負荷構成參數；列對象參數：ui={uil，ui2，ui3，ui4}為各變電站的工業、農業、商業、城鄉居民及其他4類典型行業負荷的構成比例。本文把變電站聚為4類。

3.2 聚類結果

如表1和表2所示，將綜合算法與單一的FCM的聚類結果進行比較，以驗證其聚類的效果。同時列出兩種方法的聚類中心矩陣CFCM和C綜合。

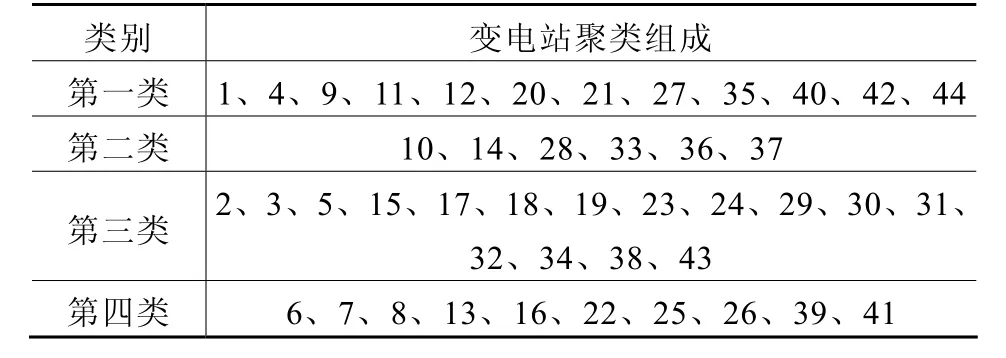
表1 FCM法的聚類結果

聚類中心矩陣為

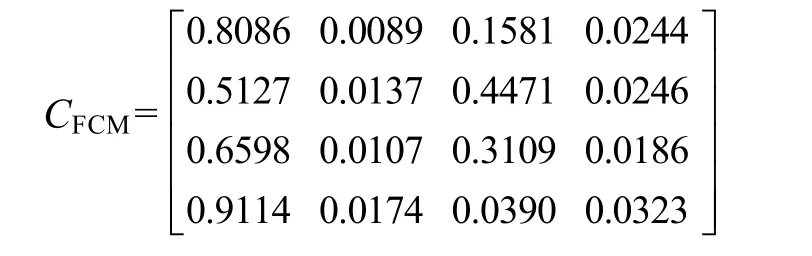
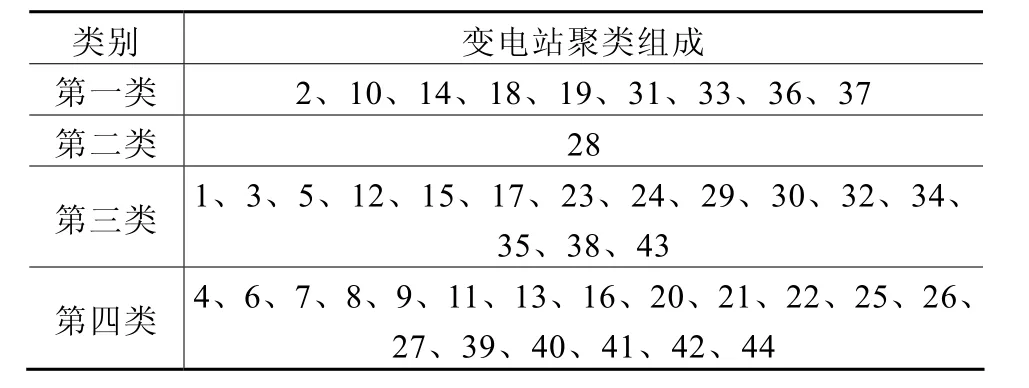
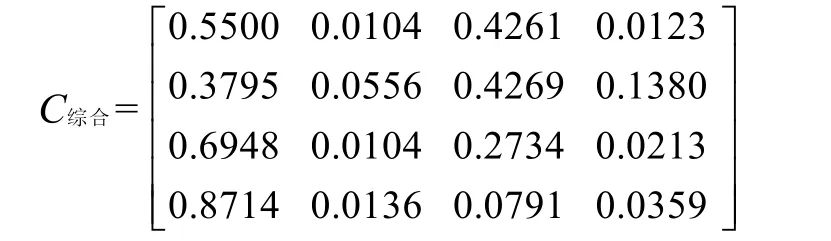
表2 綜合算法的聚類結果

聚類中心矩陣為

3.3 類間距離和類內距離比較

聚類結果的好壞要看是否有較高的類內相似性，較低的類間相似性。本文可以對它們的類間距離和類內距離進行比較，一般來講，聚類中心的間距越大，樣本與其所屬中心的間距越小，聚類效果更好。因此，我們只列出它們的類間距離和類內距離進行比較。

1）類間距離：由聚類中心矩陣可以求得類間距離矩陣，取矩陣中的每個元素的平均值作比較，較大者則認為聚類效果比較好，反之亦然。如表3所示。

表3 類間平均距離比較

2）類內距離：類內平均距離比較如表4所示。

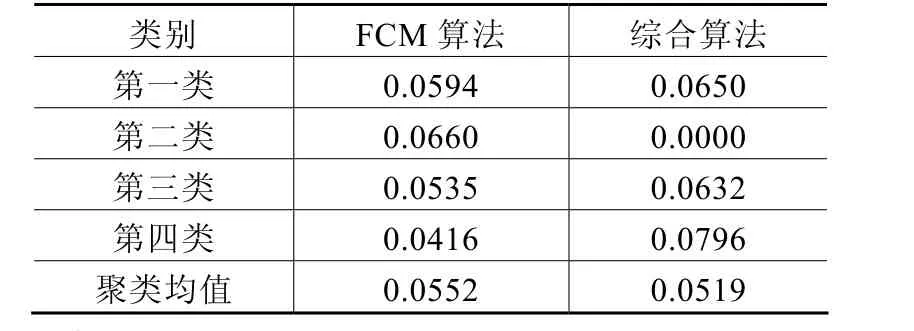
表4 類內平均距離比較

3.4 結果分析

1）如表3和表4所示，綜合算法的類間距離有所變大，類內距離有所變小，可知綜合算法在變電站的聚類中取得了較好的效果。

2）對聚類中心矩陣與變電站負荷構成數據進行比較，基于綜合算法的聚類結果是有效和合理的。例如第一類，工業用電約占55%，商業用電約占43%，農業和城鄉居民及其他各約占1%，基本上反映了第一類各變電站的綜合靜態負荷特性構成。聚類中心矩陣中可以較好地體現出每類變電站的綜合靜態負荷特性。

3）由聚類結果和中心矩陣可得出安裝負荷測辨裝置的變電站數量和具體位置，即負荷裝置布測點的個數為聚類數，理想的安裝測點是與聚類中心負荷構成特性最為接近的典型變電站。

4 結論

負荷特性分類與綜合是實現負荷模型實用化的關鍵，為了建立合適的變電站負荷模型，本文將聚類方法引入到負荷特性分析，提出了基于蟻群優化K-medoids綜合算法的電力負荷聚類。綜合算法是PAM算法對蟻群的歷史最優位置進行了聚類分析，ACO具有良好的正反饋性能、較強的魯棒性、易于與其他算法結合等特點，使綜合算法能更好地獲得全局最優解，從而克服了PAM算法易陷入局部最優的缺點，并降低了對初始值的敏感度，提高了聚類的準確率。通過變電站特性聚類實例，將綜合算法與FCM法聚類結果進行比較，證明了綜合算法在電力系統負荷聚類的優越性。同時基于綜合算法的負荷聚類為沒有安裝布測點的變電站建立實用模型提供了有效途徑，因此，文中所得到的聚類結果和聚類中心矩陣為進一步開展負荷建模實用化工作提供了重要的參考依據。

[1]李娟,丁堅勇.電力系統負荷建模和算法的研究及進展[J].高電壓技術,2008,34(10):2209-2215.

[2]李培強,李欣然,林舜江.電力負荷建模研究評述[J].電力系統及其自動化學報,2008,20(5):57-64.

[3]鞠平,謝會玲,陳謙.電力負荷建模的發展趨勢[J].電力系統自動化,2007,31(2):1-4.

[4]賀仁睦.電力系統精確仿真與負荷模型實用化[J].電力系統自動化,2004, 28(16):4-7.

[5]章健,沈峰,賀仁睦.電力負荷模型結構的樣條函數描述[J].電力自動化設備,2007,27(7):5-8.

[6]黃梅,賀仁睦,楊少兵.模糊聚類在負荷實測建模中的應用[J].電網技術,2006,30(14):49-52.

[7]白雪峰, 蔣國棟.基于改進 K-means聚類算法的負荷建模及應用[J].電力自動化設備,2010,30(7):80-83.

[8]李培強, 李欣然,陳輝華,等.基于模糊聚類的負電力負荷特性的分類與綜合[J].中國電機工程學報,2005, 25(24):73-78.

[9]楊浩,張磊,何潛,等.基于自適應模糊C均值算法的電力負荷分類研究[J].電力系統保護與控制,2010,38(16): 111-115.

[10]張智晟,孫雅明,張世英,等.基于數據挖掘多層次細節分解的負荷序列聚類分析[J].電網技術,2006,30(2):51-56.

[11]周申培,嚴新平.遺傳蟻群融合算法及在不確定性無功優化中的應用研究[J].電力系統保護與控制,2010,38(24):120-123.

[12]孫雅明,王晨力,張智晟,等.基于蟻群優化算法的電力系統負荷序列的聚類分析[J].中國電機工程學報,2005,25(18):40-45.

[13]朱明.數據挖掘[M].合肥:中國科技大學出版社,2008.11.

[14]鞠平, 陳謙, 熊傳平,等.基于日負荷曲線的負荷分類和綜合建模[J].電力系統自動化, 2006, 30(16):6-9.