基于量子粒子群算法的電力系統無功優化

張 斌 劉 幸

（1.陜西省地方電力（集團）有限公司延安分公司，陜西 延安 716000；2.華北電力大學，北京 102206）

電力系統無功優化主要是指在不同的條件下，充分使用各種控制手段，來有效達到降低系統功耗，提升電壓水平的方法。在數學上，必須使用多目標、多約束、非線性、非連續、混合整數組合，才能達到優化的目的。因為，在計算過程中，需運用到多個連續變量，也需要運用到多個離散變量，使得優化過程十分復雜。

一般而言，常用的優化方法有如下幾種：線性規劃、非線性規劃、二次規劃、混合整數法等，每種方法都有其各自的特點和優越性，但缺點也是非常明顯的，它們只能對與初始點有關的局部最優解進行搜索，同時，對目標函數和約束條件有連續、可微的要求，耗費時間長，并且時常有“維數災”的情況發生。與此同時，科技的不斷發展和進步，各種先進算法已經成功應用到電力系統的無功優化問題上來，通過多年的實踐，已經取得了不錯的效果。如粒子群算法、量子算法等。

粒子群優化算法（PSO）[1]是在 1995年由Eberhard和Kennedy等人首先提出，它是一種基于種群搜索的自適應進化計算技術，由于其概念和參數調整簡單并容易編程實現，得到了廣泛應用，但是PSO算法的早熟收斂問題一直無法破解，因此其應用性受到了一定的限制。

量子計算[2-3]在20世紀90年代中期得到廣泛應用，它的最大的優點在于其具有強大計算能力，不少研究者將經典算法和量子算法結合起來進行研究，實現了性能上的突破，如Han提出的量子遺傳算法，Sun提出的基于量子行為的粒子群優化算法等。疊加態特性和概率表達特性是量子進化算法的兩大特點，疊加態特性最大的特點在于讓單個粒子呈現出多種不同的狀態，具有種群多樣性；概率表達特性幫助粒子以一定概率跳出局部最優解。但是，量子進化算法的編碼采用二進制編碼，對于數值優化問題由于需要頻繁編碼解碼，加大了計算量；更新策略一般通過既定的查詢表實現，沒有充分利用進化過程中粒子的協同性。

本文應用的量子粒子群算法[4]基于實數編碼，并且融入PSO的更新策略，不僅保持了種群多樣性而且大大增加了搜索效率。而且，本文的算法提供了一種量子包容機制，可以包容各種改進的PSO算法。IEEE-30電力系統無功優化測試算例證明了算法的高效性和魯棒性。

1 數學模型

本文選用網絡損耗最小為目標函數[5]，控制變量分別為發電機機端電壓、變壓器分接頭位置、并聯電容器的投切組數。等式約束包括有功功率以及無功功率的平衡，不等式約束包括節點電壓約束，發電機無功約束，電容器無功容量約束等。通過功率流動計算可以自動滿足等式約束，同時采用罰函數的方法處理控制變量的上下界，滿足不等式約束。

1.1 原始目標函數

無功優化問題描述如下：

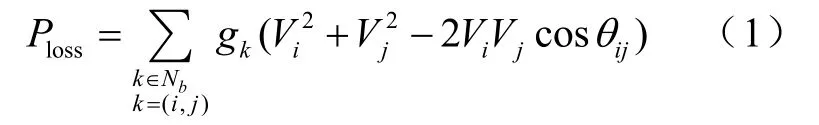
1.2 約束條件

潮流約束

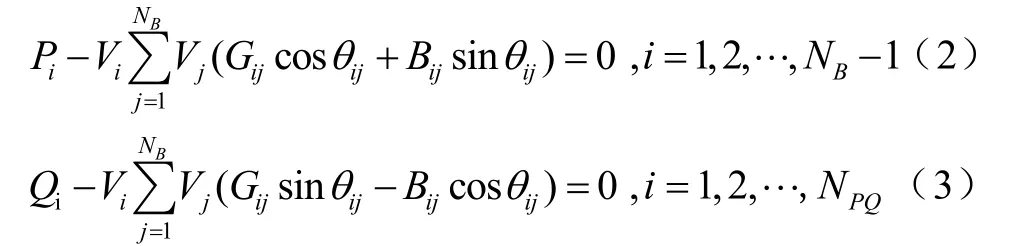
電壓約束

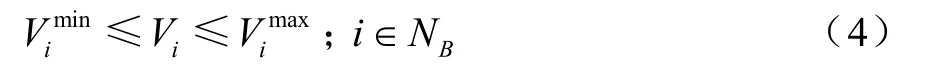
發電機無功約束

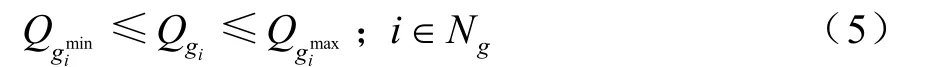
電容器無功約束

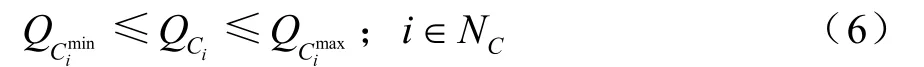
變壓器分接頭設定約束

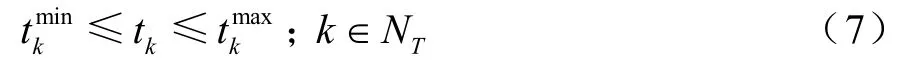
線路容量約束

其中，Ploss為系統有功損耗；Pi，Qi分別表示節點i的注入有功功率和無功功率；Gij，Bij分別表示節點i和節點j之間的電導和電納；Qgi表示節點i接入的無功發電機；Qci表示節點i出補償電容器的出力；tk表示支路k上變壓器分接頭的位置；Vi，Vj分別表示節點i和節點j的電壓水平；θij表示節點i和節點j的電壓相量角；Sl表示通過第l條支路的視在功率；gk表示支路 k的電導；NB表示節點總數；NB-1表示除平衡節點以外的節點總數；NPQ表示 PQ節點總數；Ng表示發電機節點總數；Nc表示補償電容器投切組數；Nb表示系統支路數；Nt表示包含有載調壓變壓器的支路總數。

1.3 綜合目標函數

綜合考慮目標函數和約束條件，引入罰函數處理方法構造目標函數，如下式所示：

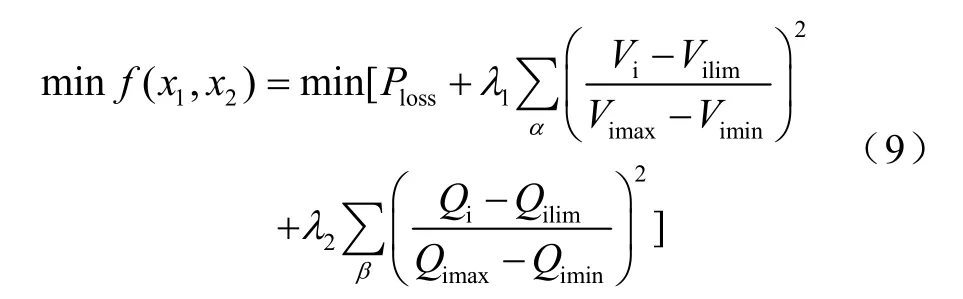
在上面的函數中，Vimax、Vimin為節點電壓Vi的上限和下限；Vilim、Qilim為i節點電壓和無功的限值；Qimax、Qimin為發電機節點無功出力 Qi的上限和下限；α、β分別為違反節點電壓約束和違反發電機無功出力約束的節點集合；λ1，λ2為違反電壓約束和發電機無功出力約束的懲罰因子。

2 量子粒子群算法

2.1 粒子編碼

粒子中的每一位采用量子比特的方式表示，就叫量子位。量子位的狀態除了|0＞和|1＞外，還可以是|0＞、|1＞的線性組合，通常稱其為疊加態，表示為|φ＞=α|0＞+β|1＞。其中，α 和 β是一對復數，稱為量子態的概率幅。量子態|φ＞因測量或者以|α|^2的概率坍縮到 0，或者以|β|^2的概率坍縮到 1，且滿足歸一化條件：|α|^2+|β|^2=1。因此，一個量子位可由其概率幅定義為[α, β]T，同理，m個量子位可定義成[αm, βm]T。

本文基于實數編碼，直接采用量子位的概率幅作為問題解，采用雙鏈編碼方案，如下所示

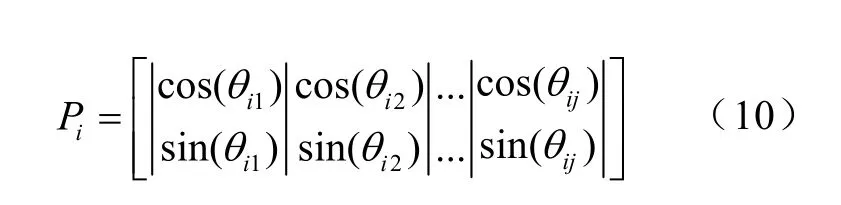
式中，θij=2π×rand；rand為（0,1）之間隨機數；i=1,2,…, m, j=1, 2, …, n；n是種群規模，m是空間維數。由此可見，種群中每個粒子占據解空間中兩個位置，分別稱為正弦位置和余弦位置。

2.2 解空間變換

不同于傳統的量子進化算法，本文直接使用粒子坍塌成某一基本態的概率參與適應度評價。由于粒子的每一維位置向量取值范圍不同，因此在計算適應度之前需要對粒子的位置向量進行解空間變換，如式（11）所示。

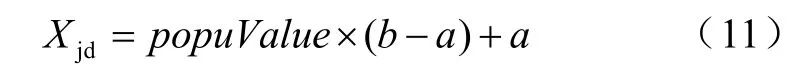
式中，popuValue為某基本態的概率；a，b分別為第j個粒子第d維的下界與上界；Xjd為第j個粒子第 d維由單位空間[-1,1]n映射到優化問題解空間的值。

2.3 粒子更新

本文為了突出量子概念的優越性，使用基本粒子群算法更新方式。更新策略如式（12）所示。

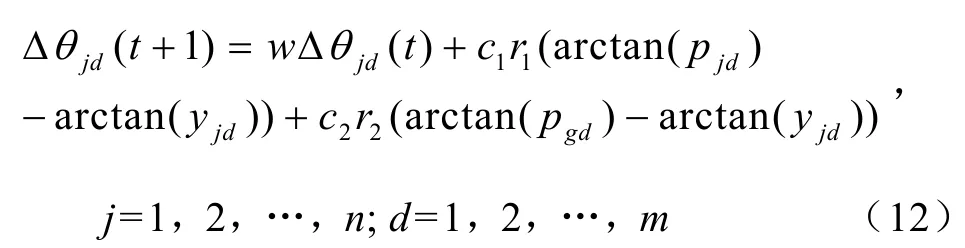
式中，w為慣性權重，Δθjd（t）為在第t次迭代中第j個粒子第d維的相移量，c1，c2是加速常數，r1，r2是均勻分布的隨機數，arctan（pjd）是第j個粒子歷史最優值第d維的相位，arctan（yjd）是第j個粒子當前第 d維的相位，arctan（pgd）是全局最優粒子第d維的相位。

根據得到的相移量，計算出量子旋轉門，然后更新粒子

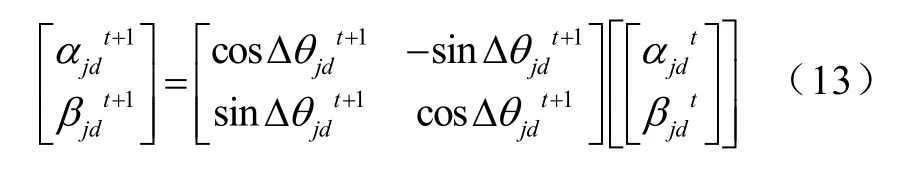
式中，Δθjdt+1為在第 t+1次迭代中第 j個粒子第 d維的相移量，αjdt, βjdt為在第 t次迭代中第 j個粒子第 d維的概率幅，αjdt， βjdt為第 t+1次迭代中第 j個粒子第d維的概率幅。

2.4 算法流程圖

量子粒子群算法的流程圖如圖1所示。

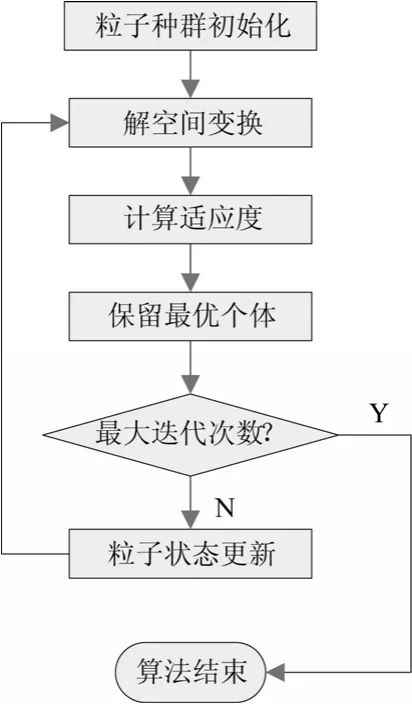
圖1 算法流程圖

3 基于量子粒子群算法的無功優化

用量子粒子群算法求解無功優化問題時，先對決策變量（發電機機端電壓、變壓器分接頭和無功補償量）進行量子染色體的編碼及種群的初始化，再通過解空間變換，實現量子染色體與決策變量的對應，然后調用潮流計算程序進行目標函數的計算及適應度的評價，保存個體最優信息和全局最優信息，更新量子門，實現種群的進化。

3.1 初始種群的產生

在電力系統無功優化中，各種變量的取值需非常謹慎，萬一出現差錯，對系統的影響是非常大的。這一點在控制變量上顯得尤為突出，在尋找最優解的實踐中，筆者發現，很多控制變量取值代表的運行方式對無功優化是毫無用處的。因此，本文采用傾斜分布方式產生初始解群[6]。

第一步，需根據下列三種類型判斷初始點的取值范圍，本文使用初始粒子種群進行潮流計算。

1）較多節點電壓越上限，系統是無功大量過剩狀態，需投入感性無功補償設備、降低發電機的機端電壓或切除容性無功補償設備。

2）較多節點電壓越下限，系統是嚴重缺無功狀態，需提高發電機機端電壓或投入容性無功補償設備。

3）少量節點電壓越下限或越上限，其余各節點電壓穩定，此時處于無功基本平衡。

原則是，分布節點時需在略高于當前值的范圍內。

3.2 狀態變量的處理

發電機機端電壓：按連續量處理，初始運行值在電壓指定的上下邊界的范圍內隨機初始化。優化過程中，其值在邊界范圍內更新；有載變壓器和電容器：按離散變量處理，初始運行值在規定的上下限中隨機產生。在優化過程中，通過映射編碼和取整的方法對離散變量進行處理。對于一個變比調節范圍在[Tjmin，Tjmax]之間，共有l個單位分接頭的變壓器，調節步長為Tstep=（Tjmax-Tjmin）/（l-1），假設第j維控制變量X[j]，則令X[j]的取值范圍等于分接頭的檔數，即1≤X[j]≤l。按照Tj=Tjmin+[X[j]-1]Tstep將 X[j]轉化為相應的變比值代入目標函數進行計算，其中[.]表示取整。電容器投切組數也按此方法處理。

3.3 電力系統無功優化步驟

本系統優化算法采用基于量子粒子群算法，其主要步驟如下：

1）首先對控制變量的維數及其范圍進行設置。設置量子粒子群算法的種群數量 popScale、最大迭代代數iterMax、慣性權重w、自身因子c1、全局因子c2。

2）進行初始潮流計算，根據無功優化的本質按照傾斜分布方式產生原始粒子種群，并設定當前進化代數iter=1。

3）概率幅的初始化。

4）根據式（11）進行解空間變換，然后計算種群適應度。若粒子目前位置優于自身記憶的最優位置，則用目前位置替換；若目前全局最優位置優于已記錄的全局最優位置，則用目前全局最優位置替換。

5）根據式（12）對粒子狀態更新。

6）判斷是否達到最大迭代次數。若是，程序結束。若否，返回第4步。

4 算例

本文采用IEEE-30節點標準系統測試量子粒子群算法的優化結果。首先判斷算法是否能執行，分別與傳統量子進化算法（QEA）、標準粒子群（PSO）分別比較，編程使用Matlab7.0。

IEEE-30節點具有11個控制變量，包含兩個并聯電容器節點、6臺發電機和4臺有載調壓變壓器。其中變壓器上下界分別取1.1和0.9，電容器上下界分別取 0.4和 0。系統負荷 Sload=284.3+j126.2，初始網損為8.324MW。節點和支路數據參見文獻[7]。

算法初始參數的設置[8]：種群大小為10；最大迭代次數100代；根據經驗加速常數c1和c2取2；慣性權重系數w采用根據迭代次數依次遞減的自適應調整法，公式如下：

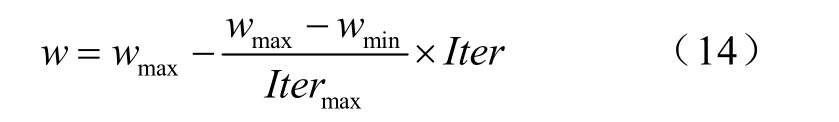
本文采用傾斜分布式啟發初始種群產生，因此需要在優化之前了解初始電壓情況。

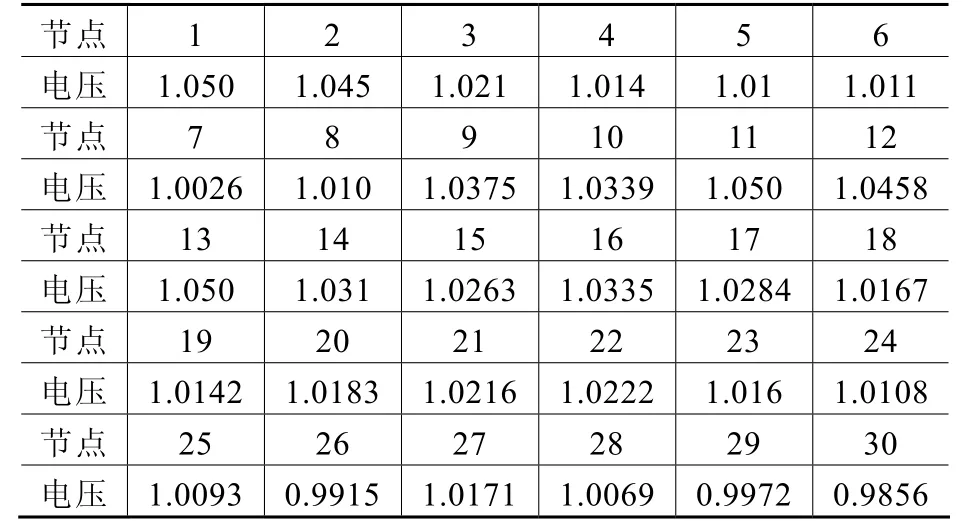
表1 IEEE-30節點初始潮流電壓情況

表1為初始潮流的電壓情況，優化前有功損失為8.324MW。由表1可以看出，所有節點的電壓合格，系統無功基本平衡。如果發電機機端電壓初始值為 1.00，將電壓劃分為 a-e五個區域：a為[1.06,1.10]，b 為[1.02,1.06]，c 為[0.98,1.02]，d 為[0.94,0.98]，e為[0.90，0.94]。機端電壓初始化為:a區域0%，b區域30%，c區域40%，d區域30%，e區域0%；并聯電容器容量設置為0；變壓器分接頭位置在控制范圍內隨機產生。

優化前后電壓曲線的對比圖如圖2所示。

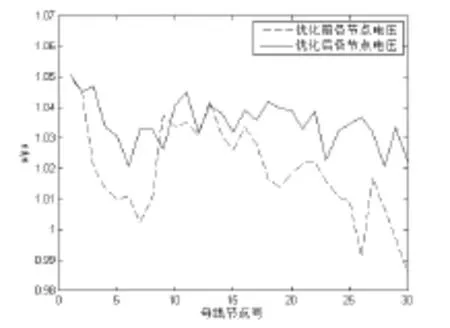
圖2 優化前后電壓曲線對比圖

優化前各節點電壓在取值范圍內，但是優化以后的電壓更加平穩。

分別采用 QPSO、PSO、QEA對電力系統無功優化的結果如表2所示。

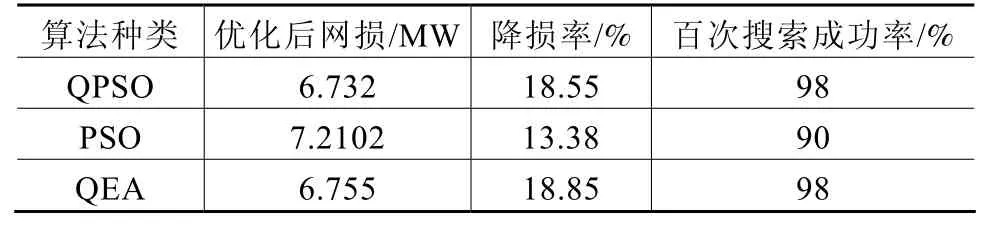
表2 QPSO，PSO，QEA結果對比表

由表2分析得知：①采用QPSO進行無功優化后，系統的有功損失為6.732MW，比優化前降低了18.55%，降損效果最為明顯。對算法各自測試 100次，其中QPSO和QEA的搜索成功率達到了98%，而PSO成功率只有90%，容易陷入局部最優解；②另外，從表中可以清楚看出，QPSO和QEA的尋優結果明顯優于PSO，證明了復雜問題中引入量子概念可以大大改善進化算法，其并行性和概率性既保證了搜索的效率又保證了種群多樣性。

圖3為QPSO、PSO、QEA在優化過程中粒子分布對比圖。

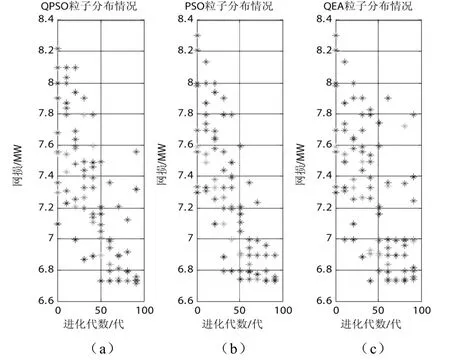
圖3 QPSO、PSO、QEA粒子分布對比圖

該圖是在100次測試中隨機選取的一次，對結果分析如下：

1）QPSO既能實現量子算法的并行性搜索，又能考慮到迭代過程中種群全局最優解和自身最優解對尋優的引導性以及粒子之間的協同性，因此尋優速度很快，由圖 3（a）可以看出算法在 50代附近已經找到了最優解6.732MW。量子理論還有一個特點是概率性，能保證搜索中種群的多樣性，即使搜索后期，仍有粒子分布在離最優解較遠位置，防止陷入局部最優。

2）PSO的更新策略是通過記錄每次更新后的全局最優值和粒子自身最優值，依賴粒子間信息互動尋求最優解，收斂速度與種群規模相關，一般解決復雜問題需要30～200粒子共同尋優。另外，從圖3（b）可以看出，粒子在尋優后期聚集在一起，容易陷入局部最優。

3）圖3（c）是傳統QEA尋優的粒子分布圖。由圖可以看出進化過程中粒子分布隨機，但是收斂速度很快，在50代附近尋到了最優值。QEA的更新策略是采用查詢表的方式[9]，比較呆板且無法利用環境信息導致尋優的盲目性。

5 結論

本文采用一種量子粒子群算法解決無功優化問題，結合量子進化算法的疊加態特性和概率表達特性，以及粒子群算法的粒子協同性等優點，算法尋優速度快，魯棒性強。采用傾斜式啟發種群初始化，減少了不可行解的數目，提高了算法效率。通過對IEEE-30典型測試系統的計算分析表明，本文提出的量子粒子群算法在求解大規模電力系統無功優化問題上具有快速、高效、準確的優點，可以嘗試用于其他的復雜電力系統優化。

[1]劉建華.粒子群算法的基本理論及其改進研究[D].湖南:中南大學,2009.

[2]李世勇,李盼池.量子計算與量子優化算法[D].哈爾濱:哈爾濱工業大學,2009.

[3]李世勇,李盼池.量子搜索及量子智能優化研究進展[J]. 計算機測量與控制,2009, 17(7).

[4]呂強,陳如清,俞金壽.量子連續粒子群優化算法及其應用[J].系統工程理論與實踐,2008,5(5):122-130.

[5]李秀卿,孫守剛,姜世金,許傳偉.基于混合優化微分進化算法的電力系統無功優化[J].電力系統保護與控制,2009,37(7):26-29.

[6]張炳才,秦四娟,喬世軍,盧志剛.基于改進微分進化算法的電力系統無功優化[J].電力系統保護與控制,2010,38(15):91-94.

[7]靳曉凌,趙建國.基于改進二進制粒子群優化算法的負荷均衡化配電網重構[J].電網技術,2005,29(23):40-43.

[8]周文.粒子群優化算法及其參數設置的研究[J].湖北職業技術學院學報.2006,9(4):93-96.

[9]Hong-mei Ni, Wei-gang Wang. A Niche Quantum Genetic Algorithm Used in Multi-peak Function Optimization [A]. Sixth International Conference on Natural Computation, 2010.