拉索高強鍍鋅平行鋼絲摩擦系數的進一步確定
陳 璨,鄭 罡,燕海蛟,杜 淵
(1.重慶交通大學土木建筑學院,重慶400074;2.招商局重慶交通科研設計院有限公司,重慶400067)
平行鋼絲斜拉索的局部彎曲應力的大小直接與彎曲剛度的大小取值、鋼絲間是否發生滑移相關。斜拉索是否發生滑移主要取決于索體內部鋼絲之間的極限摩擦剪應力與斜拉索鋼絲間受到的剪應力的大小。因此,準確測定斜拉索高強鍍鋅平行鋼絲摩擦系數值非常重要。
對斜拉索鋼絲摩擦系數值的初步研究表明,在自重作用下和小荷載作用下,斜拉索內平行鋼絲間摩擦系數均值為0.210 8[1],但該研究所施加的正壓力值過小,無法達到實橋中拉索所受正壓力值的大小。故筆者對斜拉索內高強鍍鋅平行鋼絲摩擦系數進行了進一步的確定。影響摩擦系數的因數很多,如正壓力的大小、接觸時間、平滑程度、潤滑情況、滑動速度等。由于斜拉索內高強鍍鋅平行鋼絲每層鋼絲平均受到正壓力的大小不相同[2],故筆者在研究中主要考慮正壓力大小對平行鋼絲摩擦系數值的影響,其它影響因素暫不予考慮。
1 正壓力對摩擦系數的影響
根據固體力學相關知識,表觀接觸面積一定時,正壓力N越大,實際接觸面積S0越大,并和正壓力成正比:

式中:S0為實際接觸面積;s為正壓力為0時的實際接觸面積;N為正壓力;ΔS0為實際接觸面積增量;ΔN為正壓力增量。
設單位實際接觸面積上的分子引力P0,則接觸面上的合分子引力為:

它相當于物體增加了重量負載,等效正壓力Neff為:

根據摩擦二項式定律,滑動摩擦力fr和等效正壓力Neff成正比,即:
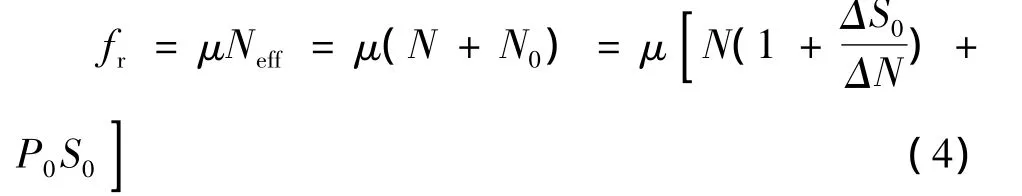
式中:fr為滑動摩擦力;μ為摩擦系數;Neff為等效正壓力;P0為分子引力;N0為接觸面上的合分子引力;其他符合同前。
由摩擦二項式定律即式(4)可得:

而一般意義的摩擦系數為:
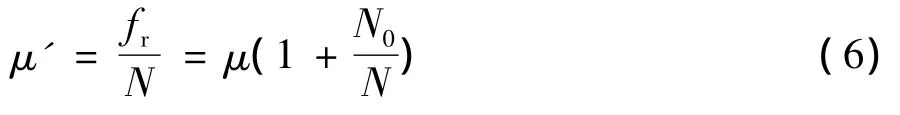
即,表觀摩擦系數隨著正壓力N的增大而減小,從而不是恒量[3]。蔣浩民,等[4]采用平板摩擦試驗研究了正壓力對鍍鋅鋼板摩擦系數的影響,實驗證實了摩擦系數隨著正壓力N的增大而減小。
總之,正壓力對摩擦系數的影響與實際接觸面積有關,一般情況下是摩擦系數隨正壓力增加而降低,然后趨于穩定[5]。
2 實驗方法
2.1 加壓方式及實驗裝置的確定
本實驗裝置是在此前實驗裝置的基礎上經設計改裝而成的,利用此前實驗所用的1#、2#兩塊鋼槽固定鋼絲,如圖1。
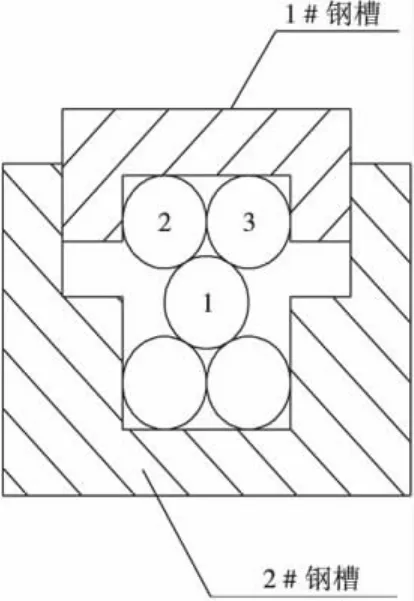
圖1 實驗所用1#、2#鋼槽Fig.1 The 1#,2#steel tank used in experiments
采用兩枚M10×200螺栓對鋼槽均勻地施加正壓力,為了較精確地給螺栓加壓,采用螺距為1mm的M10標準螺距螺栓[6]。實驗裝置如圖2。
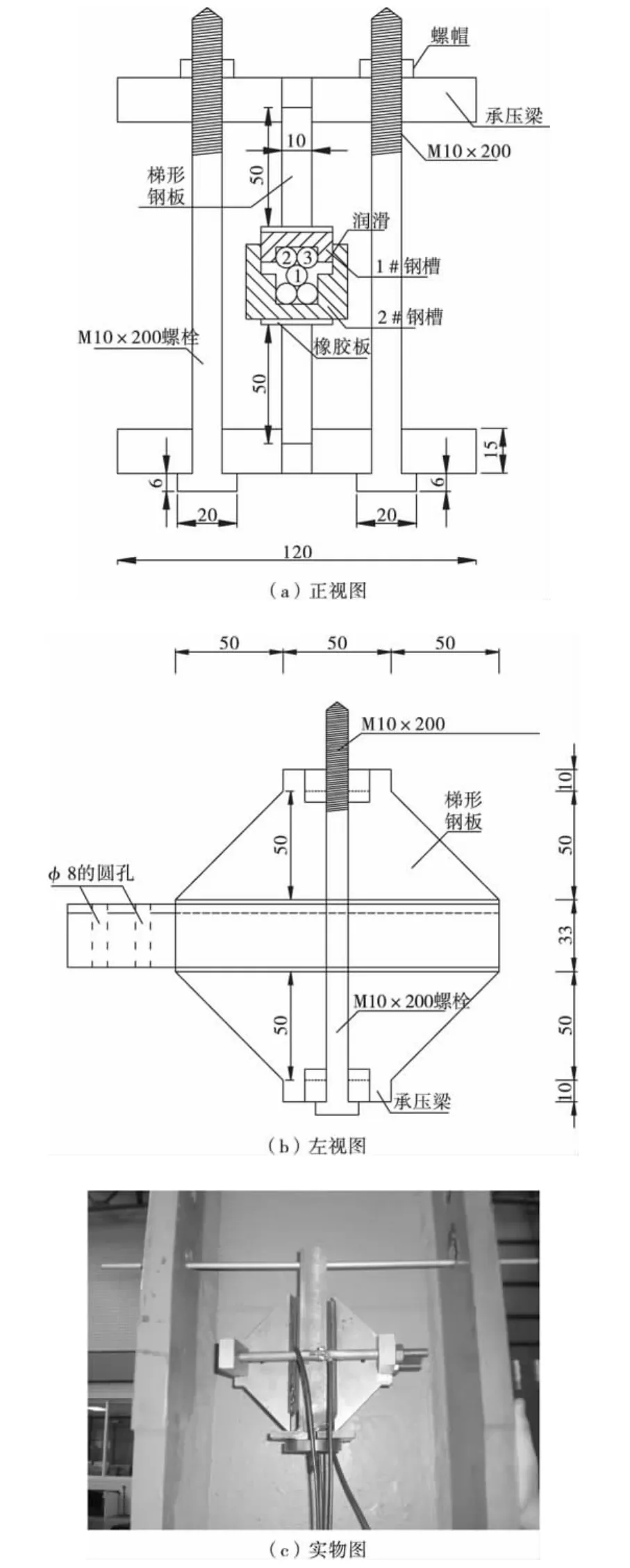
圖2 實驗裝置Fig.2 Experimental device
將兩根M10螺栓螺桿穿過自制的承壓梁,并將螺母栓在螺桿上。用扳手擰螺母時,螺母對承壓梁產生壓力,此壓力將通過梯形鋼板傳遞至鋼槽上,從而實現對鋼槽內鋼絲的加壓。試驗中,設置梯形鋼板的目的是為了實現對鋼槽的均勻加壓,根據力基本沿45°方向傳遞原則,將梯形鋼板設計成兩底角為45°[圖2(b)]。在梯形鋼板和鋼槽之間放置橡膠板,目的是防止加壓過程中梯形鋼板與鋼槽之間的打滑,且有利于將梯形鋼板所受到的的力均勻傳遞至鋼槽。在試驗中,為了使整個裝置能夠懸掛起來,在1#和2#上挖兩個 φ8的孔[圖2(b)]。
把裝置懸掛起來[圖2(c)],當用扳手擰緊螺帽時,產生的壓力通過承壓梁一直傳至梯型鋼板,通過梯型鋼板對鋼槽均勻加力。在加壓過程中,較難控制螺栓對鋼槽所加的力的大小。但明顯的,當對螺栓加壓時,螺栓會因此而產生相應的應變。所以,為了較精確地控制螺栓加力的大小,在螺栓中部位置黏貼電阻應變片,螺栓上應變片布置如圖3。通過電阻應變片測得的鋼筋的平均應變值,由應變值可反算出所加壓力值的大小,此壓力值也可視為螺栓對承壓梁所加的壓力值,也為螺栓對鋼槽所加的壓力值。
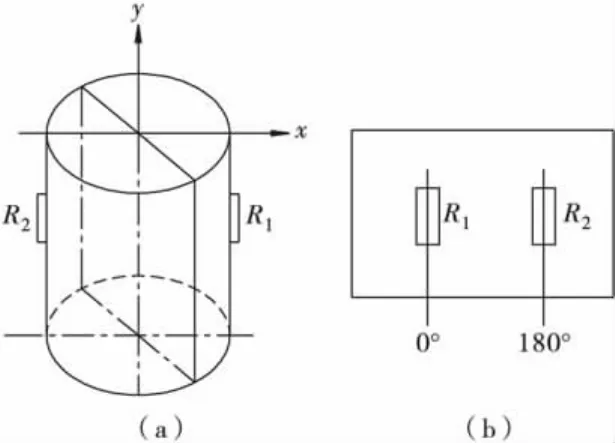
圖3 螺栓的應變片布置Fig.3 Strain gauge on the bolt arrangement figure
2.2 加壓值的大小
經過層間累加之后,內層單根鋼絲間擠壓力可高達40 kN/m[7]。由試驗用鋼絲的受力長度 10 mm,確定出對1#鋼絲加壓范圍為300~4 000 N,在此壓力范圍加壓,足以模擬斜拉索實際工作中拉索的真實受力狀態了。在300~4 000 N范圍內,對應各個級別的正壓力,分別進行拉拔實驗,得出相應的鋼絲摩擦系數值。本次實驗中,由于時間和精力有限,在所得數據在統計上有一定保證率的前提下,將所加正壓力300~4 000 N范圍分成17個級別,分別進行了拉拔實驗。
3 實驗開展與結果討論
3.1 實驗開展
本實驗測試螺栓應變所用的應變片為電阻位為120 Ω的BE120-4AA的應變片,靈敏度 K=2.23±0.01。將兩張應變片對稱地布置在用于加力的螺栓的中部(圖3)。為了進行溫度補償,取一螺栓,在其上黏貼補償片(補償片的布置如圖4、圖5)。

圖4 補償片上應變片布置Fig.4 Strain gauge on the compensator arrangement figure

圖5 補償片上應變片布置實物Fig.5 Strain gauge on the compensator physical map
本實驗利用美國DEWE-501數據采集系統進行應變的采集,實驗采用單倍電橋接線法接線。實驗方案布置如圖6。

圖6 實驗方案布置Fig.6 Experimental arrangement
3.2 實驗結果討論
根據實驗數據得出斜拉索高強鍍鋅平行鋼絲摩擦系數隨正壓力變化的變化趨勢如圖7。

圖7 摩擦系數隨正壓力變化的變化趨勢Fig.7 Friction coefficients changing with the positive pressure
從圖7可看出:隨著正壓力的增大,高強鍍鋅鋼絲的摩擦系數值總體上成下降趨勢。此實驗結果與理論推導得出的結論——表觀摩擦系數不是恒量,而是隨著正壓力的增大而減小——是相吻合的。隨著正壓力的增大,一直增大到1 700 N附近,高強鍍鋅鋼絲的摩擦系數值下降十分顯著,可能的原因是由于一定的正壓力有助于鋼絲與鋼絲之間達到良好的潤滑并抑制表面的粗糙。但當壓力繼續增大,直到4 000 N左右時,圖中出現了一段非常平緩的下降段。即當正壓力增大到較大值時摩擦系數的降幅明顯減緩了。出現此下降段的原因可能是:隨著壓力的繼續增加,鋼絲與鋼絲之間的接觸面積會有所增加,在較高壓力下鍍鋅層對摩擦系數的影響已經明顯減小了。
4 結論
筆者利用自行設計的裝置對鋼絲施加一定的正壓力。測定出一定壓力下一系列鋼絲間的摩擦系數值,描述出摩擦行為表現和摩擦系數變化趨勢為:隨著正壓壓力的增大,斜拉索內高強鍍鋅平行鋼絲的摩擦系數明顯降低,但當壓力增大到較大值時摩擦系數的降幅明顯減緩。
[1]李紅,鄭罡,陳璨.斜拉索內平行鋼絲間摩擦系數的確定[J].重慶交通大學學報:自然科學版,2011,30(2):196-199.Li Hong,Zheng Gang,Chen Can.Determination of friction coefficients between steel wires in stay cables[J].Journal of Chongqing Jiaotong University:Natural Science,2011,30(2):196-199.
[2]Zheng Gang,Li Hong.Normal stress between steel wires in the stay-cable[J].Applied Mechanics and Materials Journal,2011,50/51:541-546.
[3]劉亞民.摩擦力與摩擦系數的幾點性質[J].烏倫貝爾學院學報,2006,14(4):67 -68.Liu Yamin.Some qualities of friction and friction modulus[J].Journal of Hulunbeier College,2006,14(4):67-68.
[4]蔣浩民,陳新平,俞寧峰,等.正壓力和滑動速度對鍍鋅鋼板摩擦系數的影響[J].鍛壓技術,2005,30(增刊1):129 -132.Jiang Haomin,Chen Xinping,Yu Ningfeng,et al.Effects of contact pressure and sliding velocity on the frictional coefficient of zinccoated sheets[J].Forging & Stamping Technology,2005,30(supp1):129-132.
[5]賈毅朝,摩擦與摩擦系數的分析[J].運城學院學報,2006,24(2):60-61.Jia Yichao.Analysis of friction and friction factors[J].Journal of Yuncheng University,2006,24(2):60-61.
[6]GB/T 5782—2000六角頭螺栓[S].北京:中國標準出版社,2001.
[7]李紅.斜拉索內鋼絲間聯合工作模式對局部彎曲應力的影響[D].重慶:重慶交通大學,2010.
[8]黃平.摩擦學教程[M].北京:高等教育出版社,2008.
[9]PTI.Recommendation for Stay Cable Design,Testing and Installation[R].Phoenix,Arizona:Post-Tensioning Institute,2001.
[10]楊駿,王剛雷,黃瑤.電鍍鋅板摩擦系數的影響因數分析[J].精密成形工程,2009,1(3):14 -17.Yang Jun,Wang Ganglei,Huang Yao.The analysis on the influence factors of frictional coefficient of zinc-coated sheet[J].Journal of Netsshape Forming Engineering,2009,1(3):14-17.
[11]楊興,張敏,周水興.影響矩陣法在斜拉橋二次調索中的應用[J].重慶交通大學學報:自然科學版,2009,28(3):508 -511.Yang Xing,Zhang Min,Zhou Shuixing.Application of influence matrix method to secondary cable-adjustment of cable-stayed bridges[J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(3):508-511.

