應用總應變-應變能區分法預測熱機械疲勞壽命
胡緒騰,宋迎東
應用總應變-應變能區分法預測熱機械疲勞壽命
胡緒騰,宋迎東
(南京航空航天大學機械結構力學及控制國家重點實驗室,江蘇南京210016)
簡要介紹了總應變-應變能區分法(TS-SEP)的基本假設和基本方程,應用TS-SEP法對三種金屬材料(304不銹鋼、1Cr-1Mo-0.25V鋼和2.25Cr-1Mo鋼)的熱機械疲勞試驗數據進行了分析和預測,初步評估了TS-SEP法對熱機械疲勞數據的相關和預測能力。研究結果表明:TS-SEP法與總應變-應變范圍區分法(TS-SRP),對三種金屬材料的熱機械疲勞試驗數據具有相當的相關和預測能力,壽命預測分散帶均在2倍范圍內。
熱機械疲勞;蠕變-疲勞;壽命預測;總應變-應變能區分法;應變能區分法;應變范圍區分法
1 引言
許多熱機械結構的疲勞失效本質上是熱機械疲勞所致,例如航空發動機渦輪葉片在使用中即承受著復雜的熱機械循環載荷作用。由于熱機械疲勞試驗的困難,長期以來未形成統一的熱機械疲勞試驗標準[1],傳統上材料的熱機械疲勞抗力,通常通過在熱機械循環的最高溫度下開展等溫疲勞試驗來估計,而蠕變效應則通過在最大拉伸或壓縮應變上施加保載來實現[2]。因此,等溫蠕變-疲勞在近50年來得到了較多研究。針對等溫蠕變-疲勞,國內外學者已提出和發展了100多種蠕變疲勞壽命預測方法,但只有少數幾種方法得到了廣泛應用[3],其中包括由Manson、Halford等發展的應變范圍區分法(SRP)[4]和總應變-應變范圍區分法(TS-SRP)[5,6]——這兩種方法在美國航空航天工業界已獲得實際應用。一些等溫蠕變-疲勞壽命預測方法也被試圖用于熱機械疲勞,如Halford和Manson[7]曾應用SRP法預測熱機械疲勞壽命。上世紀90年代,Saltsman和Halford又對基本的TS-SRP法進行了適當修正,發展了針對熱機械疲勞的TMF/TS-SRP法,取得了較好的效果[8]。
我國學者何晉瑞等[9]于上世紀80年代基于SRP法和Ostergren拉伸滯后能的觀點,提出了應變能區分法(SEP),較SRP法提高了壽命預測精度。近年來,本文作者借鑒Halford和Saltsman發展TS-SRP法的經驗,將SEP法推廣到總應變形式,發展了總應變-應變能區分法(TS-SEP),拓展了SEP法的適用范圍,特別是低應變、長壽命范圍的蠕變-疲勞壽命預測[10]。本文試圖進一步將TS-SEP法推廣應用于熱機械疲勞壽命分析,對其預測能力進行分析和研究。
2 TS-SEP法的基本假設和基本方程
TS-SEP法由SEP法發展而來,而SEP法又是從SRP法發展而來。因此,其基本思想仍然是對典型的高溫疲勞滯后回線進行分析。按照拉、壓加載方向的不同及蠕變與塑性應變的區別,將總的非彈性應變范圍Δεin區分為四種基本的應變范圍分量(見圖1):①PP型應變分量Δεpp,正向為拉伸塑性應變,反向為壓縮塑性應變,即純塑性循環;②PC型應變分量Δεpc,正向為拉伸塑性應變,反向為壓縮蠕變;③CP型應變分量Δεcp,正向為拉伸蠕變,反向為壓縮塑性應變;④CC型應變分量Δεcc,正向為拉伸蠕變,反向為壓縮蠕變。與SRP法和TS-SRP法不同的是,SEP法和TS-SEP法在分析時將上述應變分量轉變為相應的拉伸應變能分量。
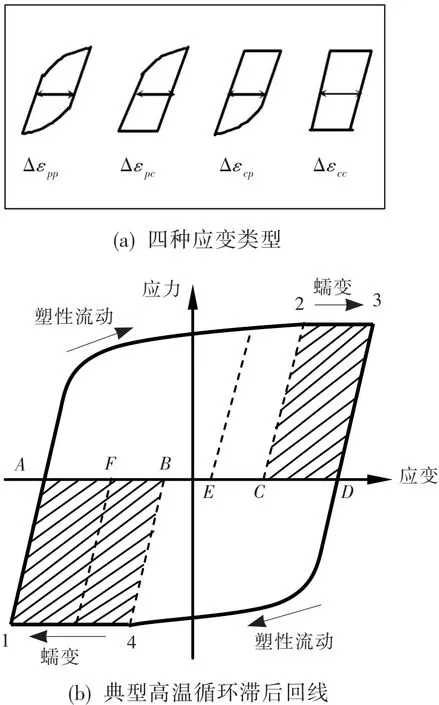
圖1 基本應變類型和典型高溫疲勞循環滯后回線Fig.1 Basic strain range and typical high temperature fatigue hysteresis loop
TS-SEP法在SEP法基礎上建立了高溫疲勞循環總應變范圍Δεto與循環壽命Nf之間的關系:
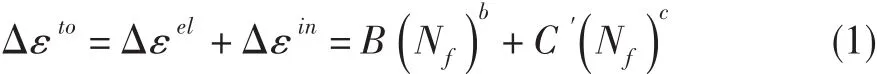
其中Δεin與Nf之間的關系,是對SEP法基本方程做適當改進(假設在雙對數坐標系內,CP、PC、CC三種類型的應變能分量-壽命方程平行于PP型應變能分量-壽命方程)后,結合交互作用損傷法則推導得到。系數C′為:

式中:壽命指數c和系數Cij(ij=PP,CP,PC,CC)為材料常數,σT為疲勞循環的峰值拉伸應力,(ij=PP,CP,PC,CC)為應變能分量分數。
彈性應變范圍Δεel與Nf之間的關系,通過建立Δεel與Δεin之間的經驗關系,結合已建立的非彈性應變范圍-壽命關系獲得。假設在雙對數坐標系內,復雜高溫循環的彈性應變范圍-非彈性應變范圍,方程平行于純疲勞循環(即PP型循環)的彈性應變范圍-非彈性應變范圍方程,則有:

式中:應變硬化指數n和KPP為由PP型循環試驗數據擬合獲得的材料常數。將非彈性應變范圍-壽命關系代入方程(3),即獲得彈性應變范圍-壽命關系的系數B和指數b:

σT、(ij=CP,PC,CC)、Kij(ij=CP,PC,CC)則假設由下面的經驗公式確定:
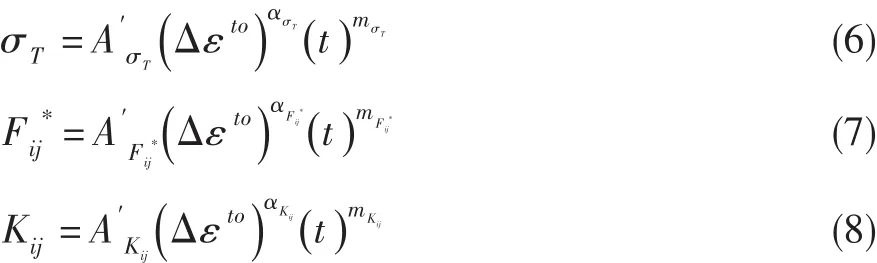
式中:t為單個高溫循環中的載荷保持時間,A′、α和m為根據材料流動行為(循環變形)試驗數據擬合得到的材料常數。
TS-SEP法建立和推導的詳細過程可參考文獻[10]。本文假設將TS-SEP法應用于熱機械疲勞,具有與上述相同的基本假設和基本方程。
3 TS-SEP法對熱機械疲勞壽命的預測能力
Saltsman和Halford[8]采用三種金屬材料(304不銹鋼、1Cr-1Mo-0.25V鋼和2.25Cr-1Mo鋼)的熱機械疲勞試驗數據,對TS-SRP法的熱機械疲勞預測能力進行了評估。本文采用相同的試驗數據對TS-SEP法的熱機械疲勞壽命預測能力進行初步評估,并與TS-SRP法的預測結果進行對比。
304不銹鋼的試驗數據包括同相連續熱機械循環(PP型)、同相拉伸應變保持熱機械循環(CP型)和反相壓縮應變保持熱機械循環(PC型),溫度循環范圍有200~550℃和300~600℃兩種。其中反相保持熱機械循環相對于反相熱機械循環壽命無顯著變化,文獻[8]沒采用,本文也不采用。1Cr-1Mo-0.25V鋼的試驗數據只包括同相連續熱機械循環(PP型)和同相拉伸應變保持熱機械循環(CP型),溫度循環范圍300~550℃。2.25Cr-1Mo鋼的試驗數據包括同相和反相連續熱機械循環(PP型)、同相拉伸應變保持熱機械循環(CP型)和反相壓縮應變保持熱機械循環(PC型),溫度循環范圍為300~538℃。2.25Cr-1Mo鋼還包括反相快/慢循環和同相慢/快循環試驗數據,溫度循環范圍為360~600℃。根據上述三種材料的熱機械疲勞試驗數據,擬合獲得了相應的TS-SEP法材料常數,結果見表1。
由于三種材料的試驗數據相對有限,本文只對用于估計材料參數的基本試驗數據進行預測分析。采用下面定義的預測分散帶和對基本試驗數據的相關能力來描述TS-SEP法的預測能力。
壽命預測分散帶定義為:
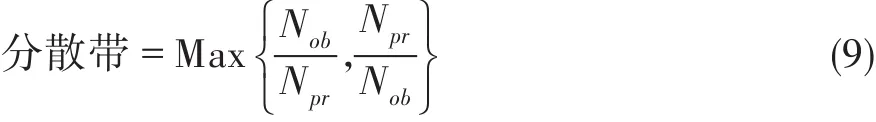
對基本試驗的相關能力采用標準差來定義:
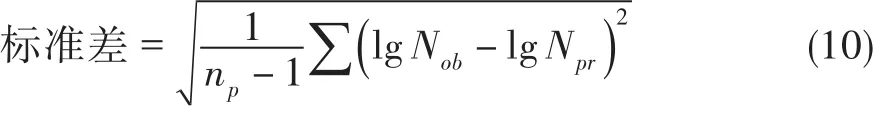
式中:Nob為試驗壽命,Npr為預測壽命,np為基本試驗數據點個數。
TS-SEP法和TS-SRP法的預測結果見表2。其中TS-SRP法沒有考慮平均應力效應。從表中結果可以看出,TS-SEP法對三種材料基本試驗數據的相關能力和預測效果均較好,好于不考慮平均應力的TS-SRP法。文獻[8]應用TS-SRP法預測時考慮了平均應力效應,預測結果為:304不銹鋼的最大預測分散帶為1.26,1Cr-1Mo-0.25V鋼的最大預測分散帶為1.87,2.25Cr-1Mo鋼的最大預測分散帶為1.56。可見,TS-SEP法與TS-SRP法對上述三種材料的熱機械疲勞試驗數據具有相當的預測和相關能力,壽命預測分散帶均在2倍范圍內。
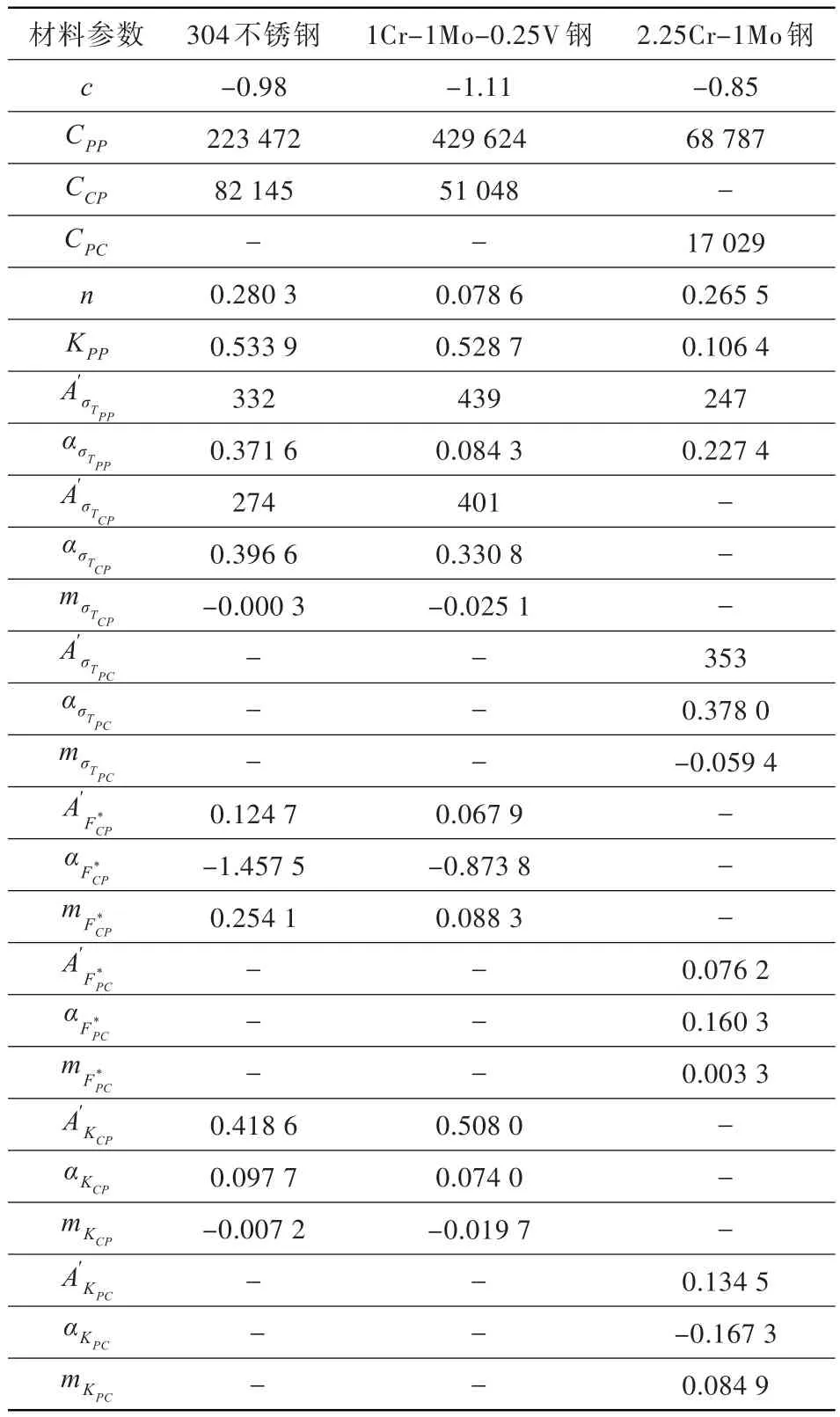
表1 三種材料的TS-SEP法材料常數Table 1 TS-SEP material parameters of three materials
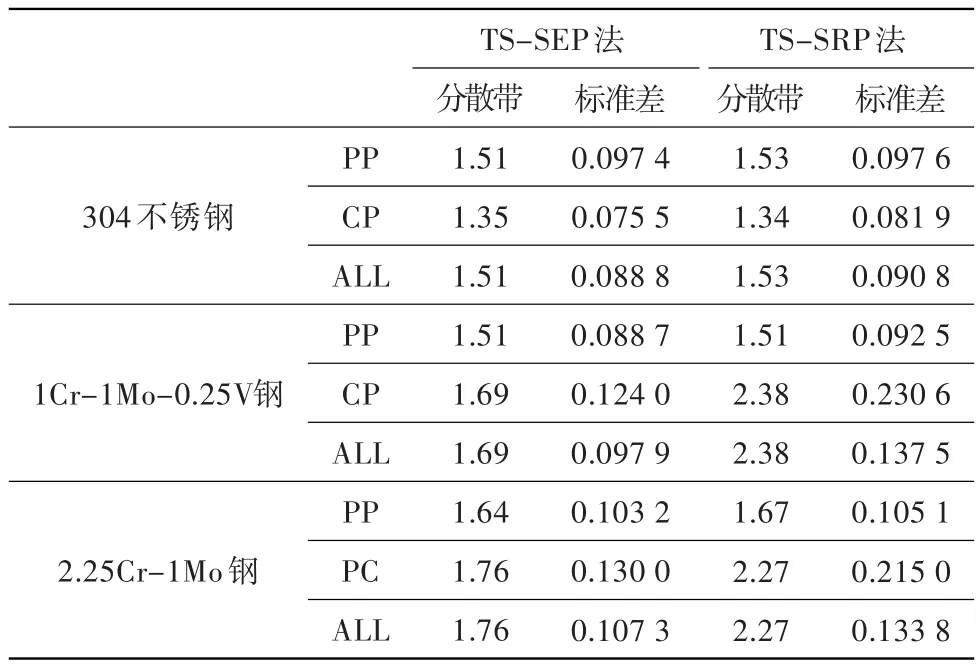
表2 TS-SEP法與TS-SRP法的預測結果對比Table 2 Comparison of life prediction results of TS-SEP and TS-SRP
4 結束語
本文采用TS-SEP法對三種金屬材料的熱機械疲勞試驗數據進行了預測分析。結果表明,TS-SEP法與TS-SRP法對三種金屬材料熱機械疲勞試驗數據具有相當的相關和預測能力,壽命預測分散帶均在2倍范圍內,顯示出TS-SEP法應用于熱機械疲勞壽命預測的潛力。但由于試驗數據相對有限,僅對用于估計材料參數的試驗數據進行了預測,所以今后仍需就TS-SEP法對高溫疲勞(包括等溫蠕變-疲勞和熱機械疲勞)的預測能力做進一步驗證和評估。
[1]Hahner P,Bressers J.Thermo-Mechanical Fatigue:the Route to Standardization[J].Materials at High Tempera?tures,2002,19(4):235—240.
[2]Saltsman J F,Halford G R.Life Prediction of Thermome?chanical Fatigue Using the Total Strain Version of Strain?range Partitioning(SRP)-A Proposal[R].NASA TP-2779,1988.
[3]Halford G R.Evolution of Creep-Fatigue Life Prediction Models[C]//.Haritos G K,Ochoa O O.In Creep-Fatigue Interaction at High Temperature.ASME,1991,AD-21:43—57.
[4]Manson S S,Halford G R,Hirschberg M H.Creep-Fa?tigue Analysis by Strain-Range Partitioning[C]//.Zamrik S Y.In Design for Elevated Temperature Environment. ASME,1971:12—28.
[5]Halford G R,Saltsman J F.Strainrange Partitioning-A To?tal Strain Range Version[C]//.Woodford D A,Whitehead J R.Advances in Life Prediction Methods.ASME,1983:17—26.
[6]Saltsman J F,Halford G R.An Update of the Total Strain Version of SRP[C]//.Solomon H D,Halford G R,Kaisand L R,et al.Low Cycle Fatigue-Directions for Future. ASTM STP-942.ASTM,1988,329—341.
[7]Halford G R,Manson S S.Life Prediction of Thermal-Me?chanical Fatigue Using Strainrange Partitioning[R].NASA TM X-71829,1975.
[8]Saltsman J F,Halford G R.Ability of the Total Strain Ver?sion of Strainrange Partitioning to Characterize Thermome?chanical Fatigue Behavior[R].NASA TM-4556,1994.
[9]He J,Duan Z,Ning Y,et al.Strain Energy Partitioning and Its Application to GH33A Nickel-Base Superalloy and 1Cr18Ni9Ti Stainless Steel[C]//.Woodford D A,Whitehead J R.Advances in Life Prediction Methods. ASME,1983:27—32.
[10]胡緒騰,宋迎東.總應變-應變能區分法[J].機械工程學報,2007,43(2):219—224.
Life Prediction for Thermomechanical Fatigue Using Total Strain Version of Strain Energy Partitioning
HU Xu-teng,SONG Ying-dong
(State Key Laboratory of Machinery Structural Mechanics and Control,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
The basic concepts and equations of Total Strain Version of Strain Energy Partitioning(TS-SEP) are introduced briefly.Then the correlative and predictive capabilities of TS-SEP to thermomechanical fa?tigue(TMF)data of three metals(Type 304 Stainless Steel,1Cr-lMo-O.25V Steel and 2.25Cr-lMo Steel)in the literature are evaluated.The result indicates that TS-SEP and Total Strain Version of Strain Range Par?titioning(TS-SRP)have comparative correlative and predictive capabilities with the TMF data of three steels.The maximum life prediction scatter bands of two methods are both less than 2.0.
thermomechanical fatigue;creep-fatigue;life prediction;TS-SEP;SEP;SRP
O346.2
A
1672-2620(2012)01-0014-03
2011-06-15;
2011-11-25
胡緒騰(1980-),男,江蘇沛縣人,講師,博士,主要從事結構強度、耐久性、損傷容限等方面的研究。

