脈沖擾動系統的集合穩定性

趙海清，張玉樂，王光雪

(大連交通大學 理學院，遼寧 大連 116028)＊

0 引言

人口動態，細胞分裂等一些數學模型都用脈沖系統來描述，因此近年來脈沖系統理論被廣泛研究和發展.脈沖系統理論形成了很多不同的穩定性概念，如嚴格穩定性［1］，實際穩定性［2］以及兩測度穩定性［3］等等.另外，由于實際到一個數學模型有時總有一些誤差，而且由于機器老化等一些實際問題，使得一些模型總是有一些擾動存在.如果我們考慮這些擾動，便產生了一個擾動系統.對原來的無擾動系統，它通常需要滿足某種穩定性，那么它所對應的擾動系統是否是穩定的呢?這需要我們進一步判斷.可是不幸的是，我們除了知道擾動項的一些定性的信息，如擾動的范數的上界等條件，根本不知道擾動項的具體描述，因此我們就不能用已有的穩定性方法來判斷.本文從擾動項上界這僅有的條件出發，研究了擾動脈沖微分系統的集合穩定性.之所以研究集合穩定性，是因為集合穩定性是包含零解的穩定性，解的穩定性的比較廣泛的穩定性概念［4］.

具體地，我們是利用原始脈沖系統的穩定性和Lyapunov函數，考慮到擾動項的影響，研究了脈沖系統的集合的一致漸近穩定性，給出了集合穩定的充分性條件.本文的方法可以用來考慮一個復雜的脈沖系統的穩定性，只要把這個復雜的脈沖系統看成我們熟悉的或者能判斷其穩定性的系統的擾動系統，根據我們定理的條件，便可以判斷出這個復雜系統的穩定性.

1 研究系統及相關知識

Rn是一個定義了范數和距離的n維歐式空間.我們考慮下面這個擾動系統

式中，t∈R+=［0，+∞)，x∈Rn，f:R+×Rn→Rn關于自變量t是逐段連續，在每個tk點左連續，Ik(x):Rn→Rn關于每個k連續，0＜t1＜t2＜… ＜tk＜…，當 k→ ∞，tk→ ∞，Δx(tk)=Ik(x(tk))+Jk(x(tk))，系統(1)是如下系統(2)的一個擾動系統

由于模型的偏差，機器老化等實際問題產生了擾動項g(t，x)，Jk(x)，有時我們不知道擾動項的具體表達或其一些定量性質，但是我們知道擾動項的范數的上界.本文將利用這個上界來解決擾動系統的一致漸近穩定問題.令x(t;t0，x0)是具有初值x()=x0的(1)的解.

定義下面的類

K={a|a:R+→R+是關于自變量嚴格遞增的函數且a(0)=0};

Gk={(t，x)∈ R+× Rn，tk－1＜ t ＜ tk，且 tk預先給定};

M(t)={x∈ Rn:(t，x)∈ M};

M(t，ε)={x∈ Rn:d(x，M(t))＜ ε，ε ＞ 0};

Dη，t={x∈Rn:d(x，M(t))≤η，η＞ 0，t∈R+};

Sα={x∈ Rn:‖x‖ ＜ α，α ＞ 0}.

假設

(1)?t∈R+，M(t)不是空集;且存在緊集Q?Rn，使得M(t)? Q;

(2)對(t，x)，(t'，x)∈f+g，存在常數ρ使得|d(x，M(t))－ d(x，M(t＇))|≤ ρ|t－ t'|;

(3)對系統(1)的每個解滿足:任意定義域內的 t，d(x(t;t0，x0)，M(t))≤ r ＜ ∞.

定義1 函數V:R+×Rn→R+屬于ν0，下面的條件被滿足

(2)在每個tk處 V是左連續的且右極限存在，特別是，當(t，x)∈ M 時，V(t，x)=0，否則，V(t，x)＞ 0.

定義3［5］如果下面的條件(1～3)成立，則關于系統(1)的集合M是一致全局漸近穩定的.

(i)M是穩定的:?t0∈R+，?ε＞0和?α＞0，存在 δ(ε)＞ 0和?x0∈Sa∩M(t0，δ)使得對t≥ t0，x(t)∈ M(t，ε);

(ii)系統(1)的解是有界的:?t0∈R+，?η＞0和 ?α ＞ 0，存在β(ε)＞ 0和?x0∈Sa∩Dη，t0使得對 t≥ t0，x(t)∈ M(t，β);

(iii)M是吸引的:?t0∈R+，?η ＞0，?α ＞0和?ε ＞ 0存在T(η，ε)＞ 0和?x0∈Sa∩Dη，t0使得對 t≥ t0+T，x(t)∈ M(t，ε).

2 穩定性證明

引理 假設對t≥t0，m(t):R+→R在tk上左連續，對任意的k，D+m(t)≤l(t)m(t)+p(t)，m)≤ekm(tk)+qk，則，其中l(t)，p(t)是連續的，ek，qk是常數.

定理 設 a，b，c∈ K，λ(t)，θ(t)是可積正函數，且下面條件成立:

(i)a(d(x，M(t)))≤ V(t，x)≤ b(d(x，M(t)))，(t，x)∈ R+× Rn;

(ii)對系統(2)中的V(t，x)滿足D+V(t，x)≤－ λ(t)V(t，x)，t≠ tk和 V(t+0，x+ Δx)≤ V(t，x)，t=tk;

(iii)||g(t，x)||≤ θ(t)a(d(x，M(t)))，且Lθ(t)＜ λ(t);

(iv)||Jk(x(tk))||≤ εka(d(x(tk)，M(tk)))，εk≥0和Lεk＜ ∞.

則M是系統(1)的一個一致全局漸近穩定集.

對 t≠ tk，

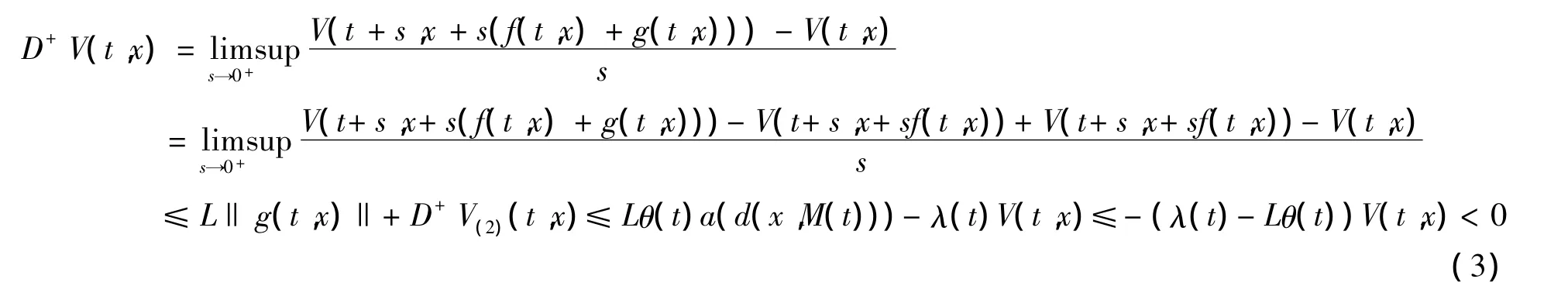
對t=tk，

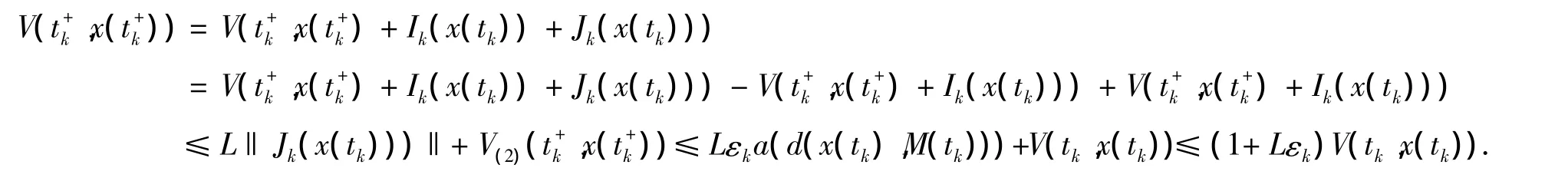
根據引理有

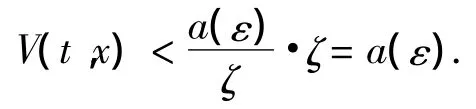
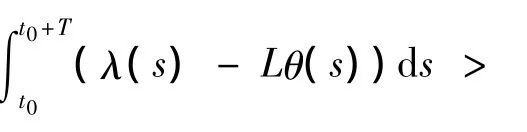
下面我們將證明對上面的T(η，ε)＞0，系統(1)的解滿足對?α ＞ 0，x0∈Sα∩Dη，t0，存在t*∈［t0，t0+T］，使得 d(x(t*)，M(t*))＜ δ.否則，對任意 T ＞ 0，t∈［t0，t0+T］有d(x(t)，M(t))≥δ.

根據(3)，有下面的式子

這是一個矛盾，所以存在t*∈［t0，t0+T］，使得d(x(t*)，M(t*))＜ δ.

根據式(4)，

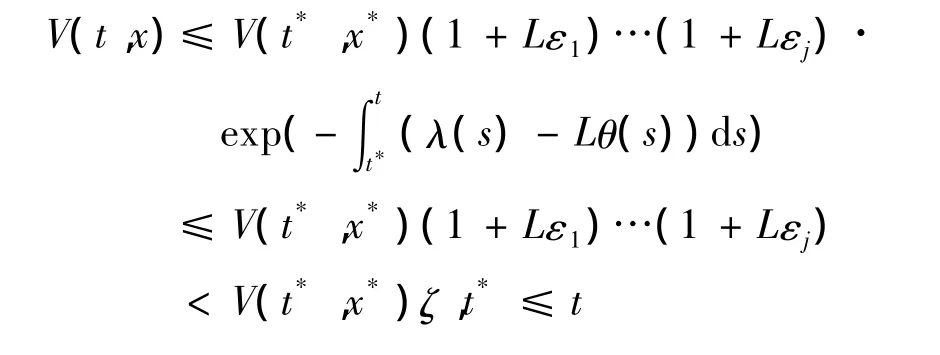
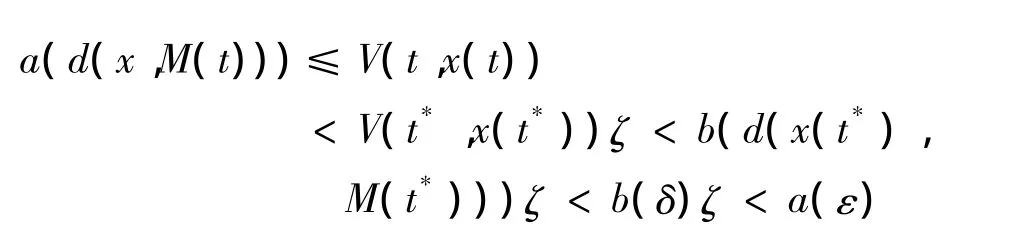
這就證明了M是一致全局吸引的.

對 ?α ＞ 0，?η ＞ 0，?x0∈ Sα∩ Dη，t0，取β(α，η)使 a(β(α，η))＞ b(η)ζ.根據式(4)和(i)，有

這就證明了系統(1)的解是有界的，完成了定理的證明.

3 結論

本文利用Lyapunov函數，通過原始系統的穩定性解決了脈沖擾動系統的集合的全局一致漸近穩定性，該穩定性是包含零解一致漸近穩定的穩定性，具有廣泛的意義，特別是，應用本文的穩定性條件能快速判斷一個擾動系統的穩定性，因為它有了一個直接的Lyapunov函數.

［1］SENLIN LI，XINYU SONG，AN LI.Strict practical stability of nonlinear impulsive systems by employing two Lyapunov-like functions［J］.Nonlinear Analysis，2008(9):2262-2269.

［2］BORYSENKO S D，SPERANZA TOSCANO.Impulsive differential systems:The problem of stability and practical stability［J］.Nonlinear Analysis，2009，71:1843-1849.

［3］XINZHI LIN，QING WANG.On stability in terms of two measures for impulsive systems of functional differential equations［J］.J.Math.Anal.Appl.，2007，326:252-265.

［4］LASALLE J P.The extent of asymptotic stability［J］.Proc.Nat.Acad.Sci.，1960，46:363-365.

［5］KULEV G V，BAINOV D D.Global stability of sets for systems with impulses［J］.Applied Mathematics and Computation，1987，38:99-115.