基于熱電耦合的10kV XLPE地下電纜群溫度場數(shù)值計算

王巧玲，楊玉平，梁永春

(1.河北科技大學信息科學與工程學院，河北 石家莊050018;2.河北科技大學理工學院，河北 石家莊050018;3.河北科技大學電氣信息學院，河北 石家莊050018)

引言

目前電力輸送大多采用地下電纜的形式，安裝地下電纜需要保證地下散熱條件不使電纜超溫而導致絕緣損壞，但是由于影響電纜傳熱的可變因素很多，電纜的載流量很難準確確定。

綜合目前國內(nèi)外的研究現(xiàn)狀，可將已有的電纜溫度場數(shù)值計算方法概括為有限元法、邊界元法、有限差分法［1-6］。對于多芯電纜，有限差分和邊界元法都存在電纜區(qū)域剖分困難的問題，而有限元法可以很好地解決這個問題。

電纜導體的電阻率是溫度的線性函數(shù)，而電阻率是影響電纜發(fā)熱量的重要因素，同時也是本文主要考慮的，即地下電纜群溫度場計算是一個熱電耦合問題。本文采用有限元法進行數(shù)值計算，同時利用迭代法實現(xiàn)熱電間接耦合，確定土壤直埋電纜的散熱和周圍土壤的溫度分布，并最終確定電纜的載流量。

1 基本原理

1.1 損耗計算公式

單回路土壤直埋電纜如圖1所示，整個區(qū)域為一個半無限大溫度場。電纜群水平直埋于地下700mm處，周圍填充沙土100mm，然后回填土壤。

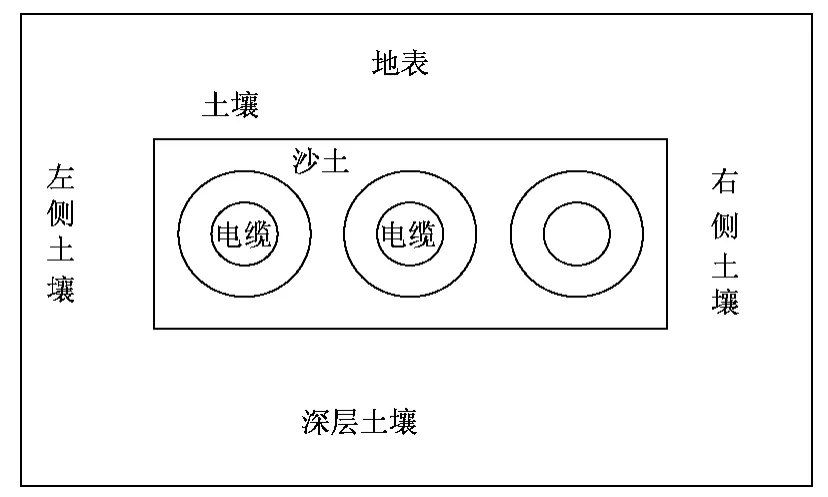
圖1 土壤直埋電纜物理模型Fig.1 Physical model of underground cables

整個區(qū)域為一個半無限大溫度場。需要將一個開域場轉(zhuǎn)變?yōu)殚]域場才能進行求解。上邊界為地表，屬于第三類邊界。下邊界、左邊界和右邊界可由以下方法確定。

溫度僅在電纜附近變化較為劇烈，當遠離電纜時，土壤溫度將與環(huán)境溫度相同。通常在距離電纜2000mm的土壤已不受電纜的影響。因此下邊界、左邊界和右邊界可取距離最近電纜3000mm的直線。圖1中左、右側(cè)土壤邊界為第二類邊界，深層土壤邊界為第一類邊界。

土壤直埋電纜線芯導體損耗、金屬屏蔽層損耗和鎧裝層損耗可以由電磁場計算而得。土壤直埋電纜的電磁場可以看作似穩(wěn)場處理，且電纜截面相對于長度很小，可以看作二維場計算損耗。二維直角坐標下的渦流損耗可以描述為［7-8］:

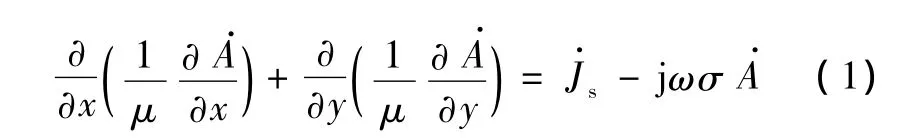
導體的損耗為:

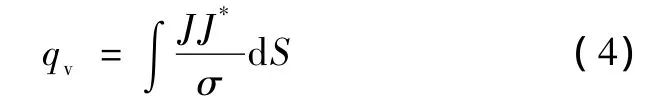
式中，qv為單位體積內(nèi)產(chǎn)生的熱量，W/m3。

絕緣介質(zhì)損耗可由IEC60287給定的公式計算。絕緣介質(zhì)損耗與電壓有關(guān)，每相中單位長度的絕緣損耗為:

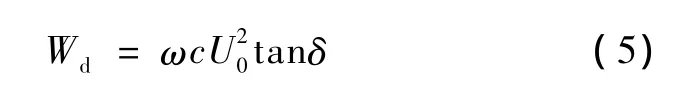
式中，U0為對地電壓(相電壓)，V;tanδ為在電源系統(tǒng)和工作溫度下絕緣損耗因數(shù);c為單位長度電纜電容，F(xiàn)/m。

圓形導體電容為:

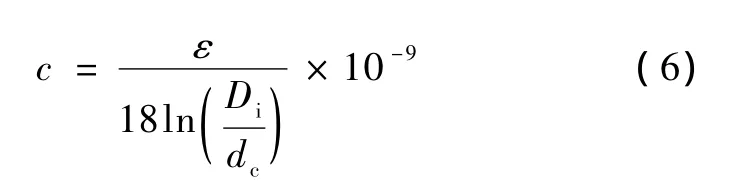
式中，ε為絕緣材料的介電常數(shù);Di為絕緣層直徑(屏蔽層除外)，mm;dc為導體直徑(如有屏蔽層則包含屏蔽層)，mm。

對于10kV以下電壓等級的電纜，絕緣介質(zhì)損耗很小，以6/10kV 150mm2YJV22型為例，絕緣介質(zhì)損耗約等于0.08W/m，在實際載流量計算中可以忽略不計。

1.2 溫度場計算公式

土壤直埋電纜的穩(wěn)態(tài)溫度場屬于二維穩(wěn)態(tài)導熱問題。有熱源區(qū)域(如電纜導體、金屬屏蔽層和鎧裝層)的溫度控制方程為:

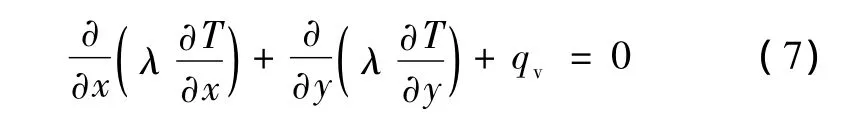
式中，T為點 (x，y)溫度，℃;λ為導熱系數(shù)，W/(m·℃)。

無熱源區(qū)域(如電纜其他層、土壤等)的溫度控制方程為:

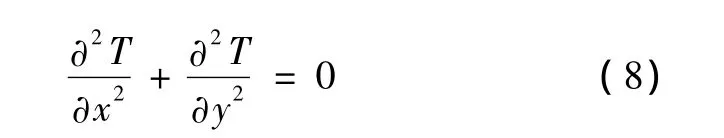
圖1中的三類邊界的控制方程為:

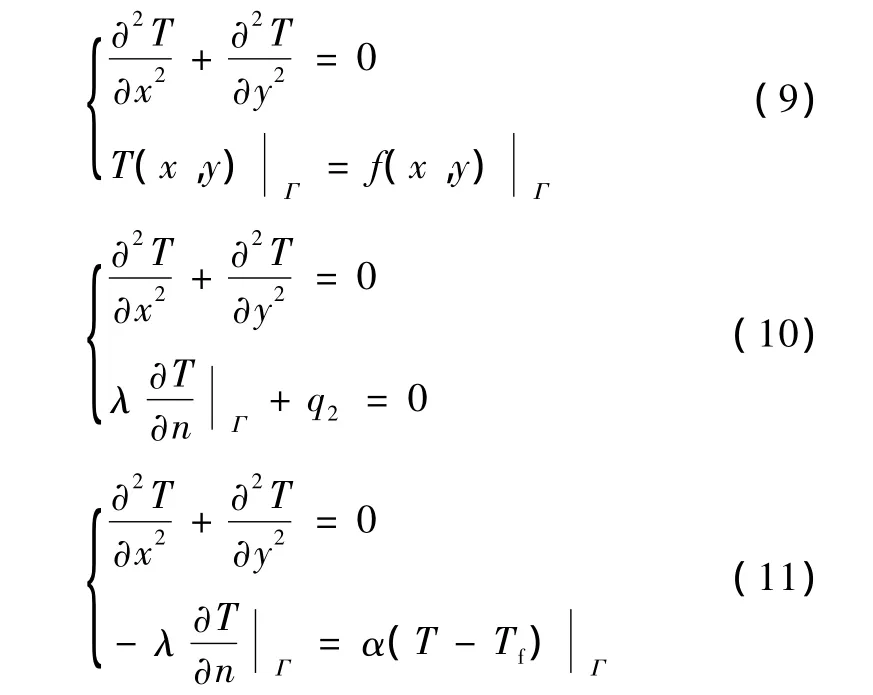
式中，q2為熱流密度，W/m2;α為對流換熱系數(shù);Tf為流體溫度，℃;Γ為積分邊界。

有限元計算溫度場中常用的計算單元為三角形單元。利用加權(quán)余量法和Galerkin法對式(7)～式(11)進行處理，整個區(qū)域的有限元方程為

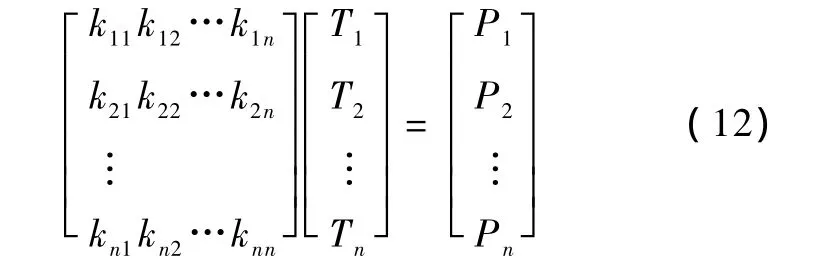
式中，kij、Pi(i=1 ～ n，j=1 ～ n，n是剖分節(jié)點數(shù))的計算參見文獻［8］。

利用迭代法對方程(2)求解，即可求得各點的溫度值。

2 耦合計算

在導體、金屬屏蔽層損耗和鎧裝層損耗計算中，qv為單位時間內(nèi)，在單位面積上產(chǎn)生的熱量，是溫度場計算的熱源，其數(shù)值由式(4)計算而得。而式(4)中的電導率σ是一個與溫度密切相關(guān)的量，可表示為:

式中，σ20為溫度為20℃時的電導率;Tr為導體的溫度，℃。

因而，直埋電纜溫度場計算是一個溫度場與電磁場耦合計算的問題，可由圖2所示迭代流程實現(xiàn)。

3 載流量的計算

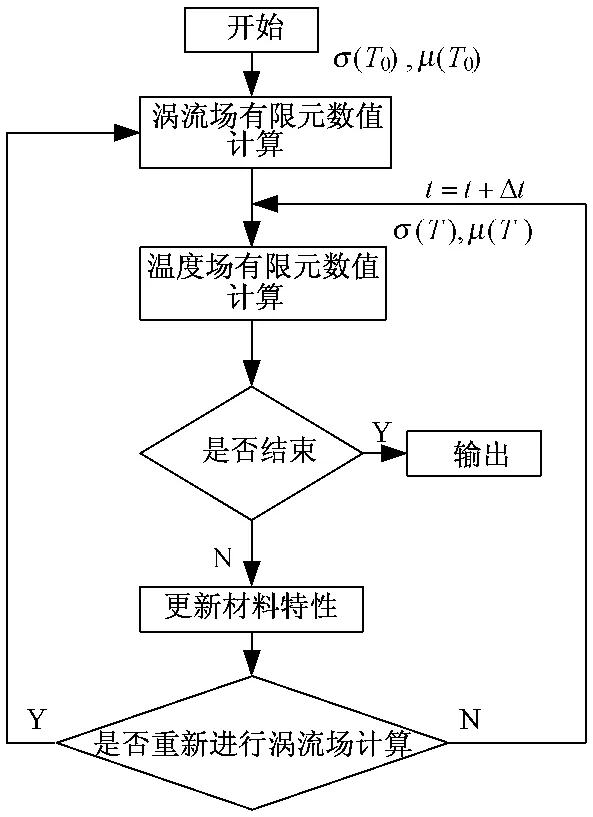
圖2 熱電耦合計算流程圖Fig.2 Flow chart of thermoelectric coupling

在給定電纜電流后，可根據(jù)圖2計算流程，利用有限元耦合計算電纜的溫度場。對于交聯(lián)聚乙烯電纜，要求長期工作過程中，導體溫度不超過90℃，此時可施加的最大負荷電流即為電纜的額定載流量。載流量的計算可根據(jù)圖3所示迭代過程計算。

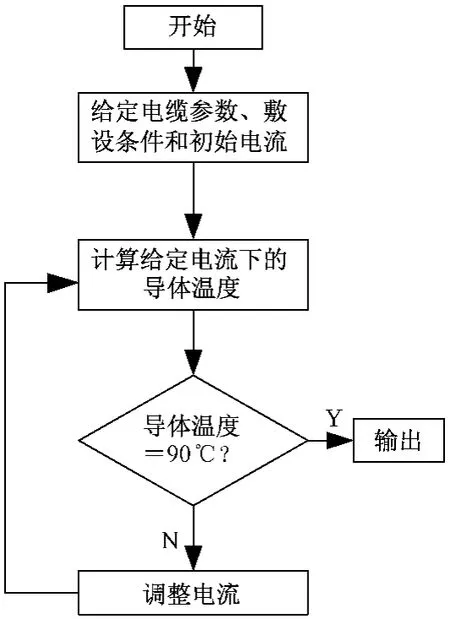
圖3 載流量計算流程圖Fig.3 Flow chart of ampacity calculation

4 模型仿真

以6/10kV 150mm2YJV22型XLPE電力電纜為例，計算電纜溫度場分布。電纜結(jié)構(gòu)參數(shù)如表1所示，敷設(shè)條件如表2所示。

電纜區(qū)域的有限元剖分模型如圖4所示。將邊界條件離散后，代入溫度場的有限元方程，采用交叉迭代法求解，得到整個電纜和周圍土壤溫度場的分布，整個考慮區(qū)域的溫度場對稱分布;最高溫度位于電纜區(qū)域，其導體溫度值為90℃。溫度從電纜到周圍土壤溫度逐步降低，距離電纜越遠，溫度越低，最后趨于恒定值，最后降到土壤溫度為10℃和地表溫度25℃。

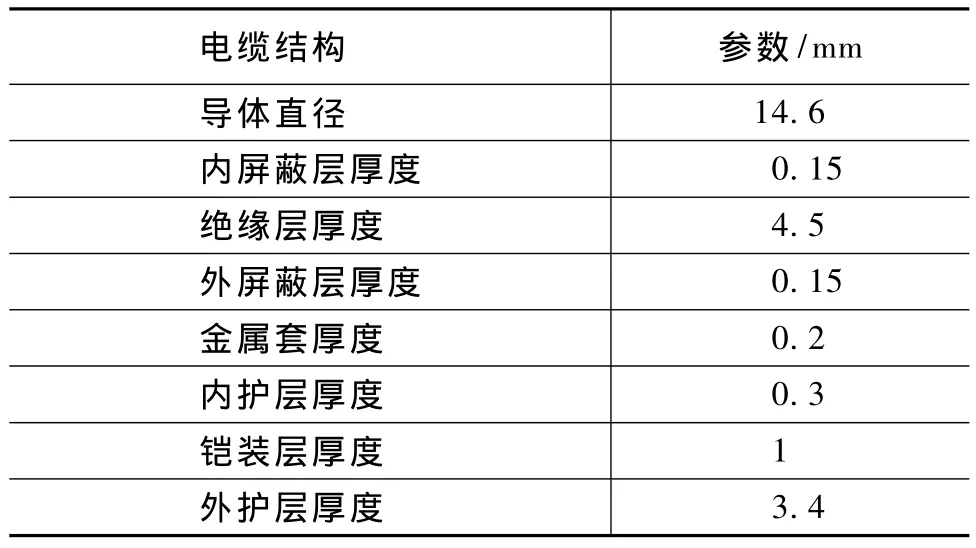
表1 電纜結(jié)構(gòu)參數(shù)Tab.1 Parameters of cable structure

表2 電纜敷設(shè)條件Tab.2 Installation condition of cable

圖4 電纜的有限元剖分模型Fig.4 FEM dissection model of cable

當電纜纜芯溫度迭代到90℃時，載流量為362.1A，試驗載流量為 365A［9］，誤差為 0.8% 。

當不考慮熱電耦合時，載流量為375.5A，與試驗載流量相比，誤差為2.9%。可見，考慮熱電耦合時載流量計算結(jié)果更接近試驗載流量。

當電纜周圍回填200mm厚的沙土，且沙土熱阻為2.0W·(m2·℃)時，電纜的載流量為319.2A。當三根同型號電纜平行排列敷設(shè)，電纜間距為200mm時，電纜的載流量為187A。當電纜周圍回填沙土時，三根電纜的載流量為167A。

5 結(jié)論

本文以土壤直埋的單根三芯電纜和三根三芯電纜平行排列為例，闡述了采用基于熱電耦合的有限單元法對電纜土壤直埋敷設(shè)時長時間運行的穩(wěn)態(tài)溫度場和載流量計算的方法。在電纜區(qū)域和土壤區(qū)域的剖分中用到了可變步長的離散化方法，能夠在不降低精確度的同時減少節(jié)點的數(shù)量。

采用數(shù)值計算方法確定載流量，可以方便地預測各種載流量時地下電纜的溫度值，確保電纜在安全溫度范圍內(nèi)工作，對電纜的敷設(shè)和運行都有一定的指導意義，應用前景非常廣闊。

［1］孔祥謙 (Kong Xiangqian).有限單元法在傳熱學中的應用(Application of finite element method in calorifics)［M］.北京:科學出版社 (Beijing:Science Press)，1998.

［2］Gela G，Dai J J.Calculation of thermal fields of underground cables using the boundary element method［J］.IEEE Trans.Power Delivery，1988，3(4):1341-1347.

［3］Hanna M A，Chikhani A Y，Salama M A A.Thermal analysis of power cables in multi-layered soil，practical consideration［J］.IEEE Trans.Power Delivery，1993，8(3):772-777.

［4］Hanna M A，Chikhani A Y，Salama M M A.Thermal analysis of power cables in multi-layered soil，part3:case of two cables in a trench［J］.IEEE Trans.Power Delivery，1993，8(3):572-577.

［5］Hanna M A，Chikhani A Y，Salama M M A.Thermal analysis of power cables in multi-layered soil［J］.IEEE Trans.Power Delivery，1993，8(3):761-771.

［6］梁永春，李彥明，柴進愛 (Liang Yongchun，Li Yanming，Chai Jinai).地下電纜群穩(wěn)態(tài)溫度場和載流量計算新方法 (A new method to calculate steady-state temperature field and ampacity of underground cable system)［J］.電工技術(shù)學報 (Trans.China Electrotechnical Society)，2007，22(8):185-190.

［7］梁永春，孟凡鳳，王正剛 (Liang Yongchun，Meng Fanfeng，Wang Zhenggang).電纜群鄰近效應的計算和優(yōu)化排列 (Proximity effect and optimized arrangement of cable bundles)［J］.電工電能新技術(shù) (Adv.Tech.of Elec.Eng.＆ Energy)，2006，25(2):39-41.

［8］梁永春，柴進愛，李彥明 (Liang Yongchun，Chai Jinai，Li Yanming).有限元法計算交聯(lián)電纜渦流損耗 (Calculation of eddy current losses in XLPE cables by FEM)［J］.高電壓技術(shù) (High Voltage Eng.)，2007，33(9):196-199.

［9］馬國棟 (Ma Guodong).電線電纜載流量(Ampacity of wire and cable)［M］.北京:中國電力出版社 (Beijing:China Elec.Power Press)，2003.5-29.