熱電發電裝置的動態模型及分析

袁義生，熊 晶

(華東交通大學電氣學院，江西 南昌330013)

1 引言

能源緊張及環境污染的加劇使得廢熱回收技術成為提高能源利用率的一個重要研究方向。以汽車為例，傳統汽車石油燃料產生的能量約30%轉換成機械能來驅動汽車行駛，另外約40%以廢氣方式排放，還有約30%在引擎冷卻過程中流失，其能源利用率極低［1-2］。因此，研究如何將這些廢熱回收利用是一項極其有益的研究工作。

熱電發電裝置由熱端導熱片、熱電發電器件和冷端散熱片構成，之后再經后級直流變換器將熱電發電器件發出的電能轉換后送給蓄電池儲存。

但熱電發電及變流裝置要得到廣泛應用，還有一些基礎性問題需要解決，其中重要一點就是熱電發電裝置的數學模型的建立。這是因為后級直流變流器的控制特性，包括做最大功率跟蹤和功率匹配［3］時的動態特性都與前級熱電發電裝置的動靜態模型密切相關。然而，現有的熱電發電器件的模型有兩種，一種是設計模型，另外一種是電等效模型。設計模型是基于器件物理特性而建立的微觀參數模型，主要為評估器件Seebeck效應建立，此類模型主要是不考慮器件工作條件的物理靜態模型［4］，也有少數考慮了外部工作條件的準動態模型［5］。電等效模型則是將熱電發電器件的輸出等效為電壓源U和內阻Rin串聯電路。此類模型可以由廠家給出特性參數。但問題是，器件廠家標示的器件參數是在器件兩端溫差ΔT和負載固定的靜態條件下測量得到的，并不反映熱電發電器件的動態特性，尤其是大信號特性。而且，熱電發電器件處于熱端尾氣管和冷端散熱器之間，這兩者的特性對熱電器件的輸出電壓動態特性都有影響;還有就是后級直流變換器的等效輸入電阻對熱電發電器件的輸出電壓也有影響。這些都是之前的研究沒有系統考慮的問題。

所以，本文建立熱端導熱片、熱電發電器件和冷端散熱器構成的完整熱電發電裝置的動態模型。分析熱電發電器件輸出電壓的熱源響應特性，以及輸出負載響應特性。建立等效仿真電路模型，并用小裝置試驗測試驗證了模型的正確性。

2 熱電發電裝置結構及原理

熱電發電裝置由熱端導熱片(散熱片)、熱電發電器件和冷端散熱器構成，如圖1所示。其中，因為熱電發電器件為雙層半導體串聯結構，表面不絕緣，所以在熱冷端散熱器與熱電發電器件之間還有絕緣陶瓷片。而虛線框的后級直流變換器部分可用一個等效負載電阻Ro來代替。

圖1 熱電發電裝置結構Fig.1 Structure of thermoelectric generator equipment

熱電發電器件Seebeck效應的輸出電壓表示為:

式中，α是 Seebeck系數;ΔT是熱電發電器件熱端和冷端間的溫差。α值由材料特性決定。但ΔT卻不僅取決于熱電發電器件的傳熱特性，由圖1可知也與熱源變化、冷熱端散熱片傳熱特性和等效負載電阻Ro有關。所以，建立完整的熱電發電裝置模型需要逐個建立上述部件數學模型并連接構成。

3 散熱片動態模型

對任意微小封閉容積，據熱力學第一定律［8］有:

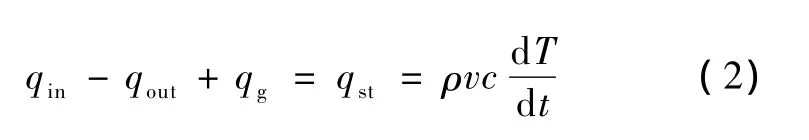
式中，ρ、v、c分別為此封閉容積的密度、體積、比熱容;q表示能量流動的速率，即熱流量。此式表示控制容積中的能量速率的增大，必定等于進入控制容積的能量速率，減去離開控制容積的能量速率，再加上在同一瞬間控制容積內產生熱量的速率。

由于導熱系數恒定，溫度沿厚度方向線性分布。如果散熱片很薄，可以使用兩端平均溫度代替散熱片溫度。定義其兩端溫度分別為T1和T2，則有:

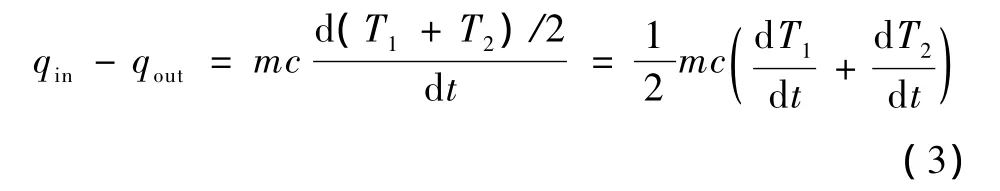
式中，m為封閉容積的質量。再結合基本的靜態熱阻定律:

式中，θ表示散熱片的熱阻。可以得到熱冷端散熱器完整的靜動態特性等效電路如圖2所示。

4 熱電發電器件的動態等效模型

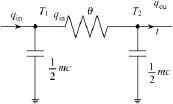
圖2 平板散熱器等效電路圖Fig.2 Equivalent model of flat heatsink

為了提高熱電轉換效率，熱電發電器件通常制作成平板狀。當熱電發電器件輸出接負載電阻Ro時，體內的熱能就轉換成電能，有:

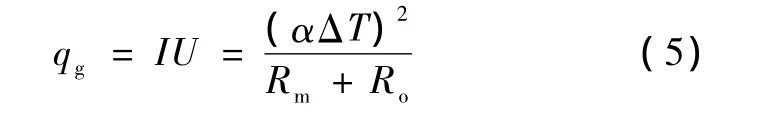
式中，Rm是熱電發電器件本身電阻。

對于半導體熱電模塊，考慮塞貝克效應及帕爾帖效應，單位時間內從熱接觸層吸收的熱量為:

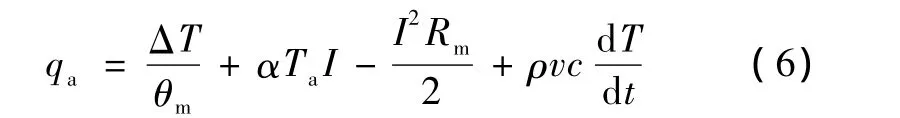
熱電器件單位時間內放給冷端接觸層的熱量為［9］:

式中，Ta和Tc分別為熱電模塊熱面和冷面的溫度;θm為熱電模塊的熱阻。并且:

根據熱力學第一定律可得:

可以建立熱電模塊的等效模型，如圖3所示。

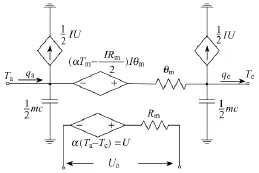
圖3 熱電發電器件等效模型Fig.3 Equivalent model of thermoelectric generator

5 完整模型及分析

5.1 完整模型

在上述分析的基礎上，據圖1裝置結構可以得到完整的熱電發電裝置的等效電路模型如圖4所示。

圖4 熱電發電裝置等效電路模型Fig.4 Equivalent circuit model of thermoelectric equipment

在圖4中，T1、T2分別為熱端和冷端溫度;θ1為熱端散熱片的熱阻;C1為熱端散熱片的熱容，其值為熱端散熱片的質量與比熱容的乘積的1/2;C3為熱電發電器件的熱容;θ4為冷端散熱片的總熱阻;C2為冷端散熱片的熱容;θ2和 θ3分別為熱端和冷端導熱陶瓷墊片熱阻和接觸熱阻之和;Rm和Ro分別為熱電發電器件的內阻和等效負載電阻。因為絕緣陶瓷片熱容小，因此圖中忽略。

5.2 模型分析

(1)源響應

源響應是指熱源波動對Seebeck輸出電壓的影響。假定熱源信號階躍變化，而熱電發電器件輸出開路，即在圖4中設定I=0，Ro斷開，就可以分析模型的源響應特性。這是一個多階的熱阻容θC慣性電路。熱電發電器件Seebeck效應輸出電壓U與ΔT(Ta－Tc)成正比。當 qin是一個初始為零的階躍函數時，ΔT的穩態值就等于qinθm，但其暫態分量則取決于各串聯的熱阻容乘積。在實際的系統中，熱端散熱片熱容大;熱電發電器件的熱容則最小;冷端散熱片的熱容較大。所以，ΔT的暫態分量主要取決于θ1C1和θ4C2兩個時間常數。即 Seebeck效應輸出電壓U的源階躍響應特性曲線是一個簡化的二階慣性環節。

(2)負載響應

負載響應是指等效負載電阻Ro(后級直流變換器電路等效輸入電阻)階躍變化時，Seebeck效應輸出電壓U的響應特性。此時可以假定熱源穩定。等效電路如圖5所示。

分析負載由開路(R=∞)階躍變化至 Ro時的輸出電壓響應。由于Ro和Rm的分壓，此時負載電壓Uo會瞬間降低。之后，因為IU/2的分流作用，流過 θm的熱量 qm下降;且(αTa－IRm/2)Iθm的存在，使得熱冷端溫差ΔT下降。所以，負載電壓Uo會繼續隨Seebeck電壓U下降而下降。由于熱電發電器件的效率很低，IU/2遠小于qa，所以負載電壓Uo繼續下降的過程中可以忽略熱端散熱器的影響qa不變。此時，負載電壓Uo基本按θmC3時間常數規律下降至穩定值。

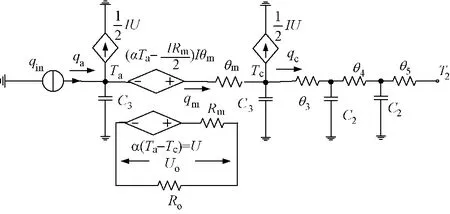
圖5 負載響應等效電路Fig.5 Equivalent circuit of load response

綜上所述，可以看出:熱電發電裝置輸出電壓的變化在其物理特性基礎上，不僅與熱源的改變，也與后級負載的變化有關。

6 仿真與實驗

在實驗室搭建了一個小型熱電發電裝置，其中的熱電發電器件采用了一片Hi-Z公司生產的HZ-14(可見該公司網站)，熱源采用熱風槍來模擬，冷端采用強迫風冷使冷端散熱器外側溫度與空氣溫度接近。

按照圖4在電路仿真軟件SABER中建立仿真電路模型。其中的溫度，熱阻和熱容分別用電壓，電阻和電容來代替。

系統各部分的熱阻和熱容按照文獻［8］中公式計算，熱電發電器件的熱阻在說明書中查。參數見表1。

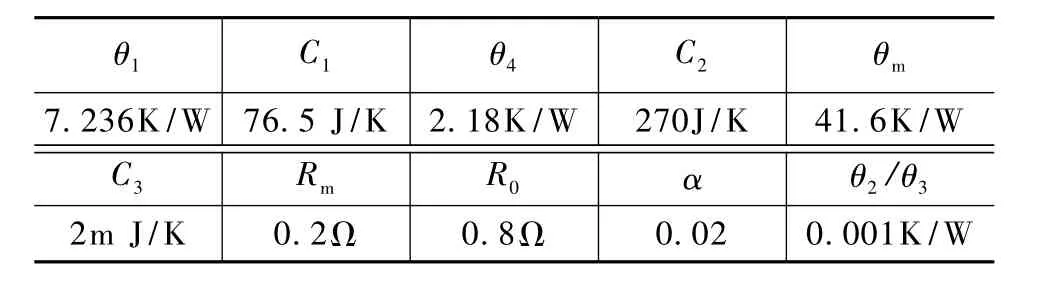
表1 仿真和試驗參數Tab.1 Parameters of simulation and experiment

實驗首先測試了裝置的負載響應特性。在熱源及溫度穩定的條件下，投卸等效輸出電阻 Ro，測試其輸出電壓響應特性。其中，圖6(a)和6(b)分別為投載下仿真和實驗的負載電壓Uo波形圖。圖7(a)和7(b)分別為卸載下仿真和實驗的負載電壓Uo波形圖。由圖可見，投載瞬間負載電壓Uo先迅速下降，而后沿曲線下降約5s后穩定。卸載時相反。實驗和仿真結果吻合。

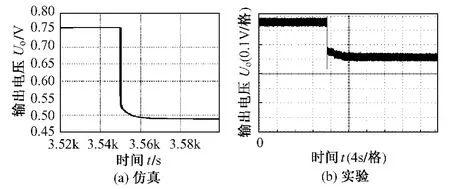
圖6 投載下Uo仿真和實驗波形Fig.6 Simulation and experimental waveforms ofvoltage Uoin load-on transient

圖7 卸載下Uo仿真和實驗波形Fig.7 Simulation and experimental waveforms of voltage Uoin load-off transient

其次測試了裝置的源響應特性。在熱源加熱溫度穩定后斷開熱源，分別考察空載和帶載情況下的負載電壓Uo響應。圖8(a)和8(b)分別是空載下仿真和實驗波形。圖9(a)和9(b)分別是帶載下仿真和實驗波形。可見，源響應負載電壓Uo下降時間達到1800s，遠遠超過負載響應時間，這與第4節的分析吻合。另外，帶載下的源響應速度略快于空載下的源響應速度，但并不顯著，這是因為熱電發電器件的效率低，輸出電功率遠小于傳遞的熱量。

圖8 空載下斷熱源時Uo仿真和實驗波形Fig.8 Simulation and experimental waveform of voltage Uoin hot source cut-off transient without load

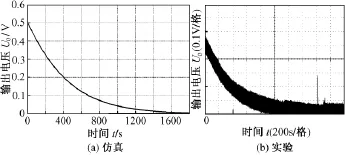
圖9 帶載下斷熱源時Uo仿真和實驗波形Fig.9 Simulation and experimental waveform of voltage Uoin hot source cut-off transient with load

7 結論

建立了熱電發電裝置的動態模型和等效電路模型，分析了其源響應和負載響應特性。指出了熱電發電器件的輸出電壓源響應是一個由散熱器決定的大時間慣性特性曲線，而負載響應則是由熱電發電器件決定的小時間慣性特性曲線。這對后級直流變換器主電路和控制電路的進一步研究具有重要參考價值。建立的小型實驗裝置的實驗和仿真結果吻合，證明了模型的有效性。

［1］Yang Jihui.Potential applications of thermoelectric waste heat recovery in the automotive industry［A］.2005 International Conference on Thermoelectronics［C］.New York，USA，Aug.2005.19-23.

［2］Yang Jihui.Development of thermoelectric technology for automotive waste heat recovery［R］.Washington:DOE USA，2008.

［3］Rae Young Kim，Jih-Sheng Lai.A seamless mode transfer maximum power point tracking controller for thermoelectric generator applications［J］.IEEE Trans.on Power Electronics，2008，23(5):2310-2317.

［4］宋瑞銀，李偉，楊燦軍，等 (Song Ruiyin，Li Wei，Yang Canjun，et al.).微小型熱電發電器建模及優化設計研究(Modeling and optimal design for mic-thermoelectric generator)［J］.太陽能學報 (Acta Energiae Solaris Sinica)，2006，27(6):554-558.

［5］Rasit Ahiske.New method for investigation of dynamic parameters of thermoelectric modules［J］.Electric Engin，2007，15(1):51-65.

［6］Simon Lineykin，Sam Ben-Yaakov.Modeling and analysis of thermoelectric modules［A］.IEEE APEC 2005［C］.New York，USA，2005.2019-2023.

［7］Chavez J，Ortega J，Salazar J，et al.Spice model of thermoelectric elements including thermal effects［A］.Proc.Instrumentation and Measurement Tech.Conference［C］.New York，USA，2000.1019-1023.

［8］Incropera F P，葛新石譯 (translated by Ge Xinshi).傳熱和傳質基本原理 (Fundamentals of heat and mass transfer)［M］.北京:化學工業出版社 (Beijing:Chemical and Industry Press)，2009.

［9］Omer S A，Infield D G.Design optimization of thermoelectric devices for solar power generation［J］.Solar Energy Materials and Solar Cells，1998，(53):67-82.