考慮線路有功傳輸約束的靜態電壓穩定分析

初 壯，王亮亮，蔡國偉

(東北電力大學電氣工程學院，吉林省 吉林市132012)

1 引言

隨著電力系統的不斷發展和擴大，為滿足不斷增長的負荷需求，電網在接近極限輸送能力狀態下運行，從而較大程度上威脅著電壓穩定。負荷增長和設備停運是導致電壓失穩的兩個主要原因。當負荷緩慢增長引起母線電壓緩慢下降，在逼近臨界點時系統運行人員可以采取相應的控制措施。當系統的負荷不斷增加，輸電系統承載不斷加重時，輸電線路停運將使系統的穩定域即刻收縮而導致電壓的突然失穩。

在電壓穩定研究方面，常利用一些指標來衡量電網的電壓穩定能力，它能讓運行人員了解當前系統離電壓臨界點還有多遠或者穩定裕度有多大，由于裕度指標具有線性度好、直觀、易于理解等優點，因此成為目前應用比較廣泛的電壓穩定性指標。在計算過程中，一般把當前系統與臨界點的距離用可額外傳輸的負荷功率來表示，稱之為負荷裕度。它的大小直接反應了當前系統承受負荷波動，維持電壓穩定的能力。求取系統電壓穩定臨界點的各種方法:有連續潮流法［1-2］、直接法［3-4］、基于最優潮流的方法［5］等。

非線性規劃法將電壓穩定臨界點的求取轉化為優化負荷問題［6］。文獻［7］在求取電壓穩定臨界點的過程中把有功電源上下限、無功電源上下限、節點電壓上下限作為不等式約束，并沒有考慮線路傳輸有功功率約束的影響。隨著負荷的不斷增加可能由于某條線路的輸電能力大小。在本文中把線路有功傳輸功率作為不等式約束加入到模型中，采用原對偶內點法［8-9］來求解，通過與不考慮線路有功傳輸約束時各支路的潮流進行對比分析，找到其中的薄弱支路。文中最后比較和分析了這兩種情況下求得的系統臨界值的差異。

2 考慮線路有功約束的負荷裕度模型

以運行點位于靜態安全域為電壓穩定判據，求解系統的負荷裕度模型為

等式約束為擴展潮流方程:

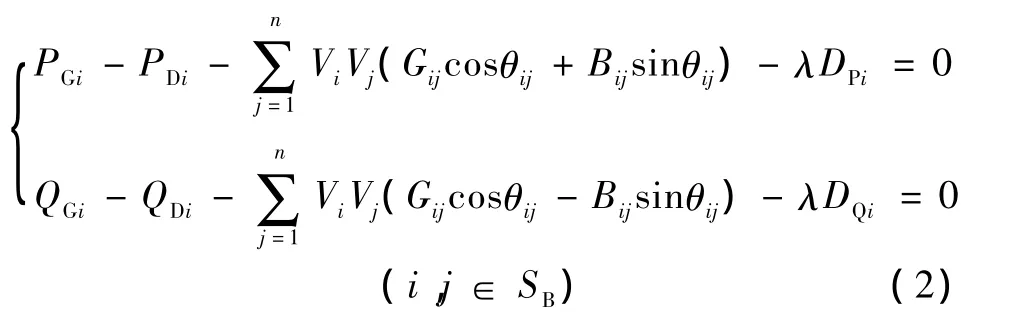
不等式約束為系統靜態安全運行約束:

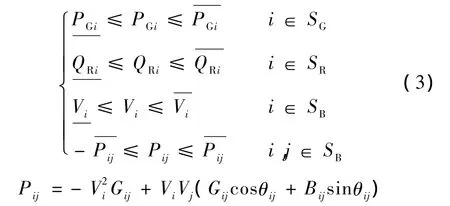
式中，SB為所有節點的集合;SG為有功電源的集合;SR為無功電源的集合;θij為節點 i與節點 j之間的相角差;Gij、Bij分別為導納矩陣元素的實、虛部;i=1，2…N;N 為節點數;PDi、QDi分別為節點 i上的負荷有功和無功功率;不等式約束中 PGi、QRi、Vi、Pij分別為有功發電、無功發電、節點電壓、線路ij的傳輸有功功率;上標“—”表示上限值;下標“—”表示下限值;λ∈R1為標量，反應負荷水平的參數;DPi=［DP1，…，DPn］T、DQi=［DQ1，…，DQn］T為負荷的增長方向。

3 原始-對偶內點法求解

3.1 原始-對偶內點法

非線性原對偶內點法將對數壁壘函數與牛頓法結合起來應用到非線性規劃問題，該方法收斂迅速，魯棒性強，對初值的選擇不敏感，在求解電力系統優化問題中已得到廣泛的應用。

將式(1)～式(3)轉化為如下模型求解:

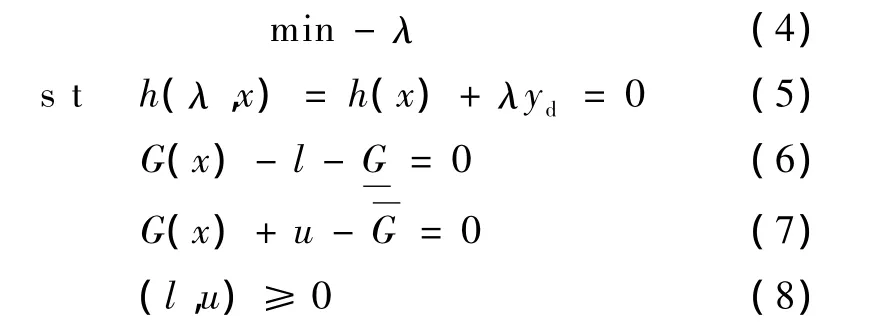
式中，(l，u)∈Rr為松弛變量;x∈Rn為狀態變量;λ=0對應初始運行點。

利用拉格朗日方法將約束優化問題轉化為無約束優化問題，形成拉格朗日函數:

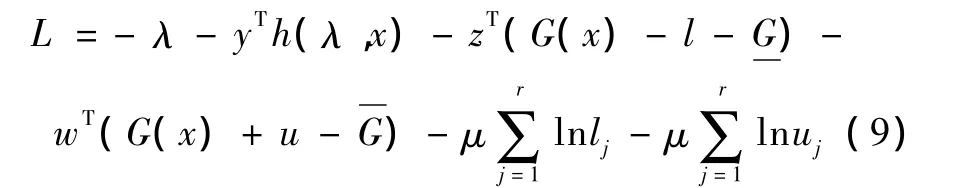
式中，y=［y1，…，ym］，z=［z1，…，zr］，w=［w1，…，wr］均為拉格朗日乘子。該問題極小值存在的必要條件是拉格朗日函數對所有變量及乘子的偏倒數為0，得到以下非線性方程:

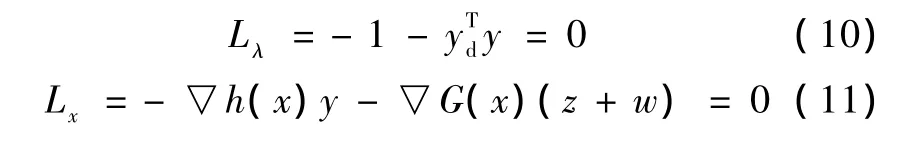
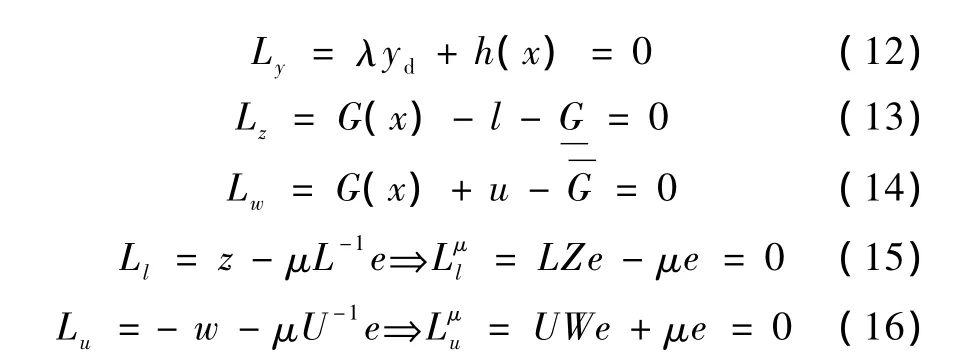
式中，L=diag(l1，…，lr)，U=diag(u1，…，ur)，W=diag(w1，…，wr)，Z=diag(z1，…，zr)，e=［1，…，1］T∈Rr。定義Gap=lTz-uTw，稱為互補間隙。

然后用牛頓法求解式(10)～式(16)，得到修正方程即可，詳細的求解過程參考文獻［7］。

原始-對偶空間中最大步長按下式確定:

3.2 原始-對偶內點法流程

原對偶內點法計算負荷裕度的流程圖如圖1所示。其中初始化部分包括:

(1)設優化問題各變量的初值;

圖1 原始-對偶內點法流程框圖Fig.1 Flow chart of primal-dual interior point method

(2)設置松弛變量 l、u.，保證［l，u］T＞0;

(3)設置拉格朗日乘子 z、w、y，使它們滿足［z＞0，w ＜0，y≠0］T;

(4)取中心參數 σ∈(0，1)，給定計算精度 ε=10-6，迭代初值k=0，最大迭代次數kmax=50。

4 算例分析

本文以 IEEE-30節點系統進行仿真，圖2是IEEE-30節點系統的接線圖，數據采集來自文獻［10］，基準功率為100 MW。在進行計算的過程中負荷采用原功率因數增長。把系統分為兩種情況來比較:一種是不考慮線路有功潮流安全約束;另一種是把線路有功潮流約束考慮進去。線路有功邊界是指線路可以傳輸有功的最大值。

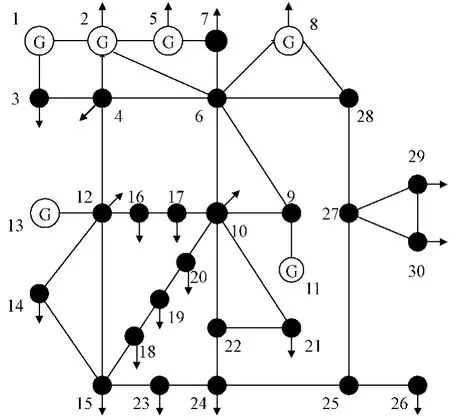
圖2 IEEE-30節點系統接線圖Fig.2 Wiring diagram of IEEE-30 bus system

隨著模擬負荷的不斷增加，當不考慮線路有功傳輸約束時有15條支路的有功潮流出現越界，這些越界的支路是系統的薄弱支路。表1是這15條支路功率在第一種情況下出現的最大功率值。

從表1可以看出:不考慮線路有功傳輸約束時，這15條薄弱支路出現有功潮流越界，最大值均超過了線路的最大傳輸能力。圖3和圖4分別是薄弱支路7和28在兩種情況下的有功功率迭代分布圖。

從圖3和圖4可以看出:不考慮線路有功傳輸約束時，隨著負荷的不斷增加，線路4-6和線路22-24的有功功率變化幅度比較大，而且最大值均越過它們的邊界范圍;考慮線路有功傳輸約束時，隨著負荷的增加，線路上的有功功率變化比較平穩，都在線路可以傳輸功率的范圍之內。

表2是系統在臨界處的有功及無功值。在第二種情況下求得的系統臨界值要比第一種情況小，由于在第二種情況下不等式組的解集要比第一種情況下的小。考慮線路有功傳輸約束時，求得的結果更準確，便于系統運行人員更準確地了解系統運行狀態，防止電壓失穩事故的發生。在第二種情況下的迭代次數要比第一種情況大，這是由于在計算過程中考慮線路有功傳輸約束，求解過程中需要的迭代步長較小，在尋優過程中需要更多的迭代次數來滿足約束條件下的解。所以在進行靜態電壓穩定分析時應該考慮線路有功傳輸約束的影響。

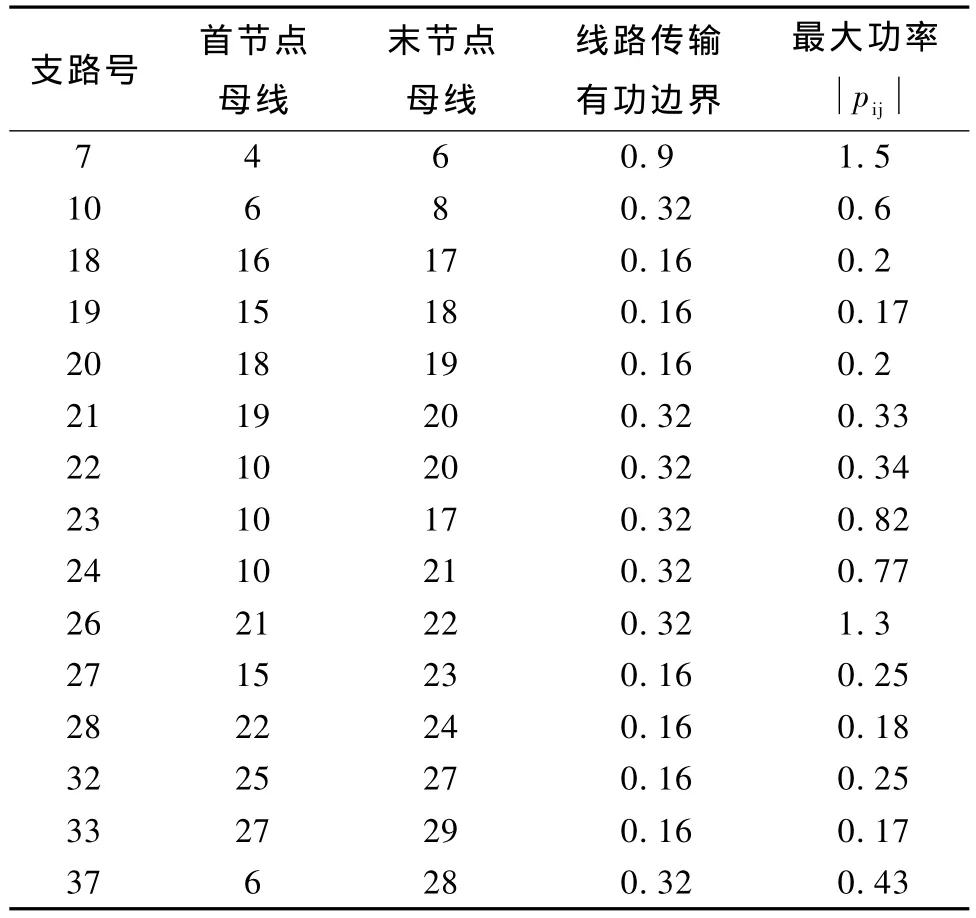
表1 薄弱支路Tab.1 Weak branch of system

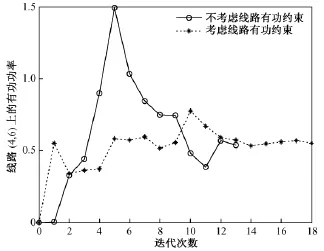
圖3 線路4-6的有功功率Fig.3 Active Power of transmission line 4-6

圖4 線路22-24的有功功率Fig.4 Active power of transmission line 22-24

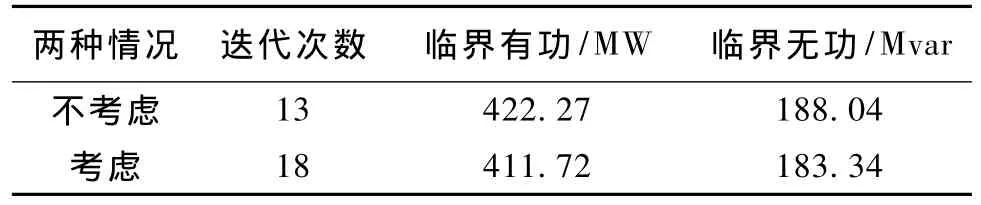
表2 臨界點系統的有功及無功Tab.2 Active power and reactive power at critical point of system

5 結論

本文在求解電壓穩定臨界點的過程中，把線路有功傳輸功率約束加入到不等式中。通過對比兩種情況下支路潮流的分布曲線可以識別其中的薄弱支路，系統調度運行人員能更好地監視系統的各支路潮流。通過數值仿真，驗證了本模型的正確性和有效性，更符合實際要求。本方法可為電力系統的規劃及運行人員提供系統的負荷裕度，這對系統的安全可靠性具有非常重要的指導意義。

［1］Chiang Hsiao Dong，Flueck A J，Shah K S，et al.A practical tool for tracing power system steady-state stationary behavior due to load and generation variations［J］.IEEE Trans.on Power Systems，1995，10(2):623-634.

［2］胡彩娥(Hu Caie).應用基于連續潮流算法的遺傳算法進行靜態電壓穩定分析 (Application of continuous power flow based genetic algorithm to analysis of static voltage stability)［J］.電網技術(Power System Technology)，2004，28(15):57-61.

［3］郭瑞鵬，韓禎祥(Guo Ruipeng，Han Zhenxiang).計算最近電壓崩潰臨界點的實用算法(A practical algorithm for calculating the closest point of collapse)［J］.電網技術(Power System Technology)，2006，30(3):13-17.

［4］Ca?izares C A，Alvarado F L，Demarco C L，et al.Point of collapse methods applied to AC-DC power systems［J］.IEEE Trans.on Power Systems，1992，7(2):673-683.

［5］Irisarri G D，Wang X，Tong J，et al.Maximum load ability of power systems using interior point nonlinear optimization method ［J］.IEEE Trans.on Power Systems，1997，12(1):162-172.

［6］郭瑞鵬，韓禎祥，王勤(Guo Ruipeng，Han Zhenxiang，Wang Qin).電壓崩潰臨界點的非線性規劃模型及算法(Nonlinear programming model＆algorithm for point of collapse)［J］.中國電機工程學報(Proceedings of the CSEE)，1999，19(4):14-17.

［7］韋化，丁曉鶯(Wei Hua，Ding Xiaoying).基于現代內點理論的電壓穩定臨界點算法(An algorithm for determining voltage stability critical point based on interior point theory)［J］.中國電機工程學報(Proceedings of the CSEE)，2002，22(3):27-31.

［8］邱曉燕，史繼莉(Qiu Xiaoyan，Shi Jili).基于內點法的電力系統最大輸電能力計算(Power system total transfer capacity calculation based on interior point method)［J］.高電壓技術(High Voltage Engineering)，2006，32(6):101-104.

［9］Jazayeri P，Shoarinejad A，Rosehart W.電力穩定約束的最優潮流(Voltage stability constrained optimal power flow)［J］.電力系統自動化(Automation of Electric Power Systems)，2005，29(16):48-55.

［10］吳際舜(Wu Jishun).電力系統潮流計算的計算機方法(Computer methods for power flow problems of power system)［M］.上海:上海交通大學出版社(Shanghai:Shanghai Jiaotong University Press)，2000.