可靠度的雙側M-Bayes可信限

韓明

(福建工程學院數理系,福建 福州 350108)

可靠度的雙側M-Bayes可信限

韓明

(福建工程學院數理系,福建 福州 350108)

對二項分布的可靠度,提出了一種新的參數估計方法—雙側M-Bayes可信限法.在無失效數據情形,給出了可靠度的雙側M-Bayes可信的定義、雙側M-Bayes可信的估計,關于雙側M-Bayes可信限的性質提出了一個猜想—可靠度的雙側M-Bayes可信限與雙側經典置信限的關系.最后,給出了一個例子,通過這個例子可以看出雙側M-Bayes可信限優于雙側經典置信限.

可靠度;無失效數據;雙側M-Bayes可信限;雙側經典置信限

1 引言

在有些情況下,很難確定產品的壽命分布類型,有時雖然產品的壽命分布類型已知,但獲得的數據僅僅是失效個數,而無精確的失效時間,這時可以借助非參數方法來獲得可靠度的估計.設某產品的壽命分布類型是未知的,現從中隨機抽取n個樣品進行定時截尾試驗,若在截尾時間段內有X個樣品失效,又產品的失效與否是互相獨立的,則X是一個服從二項分布的隨機變量,于是有

其中0＜R＜1,R為產品的可靠度.

這樣研究可靠度的非參數估計問題,就轉化為研究二項分布(1)式中參數R的估計問題.

隨著科學技術的發展,產品的可靠性不斷提高,高可靠性產品在定時截尾可靠性試驗中經常出現無失效數據.無失效數據問題的研究,對于建立在失效數據基礎上的現有可靠性理論來說,是一個有一定難度的問題.自文獻[1]發表以來,對無失效數據問題的研究逐漸引起了國內外的重視,并且已取得了一些成果[23].

關于參數估計,近年來用Bayes方法取得了一些進展.特別是在文獻[4]中提出了多層先驗分布的想法以來,Bayes方法和多層Bayes方法在無失效數據的處理上取得了一些進展.在文獻[5]中,對二項分布,給出了一種Bayes估計.在文獻[6]中,對二項分布無失效數據情形,給出了可靠度的多層Bayes估計.在文獻[7]中,對產品的可靠度提出了一種新的參數估計方法—“單側M-Bayes可信限法”,給出了單側M-Bayes可信下限的定義和單側M-Bayes可信下限的估計公式,并指出單側M-Bayes可信下限優于單側經典置信下限.

本文在文獻[7]的基礎上提出了一種新的參數估計方法—雙側M-Bayes可信限法.在第二節中,給出了可靠度的雙側M-Bayes可信下限的定義、雙側M-Bayes可信上限的定義;在第三節中,給出了可靠度的雙側M-Bayes可信下限的估計、雙側M-Bayes可信上限的估計;在第四節中,提出了雙側M-Bayes可信限的猜想—可靠度的雙側M-Bayes可信限與雙側經典置信限的關系;在第五節中,給出了數值算例.

2 雙側M-Bayes可信限的定義

若R的先驗分布為截尾冪分布,其密度函數為

在文獻[7]中給出了可靠度的單側M-Bayes可信下限的定義,以下在文獻[7]的基礎上將給出可靠度的雙側M-Bayes可信下限、雙側M-Bayes可信上限的定義.

2.1 雙側M-Bayes可信下限的定義

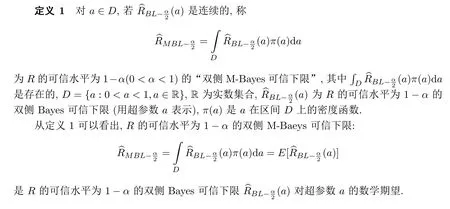
2.2 雙側M-Bayes可信上限的定義

3 雙側M-Bayes可信限的估計

以下分別給出雙側M-Bayes可信下限的估計、雙側M-Bayes可信上限的估計.

3.1 雙側M-Bayes可信下限的估計

3.2 雙側M-Bayes可信上限的估計

4 雙側M-Bayes可信限的性質

以下將給出可靠度的雙側M-Bayes可信限與相應的雙側經典置信限的關系.

4.1 雙側經典置信限

4.2 雙側M-Bayes可信限與雙側經典置信限的關系

在定理1和定理2中,分別給出了可靠度的雙側M-Bayes可信下限的估計和雙側M-Bayes可信上限的估計;在定理3中,給出了可靠度的雙側經典置信下限的估計和雙側經典置信上限的估計.那么雙側M-Bayes可信限與雙側經典置信限之間有什么關系呢?以下將給出的猜想將回答這個問題.

5 數值算例

表1 dMB1,dMB2和dC的計算結果(n=5)

表2 dMB1,dMB2和dC的計算結果(n=10)

表3 dMB1,dMB2和dC的計算結果(n=20)

表4 dMB1,dMB2和dC的計算結果(n=50)

表5 dMB1,dMB2和dC的計算結果(n=100)

圖1 n=5情形

圖2 n=10情形

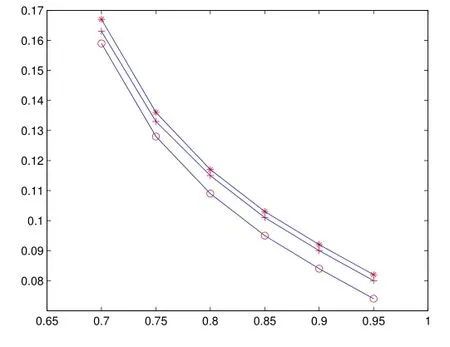
圖3 n=20情形

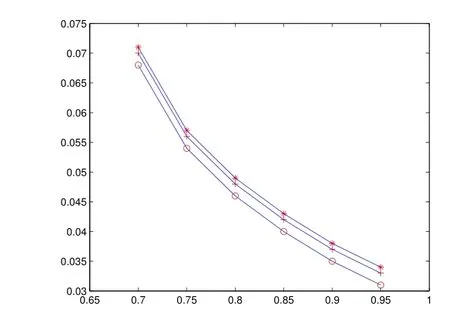
圖4 n=50情形

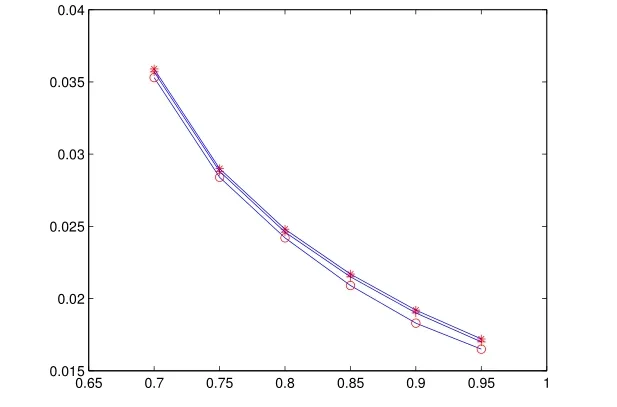
圖5 n=100情形

6 結束語

本文在文獻[7]的基礎上,提出了一種新的參數估計方法—–雙側M-Bayes可信限法.給出了可靠度的雙側M-Bayes可信的定義、雙側M-Bayes可信的估計,并提出了一個猜想—–可靠度的雙側M-Bayes可信限與雙側經典置信限的關系.

從數值算例以看出,對于同一可信(或置信)水平,有 dMB1＜dMB2＜dC,因此 dMB1, dMB2和dC滿足猜想.從數值算例還可以看出,本文提出的方法可行且便于應用.

[1]Martz H F,Waller R A.A Bayesian zero-failure(BAZE)reliability demonstration testing procedure[J]. Journal of Quality Technology,1979,11(3):128-137.

[2]韓明.無失效數據可靠性進展[J].數學進展,2002,31(1):7-19.

[3]韓明.基于無失效數據的可靠性參數估計[M].北京:中國統計出版社,2005.

[4]Lindley D V,Smith A F M.Bayes estimaters for the linear model[J].Journal of the Royal Statistical Society, Series B,1972,34:1-41.

[5]Miller K W,Morell L J,Noonan R E,et al.Estimating the probability of failure when testing reveals no failures[J].IEEE Trans.on Software Engineering,1992,18(1):33-43.

[6]韓明.Estimation of reliability based on zero-failure data[J].純粹數學與應用數學,2002,18(2):165-169.

[7]唐燕貞,韓明.可靠度的M-Bayes可信限[J].純粹數學與應用數學,2009,25(3):521-525.

[8]韓明,趙仁杰.成敗型無失效數據的可靠性分析[J].信息工程學院學報,1992,11(3):27-35.

The two-sided M-Bayesian credible limits of the reliability

Han Ming
(Department of Mathematics and Physics,Fujian University of Technology,Fuzhou 350108,China)

This paper introduces a new parameter estimation method,named two-sided M-Bayesian credible limits method,to estimate reliability derived from binomial distribution.In the case of zero-failure data, the de fi nition and estimation formulas of two-sided M-Bayesian credible limits are provided,moreover,about properties of two-sided M-Bayesian credible limits,author a guess is provided–relations among two-sided MBayesian credible limits and corresponding two-sided classical con fi dence limits.Finally,a example is given, through the example show that two-sided M-Bayesian credible limits is superior to the corresponding two-sided classical con fi dence limits.

reliability,zero-failure data,two-sided M-Bayesian credible limits, two-sided classics con fi dence limits

O213.2

A

1008-5513(2012)01-0001-07

2011-03-14.

福建省自然科學基金(2009J01001).

韓明(1961-),博士,教授,研究方向：數理統計與可靠性理論.

2010 MSC:62N05,62F15