輪轂孔雙鍵槽對稱度誤差測量方法研究

屈 波QU Bo

（重慶工業職業技術學院，重慶 401120）

0 引言

在工程機械中，如大型水泵、大功率減速機，其工作的額定功率較大，其輸出軸若使用單鍵來傳遞扭矩，鍵聯接的強度往往不夠，若用花鍵來傳遞功率，雖可滿足強度要求，但花鍵的制造成本較高，所以工程設計中常使用雙鍵聯接來傳遞較大的功率，是一種性價比較高的選擇。在雙鍵聯接中，對雙鍵鍵槽的對稱度要求較高，如果鍵槽對稱度的精度要求無法保證，將滿足不了承載能力的需求，所以必須完善實際生產中雙鍵對稱度誤差的測量方法問題。

1 輪轂孔雙鍵鍵槽對稱度其公差帶特征分析

一般情況下，軸轂聯接在采用雙鍵傳遞動力時，兩鍵在圓周方向必須是均布的，即2個鍵的中心平面的理想夾角為180°，圖1是輪轂孔雙鍵槽對稱度的圖紙標注示例。

圖1 輪轂孔雙鍵對稱度公差要求的圖紙標注

在此圖紙標注中，對2個鍵槽都標注了相對于基準軸線的對稱度要求，表面上看這是分別對2個鍵槽的中心平面提出的對稱度要求，但實際上對稱度公差要求從本質上說是一種位置公差要求，只不過此時2個被測鍵槽的中心平面的理想要素應是通過基準軸線的一個公共理想平面（筆者認為：這種公差要求如用位置度來標注能更準確地表達設計意圖），雙鍵鍵槽對稱度的公差帶應是以理想軸線為中心要素，對稱布置在此中心要素兩側的2個理想平面之間的區域，如圖2所示，兩理想平面之間的距離為對稱度公差值（圖中公差值為0.04 mm）。此類公差帶的位置有確定的一面，即此公差帶的中心平面必須通過基準軸線，但同時，這種公差帶也可以浮動，即評定鍵槽對稱度誤差值時，此公差帶可繞其基準軸線轉動，只要被測的2個鍵槽的中心平面位于此公差帶內，則這2個鍵槽的對稱度誤差就符合對稱度公差要求，工件此項檢測就是合格的。在實際測量與評定此類雙鍵鍵槽的對稱度誤差時，應使用定位最小包容區域來評定，其幾何特性與上述對稱度公差帶的幾何特性基本相同，不同的是此定位最小包容區域必須緊緊包容被測鍵槽的實際中心平面且具有最小的寬度，而此定位最小包容區域的寬度即為被測雙鍵鍵槽的對稱度誤差值。

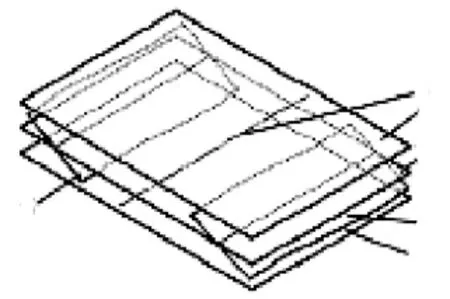
1.公差帶邊界平面；2.鍵槽Ⅱ的中心平面；3.公差帶的對稱中心平面；4.公差帶的基準軸線；5.鍵槽Ⅰ的中心平面圖2 輪轂孔雙鍵鍵槽對稱度公差帶示意圖

2 輪轂孔雙鍵鍵槽對稱度誤差測量方法

2.1 采用的測量裝置及需要測出的尺寸數據

如圖3、圖4 所示。在檢驗平板上放置一個帶夾緊裝置的V形架，準備一個與被測工件內孔直徑尺寸相同的檢驗心軸安裝在V形架的V形槽中，用壓緊裝置將其適當固定，將被測工件通過其內孔安裝在上述檢驗心軸上，要求配合間隙最好為零，實際配合面占孔面總長的一半即可，其目的是要露出需要檢測的雙鍵鍵槽。然后分別組合出2組量塊，量塊組的尺寸分別要根據兩鍵槽的實際尺寸j1、j2進行組合，并將這2組量塊與被測鍵槽無間隙地裝配在一起，再將一帶表架的千分表放置在檢驗平板上，用此千分表找正工件，使安裝在鍵槽中的量塊組工作面平行于檢驗工作臺工作面。在一般此類輪轂孔雙鍵鍵槽加工中，鍵槽的分度并不是通過分度頭進行的，而是在加工好一個鍵槽后，通過直接拆下插刀刀頭，將其翻轉180°后再次插入刀桿中夾緊，即可開始第2個鍵槽的加工，所以加工好的兩鍵鍵槽的中心平面一般是平行的，上述工藝方法是可以保證這一點的。所以在檢測中一般可同時將安裝在鍵槽中的量塊組工作面找正，使之平行于檢驗工作臺工作面。

然后，運用相對測量法的原理，用量塊校對好千分表，分別測出安裝在鍵槽中的2組量塊的上工作面到檢驗平板工作面的實際距離尺寸h1、h2，以及心軸相對于平板的最高素線到檢驗平板工作面的實際距離尺寸h3，再用內徑千分表測出工件內孔的實際直徑尺寸Da。

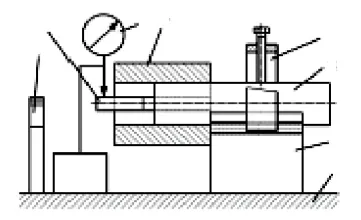
1.檢驗平板；2.V形架；3.心軸；4.V形架緊固裝置；5.工件；6.千分表；7.量塊；8.千分表調零量塊組圖3 測量裝置示意圖的主視圖

2.2 數據處理及對稱度誤差的計算

工件輪轂孔軸線到檢驗平板工作面的實際距離hx= h3－Da/2

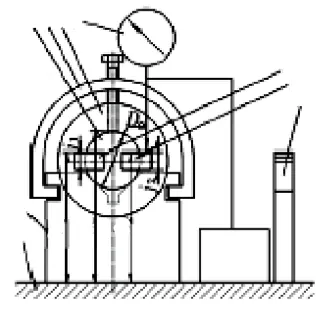
1.檢驗平板；2.V形架；3.心軸；4.V形架緊固裝置；5.工件；6.千分表；7.Ⅰ號量塊；8.Ⅱ號量塊；9.千分表調零量塊組圖4 測量裝置示意圖的左視圖

Ⅰ號量塊中心平面到輪轂孔軸線的實際距離

b = h1－j1/2－hx

Ⅱ號量塊中心平面到輪轂孔軸線的實際距離

a = h2－j2/2－hx

當計算得到的a值和b值符號相反時，說明兩被測鍵槽的中心平面分別位于基準軸線所在的水平面的異側，如圖5所示。圖中FM 線代表Ⅰ號量塊的中心平面，NH線代表Ⅱ號量塊的中心平面，這些平面分別模擬了兩個被測鍵槽的實際中心平面，下面要進行對稱度誤差的評定，但這里涉及到一個定位最小包容區域的判別問題，需要說明：國家標準中，并未給出定位最小區域的判別法，但可以根據最小包容區域的定義做出判別，而且本文所針對的此類對稱度誤差的最小包容區域有一些特殊性，首先，這種對稱度誤差的最小包容區域相對于基準是對稱的，其次，這類對稱度誤差最小包容區域的中心要素是一條基準軸線，即此類對稱度公差是所謂面對線的對稱度公差。

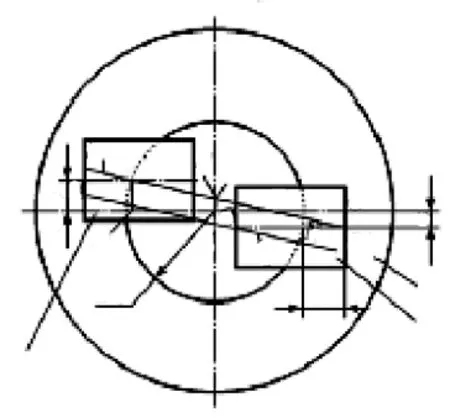
1.Ⅰ號量塊；2.Ⅱ號量塊；3.工件圖5 輪轂孔雙鍵鍵槽對稱度誤差分析與計算示意圖

所以根據上述特點，如圖5所示，因圖中的最小包容區域的基準軸線的投影具有投影積聚性，其投影成為一點O，過O點的最小包容區域的中心平面將評定對稱度誤差的最小包容區域分為對稱的兩半， 因此只要在此最小包容區域的一半區間內，點O與2個被測要素按評定直線度誤差的相間準則構成局部的最小包容區域，再以此為基礎得出的整個最小包容區域的寬度就應該是最小的。

根據上述分析，可在圖5中畫直線l1l2，使之過FM平面的點F和NH平面的點H，點O與點F和點H就構成高、低、高相間的狀態，即可構成局部的最小包容區域， 但這只是半個定位最小包容區域，然后再畫直線l2，使之平行于直線l1，并使直線l2到O 點的距離等于直線l1l2到點O 的距離，因此圖5 中上下2 條傾斜的直線l1、l2之間的區域就是評定對稱度誤差的定位最小包容區域。當然，除此之外還有一種畫l1的可能，就是過點N和點M畫線，點N和點M 和點O構成高、低、高相間的狀態，但很明顯由此形成的包容區域并不能完全包容被測鍵槽的實際中心平面，故不能采用。

所以，評定對稱度誤差的定位最小包容區域應如圖5所示，直線l1、l2代表包容被測鍵槽實際中心平面的極限包容面，豎直中心線與直線l1的交點為點P，過圓心點O的EK線為此定位最小包容區域的寬度，因此只要求出EK 線的長度即可求得此種情況下兩鍵槽的對稱度誤差，但圖中EK線的長度求解比較困難，而實際測量時直線l1傾斜角一般很小，在簡化計算而又能保持一定的測量精度前提下，可得OE≈OP，EK 線的長度約等于2倍的OP，而OP線的長度可按下面的方法求出：

因為△FDC ∽△HGC ∽△OPC

有

而FD＝b、GH=a

所以式（1） 變為

則OP=a OC/GC

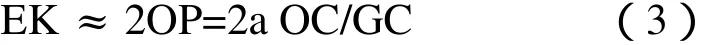
又從圖5 中的幾何關系可知OC+GC=R+h

則

將式（4）代入式（3），則

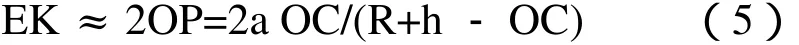
再從圖5 中的幾何關系可知DC≈OC+R而根據式（1）可知DC=b GC/a

所以可得b

再將式（ 4）代入式（6） ，可得

再將式（7）代入式（5），可得

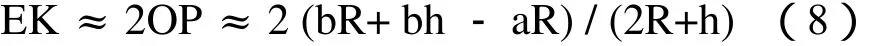
所以，最后式（8）變為

由于上述推導過程中沒有考慮各參數的正負號，考慮到可能出現|b|＜|a|的情況，為使公式更具普遍適用性，式（9）可變為

3 結束語

1）本文論述了在使用通用計量器具的條件下檢驗輪轂孔雙鍵鍵槽對稱度誤差的方法，并給出了具體情況下計算其對稱度誤差值的理論公式， 在工程實踐中對此類零件的相關檢測具有一定的指導作用。

2）本測量方法推導時忽略了鍵槽長度方向的位置誤差對對稱度誤差的影響，這是因為此種誤差易被工藝控制，一般來說誤差值極小。

3）本方法在測量開始階段，必須調整、找平工件的鍵槽中心平面，較耗費時間，也需要一定的技能，所以一般較適合首檢或小批生產的場合。

[1] 趙小明, 張武坤. 雙鍵對稱度誤差的測量與計算[J]. 現代制造工程, 2005(2): 107-108.

[2] 劉慶勝, 趙文廣. 國家標準中的軸鍵槽對稱度誤差計算公式的推導[J]. 工具技術, 2008(11): 107-109.

[3] 弓立明. 軋輥雙鍵槽對稱度的測量[J]. 工具技術,2003(9): 61.