基于偏差流的多工位裝配順序優化研究
石 煒,宋政立,王建國,張文興
(內蒙古科技大學 機械工程學院,包頭 014010)
0 引言
偏差流建模理論主要有:基于幾何運動學偏差分析,如極值法,蒙特卡洛法等,該類模型難以應用到復雜的零件裝配過程;基于有限元的偏差分析,如Liu提出的一維偏置梁單元模型和力學偏差仿真模型[1]、GM公司Hsieh的偏差優化模型[2]等,該類模型主要著眼于兩零部件的偏差協調分析,不能從裝配全過程角度描述偏差傳遞,難以體現偏差的傳遞和過程分配中的錯綜復雜關系;基于統計模型的偏差分析,如加拿大Wateloo大學的Lawless和Mackay等[3]的一階自回歸模型,該類模型是事后處理,依賴大量數據訓練學習;基于狀態方程的偏差分析,Jin和Shi[4]提出的狀態空間模型,該模型是基于機理的建模,能夠反映偏差在多工位間以流動的形式積累、耦合最終形成產品的過程,能夠應用到復雜的多工位裝配過程。
應用偏差流狀態空間模型可以對多工位裝配過程仿真,預測偏差。狀態空間模型的可觀性分析可以應用于偏差源診斷和測點布置等研究[5];狀態空間模型的可控性分析可以應用于夾具優化設計和公差綜合等研究[5]。在偏差流狀態空間模型基礎上,提出裝配順序矩陣,實現對過程信息的數學矩陣化處理,建立多工位裝配參數化狀態空間模型。以裝配順序矩陣和狀態空間模型為工具,優化裝配路線,降低產品尺寸偏差,提高產品質量。
1 多工位裝配偏差流狀態空間模型
多工位裝配過程包含大量的過程工藝信息,它們對最終產品質量影響巨大。提煉過程工藝信息,建立基于偏差流的狀態空間模型,可以對多工位裝配過程進行仿真并預測產品尺寸偏差。
多工位裝配過程是指產品由多個零件經過多個工位裝配而成,如圖1所示的裝配過程共有N個工位,在工位k,前k-1個工位上形成的零件稱為總成件,新零件與總成件裝配在一起形成工位k+1的總成件。依此類推最終形成產品。在工位k,零件偏差不但與本工位有關,而且與之前k-1個工位累積偏差有關。偏差在工位間累積、耦合,最終形成產品的偏差狀態。偏差主要來源于4個方面:1)當前工位的夾具定位偏差,如圖1中Uk;2)前序工位的累積偏差,如圖1中Xk-1;3)更換夾具引起的重定位誤差;4)裝配中的噪聲干擾,如圖 1 中 Wk。
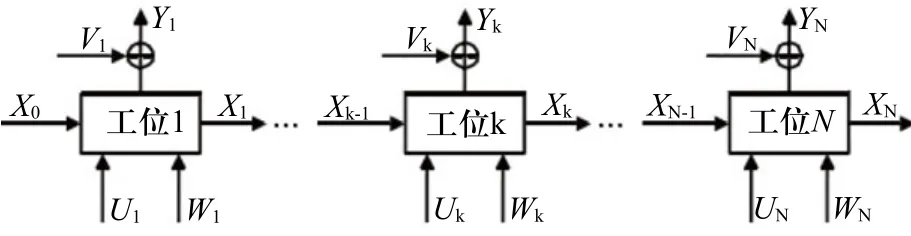
圖1 多工位裝配過程流程圖
多工位裝配過程相當于線性時變多輸入多輸出的離散系統,其狀態空間模型[6,7]為:
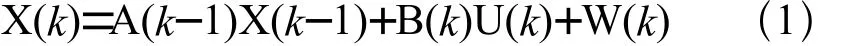
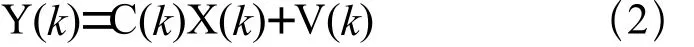
式(1)是狀態方程,式(2)是輸出方程,其中k是工位序號,A是n×n矩陣,n為狀態變量個數,稱為系統矩陣,反映前序工位累積偏差和重定位偏差對本工位偏差狀態的影響;B是n×m矩陣,m為輸入變量個數,稱為輸入矩陣,反映當前工位夾具定位偏差對本工位偏差狀態的影響;C是r×n矩陣,r為輸出變量個數,稱為輸出矩陣,反映零件上測點和參考點的相對關系。當前工位不進行測量時,C(k)為零矩陣;W,V為裝配和測量過程中的噪聲干擾。
將狀態空間模型式(1),式(2)合并,忽略零件裝配前的偏差,可得:
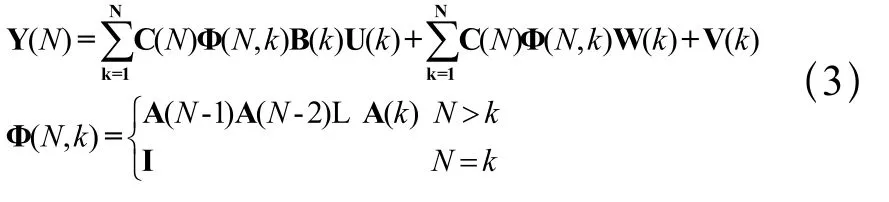
式(3)中Y(N)矩陣形式為:

式(4)可以簡寫成:

式(5)中U是輸入變量,Γ是模型矩陣,γ為裝配和測量時的噪聲干擾總和。對式(5)等號兩邊取協方差計算,得到式(6)。式(5)、式(6)即為多工位裝配過程狀態空間模型矩陣表達和方差形式。
2 裝配順序矩陣
多工位裝配過程包含大量的工藝信息,在建模之前需要將這些工藝信息(如零件數、工位數、裝配順序、定位銷布局、被重定位的零件等)提煉出來;在設計裝配路線階段,需要對不同的裝配路線進行仿真,這就意味著大量工夾具的更換,即工藝信息的改變。裝配順序矩陣可以滿足頻繁改變工藝參數的需求,快速地提煉過程工藝信息。
裝配順序矩陣,即order矩陣形式如下:
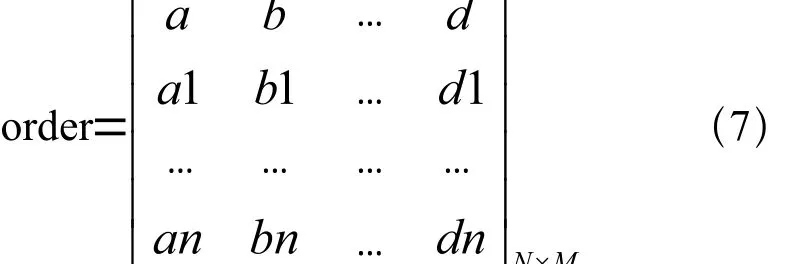
order矩陣有N行,代表裝配過程共有N個工位,每行元素代表該工位定位銷布局。每行前兩個元素代表總成件上定位銷布局,決定哪些零件被重定位。后面的元素代表待裝配零件的定位銷布局,決定零件裝配順序。沒有新零件裝配到總成件時用零元素代替,在編程建模時,使用continue語句結束當前工位的裝配操作。零件裝配順序矩陣可以確定零件總數和當前工位總成件的構成。
如圖2所示是典型的多工位裝配過程案例,其過程工藝參數可以由其裝配順序矩陣,即式(8)確定。式(8)中order矩陣有三行,確定裝配過程有3個工位。第一行元素有4個非零元素,說明在工位1兩個零件裝配形成總成件。第二行有6個非零元素,說明在工位2總成件與兩個新零件完成裝配。第三行只有前兩個元素非零,說明只有總成件被定位,工位3是測量工位。由每行奇數列的非零元素[13;157;1],可知零件裝配順序是零件1→零件2→零件3,4。由每行的前兩個元素[12;14;18],可知在工位2,零件1,2被重定位,在工位3零件1,4被重定位。


圖2 典型的多工位裝配過程案例
此外在設計裝配路線階段,改變order矩陣的元素就能達到改變裝配路線的目的。完成圖2產品的裝配,裝配順序矩陣還可以是:


圖3 優化裝配路線流程圖
式(9)代表另外三條裝配路線,即路線1:零件2→零件3→零件4→零件1;路線2:零件2→零件3→零件1→零件4;路線3:零件2→零件3,4→零件1。
裝配順序矩陣能夠實現對多工位裝配過程工藝信息的數學矩陣化處理,工藝信息的改變只要通過改變裝配順序矩陣的元素就能夠實現,調用order矩陣,利用循環語句可以快速構建狀態空間模型,對多條裝配路線仿真,預測偏差,完成裝配路線的最優設計。
利用狀態空間模型和裝配順序矩陣優化具體產品的裝配路線,具體過程如圖3所示,優化的裝配順序能夠減少輸入偏差(KCC偏差)對輸出偏差(KPC偏差)的影響,使得裝配系統更穩健,產品尺寸偏差越小,質量越高。
3 實驗分析
以某轎車車身側圍裝配過程為例構建偏差流狀態空間模型,預測零件尺寸偏差,實現工藝路線的最優選擇。側圍簡圖如圖4所示,裝配過程包括4個零件,即零件1—A柱、零件2—B柱、零件3—側頂、零件4—側板。這些零件為結構件,具有較大的剛度,定位采用3-2-1定位方式[8](一面兩銷定位和夾緊),零件通過焊接的方式連接到一起,滿足建模假設條件。按照圖3所示流程完成該產品的裝配路線優化設計。
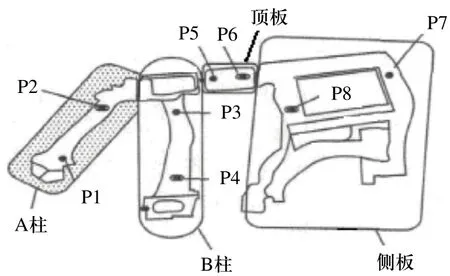
圖4 產品最終裝配效果圖

表1 定位銷P的坐標(單位:mm)

表2 測點S的坐標(單位:mm)
各零件上定位銷P(奇數點為四向定位銷,偶數點位兩向定位銷)和測點S坐標如表1,2所示。在設計裝配路線階段,擬定4套裝配路線,即:
路線1:零件1→零件2→零件3→零件4;
路線2:零件2→零件3→零件4→零件1;
路線3:零件2→零件3→零件1→零件4;
路線4:零件3→零件4→零件2→零件1。
上述四條工藝路線對應的裝配順序矩陣分別是:
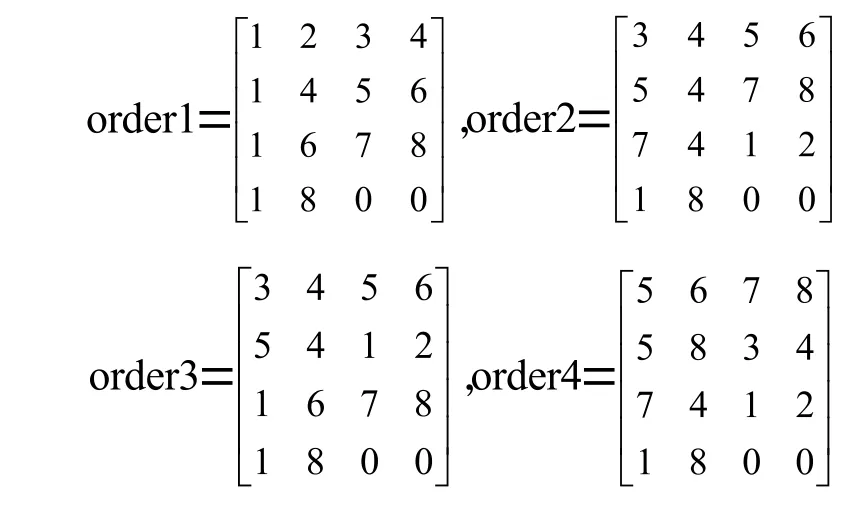
對于具體裝配路線各工位定位銷的選擇可以有很多種,本文采用最大距離原則選取定位銷定位,即選擇幾何距離最大的定位銷組定位。
根據已知條件和order矩陣,利用Matlab軟件編程構建偏差流狀態空間模型,由于篇幅限制,不再給出各裝配路線的系統矩陣A、輸入矩陣B、觀測矩陣C的具體形式,只給出第一條裝配路線Γ矩陣的具體形式,如下:

假設所有定位銷的定位偏差為±1mm,根據±3δ原則,定位偏差U∈N(0,1/6)。在Matlab中生成服從N(0,1/6)分布的隨機數組作為狀態空間模型的輸入向量,忽略噪聲項,應用式(5)進行100次仿真,最終預測各測點尺寸偏差如表3所示。
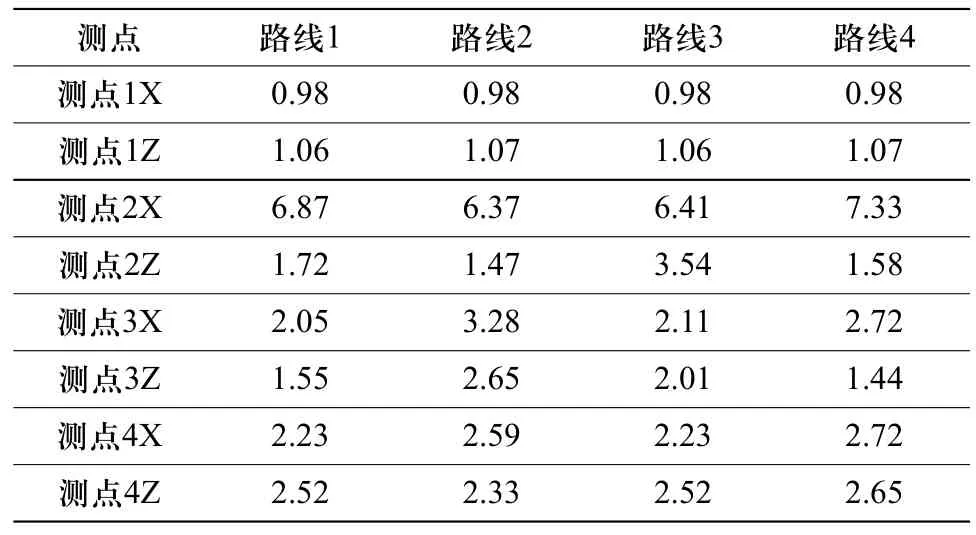
表3 測點尺寸偏差預測值(單位:mm)
由表3可知,四條裝配線路在測點1的預測中差異微小,不能單從測點1出發判斷裝配路線的優劣。路線1與路線2相比,在測點3和4處,尺寸偏差較小且與路線2差距明顯,路線1優于路線2;路線2與路線3相比,在測點3和4處,尺寸偏差略大,但在測點2處,尺寸偏差顯著的小于路線3,可知路線2優于路線3;路線4與路線2相比,在測點3處尺寸偏差顯著小于路線2,但在測點2上尺寸偏差顯著大于路線2,可知路線2和路線4優劣性相當,路線4略優于路線2。根據優劣性排序,路線1>路線4>=路線2>路線3。選擇路線1作為產品的裝配方案。
4 結論
提出基于偏差流狀態空間模型的多工位裝配順序矩陣,即order矩陣,實現對具體裝配工藝路線和過程工藝信息的數學矩陣化處理。在order矩陣的基礎上,利用循環語句在Matlab中建立參數化偏差流狀態空間模型,能夠對多工位裝配過程仿真,預測產品尺寸偏差,實現裝配路線最優設計。該模型為后續的偏差源診斷、夾具優化、測點優化等工作提供了數學基礎。
[1] Liu S, Hu S J.Variation simulation for deformable sheet metal assemblies using finite element methods[J].ASME Journal of Manufacturing Science and Engineering, 1997,119: 368-374.
[2] Hsieh C, Kong P.Simulation and optimization of assembly processes involving flexible parts[J].Journal of Vehicle Design, 1997, 18(5): 455-465.
[3] Lawless J F, Machay R J, Robinson J A.Analysis of ariation transmission in manufacturing processes–part I[J].Journal of Quality Technology, 1999, 31(2): 131-142.
[4] Jin J, Shi J.State space modeling of sheet metal assembly for dimensional control[J].ASME Journal of Manufacturing Science and Engineering, 1999, 121(4):756-762.
[5] 田兆青.轎車車身裝配偏差流的狀態空間建模方法及應用基礎研究[D].上海, 上海交通大學機械與動力工程學院, 2008.
[6] 文澤軍, 劉德順, 楊書儀.多工位裝配過程夾具系統公差和維護綜合優化設計[J].機械工程學報, 2009, 45(12):151-161.
[7] 田兆青, 來新民, 林忠欽.多工位薄板裝配偏差流傳遞的狀態空間模型[J].機械工程學報, 2007, 43(2): 202-209.
[8] CAI Wayne.Robust pin layout design for sheet-panel locating[J].International Journal of Advanced Manufacture Technology, 2006, 28(3): 486-494.

