水泥石膏材料相似模擬節理巖體有限元分析

王永亮，栗東平

(1.清華大學土木工程系，北京100084;2.河北工程大學 工程力學系，河北邯鄲056038)

實際工程中，現場巖體體積龐大，實際巖體強度的檢測難以實現，且測試費用較高，進而發展了在實驗室中利用小尺寸試件來模擬實際巖體的分析方法[1]，這就需要發展相應的相似理論[2－3]和相似模型。文[4]中利用水泥石膏材料來相似模擬巖體，通過實驗室大量的模擬試驗得到了模擬砂巖的配合比，顯示了該水泥石膏材料良好的性能。在該復合砂漿中，水泥作為粒狀漿材，可以提高復合砂漿的強度;石膏粉能調節復合砂漿的膠結時間。因此，該復合砂漿不但保留了水泥砂漿流動性好等優點，而且克服了水泥砂漿強度低的弱點，它大幅度提高了砂漿的抗壓強度和抗剪強度[5]，具有優良的復合性能，是一種較好的相似材料。

巖體是由巖塊和結構面組成的地質體，因此其強度必然受到巖塊和結構面強度及其組合方式的控制。一般情況下，巖體的強度不同于巖塊的強度，也不同于結構面的強度，如果巖體中結構面不發育，呈完整結構，則巖體強度大致等于巖塊強度，如果巖體將沿某一結構面滑動時，則巖體強度完全受該結構面強度的控制[6]。這兩種情況，相對比較好處理;本文將著重討論被節理切割的裂隙(節理化)巖體強度的確定問題。它一方面受巖石材料性質的影響，另一方面受結構面特征(數量、方向、間距、性質等)和附存條件(地應力、水、溫度等)的控制。本文將進一步利用上述水泥石膏材料相似模擬三維巖體，進行有限元分析，研究其不同節理傾角下的抗壓強度。

1 相似試驗研究

試驗原料水泥:42.5普通硅酸鹽水泥;石膏:特級熟石膏粉;硼砂:采用工業用硼砂(一等)，硼砂含量＞95%，在試驗中加入的硼砂濃度為1%;砂:模數為2.7的河砂(中砂)。

為了研究骨料對水泥石膏模擬材料性能的影響，做了固定水泥用量(200 g)和石膏用量(150 g)，逐漸增大砂用量的室內試驗，并在此基礎上繪制了隨砂含量的增大，水泥石膏模擬材料的抗壓強度、抗彎強度、彈性模量的變化曲線。隨著砂量的增大，水泥石膏模擬材料的抗壓強度和抗彎強度在小范圍內顯著減小。固定砂用量(1 900 g)和石膏用量(120 g)，研究水泥用量對水泥石膏模擬材料性能的影響。當固定砂和石膏用量時，水泥石膏相似材料的抗壓強度和抗彎強度在小范圍內隨水泥用量的增大呈明顯增大的趨勢。固定砂用量1 900 g、水泥用量200 g時 ，逐漸增加石膏的含量，研究石膏用量對水泥石膏模擬材料性能的影響。當固定砂和水泥用量時，水泥石膏相似材料的抗壓強度和抗彎強度在小范圍內隨石膏用量的增大呈明顯的增大趨勢。水膠比也是影響水泥石膏模擬材料的一個重要指標。當固定砂、水泥和石膏的用量時，水泥石膏模擬材料的抗壓強度和抗彎強度在小范圍內隨著用水量的增大呈明顯減小的規律。

在上述試驗分析結果的指導下，進行了相關試驗，得到模擬材料的抗壓強度范圍為2.10 MPa～6.30 MPa。

2 相似模型的有限元分析

2.1 有限元分析概述

分析強度問題，運用理想彈塑性模型[7－8]即可獲得比較精確的解答。摩爾－庫倫(M－C)屈服準則可很好地描述大多數巖土材料的強度特性[9－10]，因此本文采用M－C屈服準則。由于M－C屈服準則的屈服面為不規則的六角形截面的角錐體表面，存在尖頂和棱角，給有限元計算帶來很大的不便，為此需要修正。本文中所用軟件ANSYS采用的是廣義Mises準則[11]，其通式為

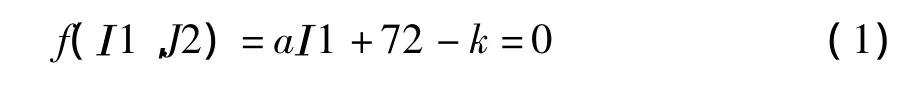
式中a、k為與c、φ有關的參數，變換a、k值就可在有限元中實現M－C系列修正的屈服準則。

從式(1)看，在平面應變條件下，M－C內切圓屈服準則采用關聯流動法則時與M－C屈服準則是一致的[12]，有很高的計算精度，因此本文選擇M－C內切圓屈服準則作為巖塊的屈服準則。

合理地分析和模擬節理的力學特性和破壞機制一直是工程界和學術界關注的熱點問題[13－15]。本文基于有限元軟件ANSYS，擬采用夾層模型來進行節理的數值模擬。假設結構面有一定的厚度(即巖塊中存在夾層)，采用與水泥石膏巖塊相同的常規實體單元，本構關系與屈服準則也與其一致，只是強度參數(粘聚力c、內摩擦角φ等)有所不同。

下面將通過對 0°、30°、45°、60°等各個角度的節理巖體進行模擬，進而得到各自的抗壓強度。對于各個角度模型的有限元分析具體步驟類似，下面主要討論45°情況，其它各模型類似討論可得相應結果。

2.2 45°傾角試塊的有限元分析

根據ANSYS采用SOLID65單元來模擬所選用的材料，建立30 mm×30 mm×60 mm的立方體幾何模型。節理的厚度為短邊邊長的1/20，即1.5 mm，這條單節理與水平面成45°夾角。將立體沿各個劃分后的長邊分成4份，短邊分成2份的有限元網格劃分方法，具體模型如圖1所示，參數設置見表1、表2。

表1 SOLID65單元參數Tab.1 SOLID65 parameters

表2 巖體塊與節理塊接觸對參數Tab.2 Rock blocks and joints contact parameters

根據試驗室的實際加載情況，考慮到試驗機的壓頭對試塊上下兩個面在各自平面內進行約束，因此，可將模型底部面上的各節點在X，Y、Z方向的位移進行約束，將頂部面上的節點在X、Z方向的位移進行約束。為了保證壓力均勻，在試件頂部面上的Y方向施加10.0 MPa的壓力載荷，在求解過程中，打開自動時間步，即可自動選擇合適的荷載步增量，逐步加載到試件的頂部。在分析計算過程中，不考慮溫度的影響，采用力收斂和位移收斂相結合的收斂準則，打開線性搜索選項，輸出每一步的計算結果，打開程序的自動二分選項，設置終止時間為1，設置50個子步，每一個子步的不平衡迭代次數為35步，每個載荷子步結果都輸出到結果文件中。

結果后處理分析:通過對30 mm×30 mm×60 mm尺寸的試件進行模擬計算，可以得出隨著載荷步和時間的增加，載荷與位移(Y軸方向)的數據。當時間進行到 Time=0.648 47時，結構破壞，程序由于不收斂而結束計算，得出相應荷載－位移曲線，如圖2所示。

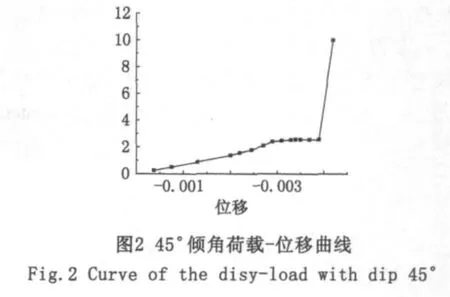
由圖2可以看出，荷載－位移變化關系基本上分為三部分:第一部分0－2.414 47階段，這一階段曲線基本成直線，而且曲線的斜率基本比較陡;第二部分2.414 47－2.561 57階段，這一階段曲線的變化基本比較平緩;第三階段2.56157－10.000 00階段，這一階段，曲線就是一條直線。從圖2上可以看出:首先是節理面的上力所產生的變形，在這一階段模型的變形基本以彈性變形為主，第一段斜直線部分，然后是節理面尖端產生的變形，最后為產生裂紋，并且這一階段最明顯的特征為，位移持續增大，而荷載變化很小，如圖2中間平緩部分，在這一階段末和下一階段初，模型失去承載力，因此可以認為，第二階段末和第三階段初所對應的荷載即為這一尺寸試件的極限荷載，即Pmax=2.561 57 MPa。這也正好和試驗室中試塊的破壞形式基本上一致。模型受力過程中，從不同子步應力變化可以看出:隨著荷載的加大，模型的節理附近的應力變大，這與試驗中對應試塊的裂紋在中部節理部位產生的現象相吻合，如圖3所示。當 substep=14，t=0.648 47時，變形急劇增大，也表明節理巖體達到了其極限載荷。

2.3 0°、30°、60°傾角試塊的模擬分析

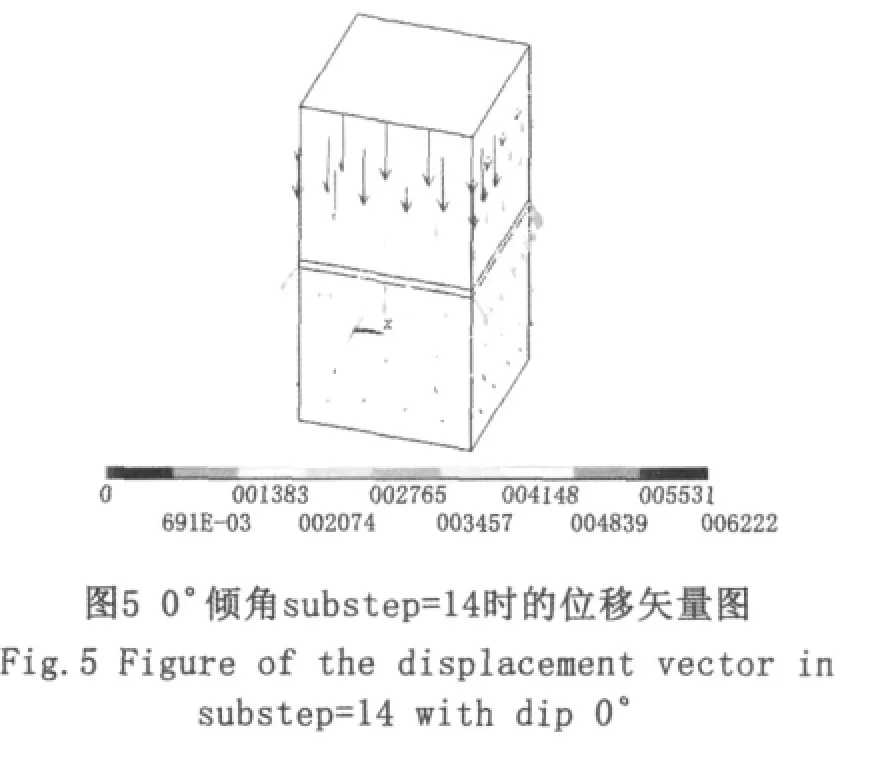
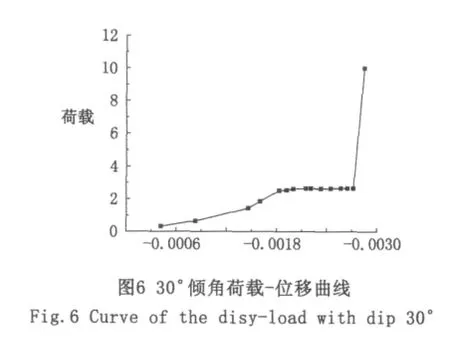
當傾角為0°時，時間進行到 Time=0.777 35時，程序由于不收斂而結束計算，得出荷載－位移曲線，如圖4所示。第二階段末和第三階段初所對應的荷載即為這一尺寸試件對應的極限荷載，即Pmax=4.720 69 MPa。如圖5所示，當 substep=14時，對應模型中部的應力出現大面積變大，由此可以斷定當t=0.777 35時對應的荷載即為其極限荷載;并且，由位移矢量也可以看出t=0.777 35時，變形急劇增大，也表明節理巖體達到極限載荷。同理，30°、60°傾角情況，極限荷載分別為Pmax=2.655 61 MPa、Pmax=6.488 86 MPa，分別如圖6、圖7、圖 8、圖 9 所示。

3 抗壓強度與有限元果分析

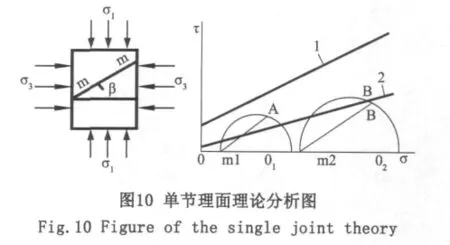
為了從理論上用分析法研究裂隙節理的抗壓強度，耶格(Jaeger)提出了單結構面理論。單節理面理論分析如圖10所示。

巖體中發育一組結構面AB(m－m)，假定AB面(指其法線方向)與最大主應力方向夾角為β，由莫爾應力圓理論，作用于AB面上的法向應力σ和剪應力τ為

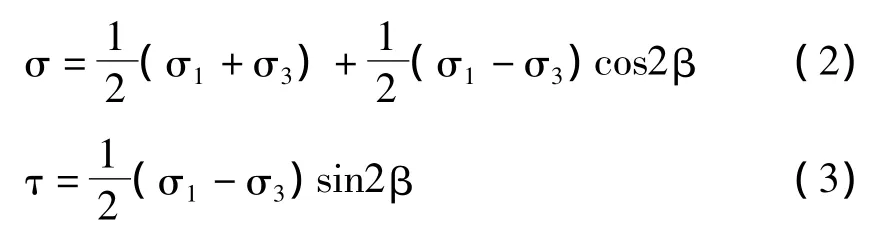
結構面強度曲線服從庫倫準則

式中cω，φω分別為結構面的粘結力和內摩擦角。

文[16]中采用PLANE42單元，與本文同樣利用夾層模型來模擬單節理巖體，建立平面模型，得到節理在不同傾角下巖石地基的承載力值。結合上文得到的單節理巖體抗壓強度模擬值和理論值，可以得出三者在節理傾角變化時的數據匯總，如表3所示。

表3 各抗壓強度隨傾角的變化Tab.3 Every intensity of pressure with the change of the angle

根據表3中數據可以得到傾角－抗壓強度曲線，如圖11所示。由圖11可以看出:

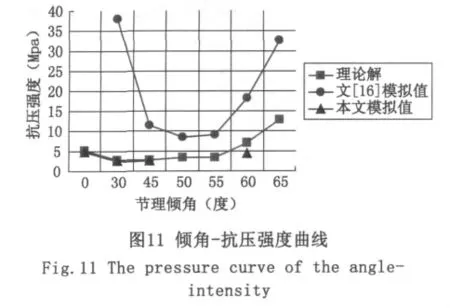
1)本文水泥石膏相似模型的抗壓強度與理論值十分接近，可以認為建立該相似模型是符合實際情況的。

2)將本文有限元分析結果與理論值、文[16]結果進行比較、分析，可以看出三者的變化趨勢是相同的，即單個節理巖體的抗壓強度并不是隨著該節理傾角的變化而單調遞增或遞減，而是隨著傾角的逐漸增加，抗壓強度先是逐漸減少到一個最小值，而后逐漸增加。

3)文[16]中所得到的強度值均比理論值和本文的模擬值明顯偏大，是因為其所用的參數完全是巖體的實際參數，建立的平面模型，模擬的是真實的巖體。而本文中用到的參數是根據實驗室中模擬巖體的水泥石膏試塊所具有的參數來確定的，建立的是三維實體模型，理論值也是根據該參數來進行求解的，所以理論值與本文模擬值相近。若調整水泥石膏材料中的用料配比，也可以對文[16]中的真實巖體進行模擬。

4 結論

1)其承壓破壞方式與實際節理巖體破壞方式相似，進而驗證了水泥石膏相似模擬巖體的可行性。

2)本文僅考慮單節理的巖體強度，實際巖土工程中更多的是多節理的巖體，相應分析也會更加復雜。巖體的強度不單單與節理傾角有關，還與巖石強度、節理位置、周圍環境等等有關。對于水泥石膏模擬巖體，也應當進一步考慮模型的尺寸效應。

[1]林韻梅.實驗巖石力學－模擬研究[M].北京:煤炭工業出版社，1984.

[2]左保成，陳從新，劉才華.相似材料試驗研究[J].巖土力學，2004，25(11):1805－ 1808.

[3]彭海明，彭振斌，韓金田.巖性相似材料研究[J].廣東土木與建筑，2002，12(12):13－17.

[4]栗東平，王謙源，張增祥，等.模擬巖性的相似試驗研究[J].河北工程大學學報:自然科學版，2007，24(2):12－19.

[5]黃戡，卿凇，謝國柱.水泥石膏相似材料的模擬實驗[J].西部探礦工程，2003，15(12):127－129.

[6]GHOSH A，DAEMEN J J K.Fractal characteristics of rockdiscontinuities[J].Engineering Geology，1993(34):1－9.

[7]趙德安.節理塑性對巖體性能的影響分析[J].蘭州鐵道學院學報，2002，21(4):1 －4.

[8]ZHAO DEAN.Impact of joint plasticity to properties of rock mass[J].Journal of Lanzhou Railway University(Natural Sciences)，2002，21(4):123－127.

[9]蔡美峰，何滿潮，劉東燕.巖石力學與工程[M].北京:科學出版社，2002.

[10]李曉紅，王成.含節理的巖石地基承載力估算[J].工程力學(增刊)，2001:659－662.

[11]WU JIMIN，A.MABTAB，XU SHULIN.Estimation the barton equation for the shear strength of rock joints[J].Journal ofEngineeringGeology;2007(04):0349－0353.

[12] CARPINTERI A.Scaling law and renormalization groups for strength and toughness of disordered materials[J].International Journal of Solids and Structures，1994(31):610－613.

[13]張志剛，喬春生，劉勇.節理巖體強度特征研究綜述[J].煤田地質與勘探，2006，34(5):38－41.

[14]張志剛，喬春生，李 曉.單節理巖體強度試驗研究[J].中國鐵道科學，2007，28(4):34 －39.

[15]張志剛，喬春生.改進的節理巖體強度參數經驗確定方法及工程應用[J].北京交通大學學報，2006，30(4):46－49.

[16]鄧楚鍵，孔位學，鄭穎人.節理巖石地基極限承載力的有限元分析[J].工業建筑，2005，35(12):51－54.