具有旋轉對稱根的多項式的牛頓映照

劉剛

(衡陽師范學院數學與計算科學系,湖南衡陽 421002)

具有旋轉對稱根的多項式的牛頓映照

劉剛

(衡陽師范學院數學與計算科學系,湖南衡陽 421002)

主要研究特殊多項式的牛頓映照的動力學性質.通過研究根的分布和重數,揭示了當多項式的根關于某點具有一定的旋轉對稱性,且對稱根的重數都相同時,此類多項式的牛頓映照要么是雙曲的,要么是次雙曲的.另外多項式的牛頓映照的動力學性質為多項式的某些問題提供了新的思路.

牛頓映照;Julia集;雙曲;次雙曲

1 引言及主要結果

給定多項式f,則如下定義的公式

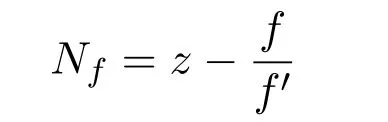
稱之為關于多項式f的牛頓映照,簡稱為牛頓映照.牛頓映照Nf的有限不動點與f的根一一對應,進一步而言,f的根為Nf的(超)吸性不動點.因此牛頓映照迭代給出了多項式的一種求根算法,該算法即為經典的牛頓方法.很多數學工作者從復動力系統的角度對其進行了研究,文獻[1]證明了所有根的直接吸引域是單連通的.隨后文獻[2]利用擬共形手術得到牛頓映照的Julia集是連通的.文獻[3]對三次多項式的牛頓映照進行了組合分類.文獻[4]利用Yoccoz拼圖片的方法證明了存在一個三次多項式,它的牛頓映照具有Cremer點但其Julia集仍可局部連通,此性質與多項式的動力學性質截然相反.關于牛頓映照Julia集的對稱性問題,可參見文獻[5].盡管已有很多關于牛頓映照的動力學結果,然而對高次多項式的牛頓映照,其結果相對較少且缺乏好的分析方法.

研究牛頓映照的一個重要的簡化途徑為標量定理(見引理2.1),該定理告訴我們牛頓映照的動力學性質某種程度上決定于根的分布及其重數,而與位置沒有關系.本文旨在通過研究多項式根的特殊分布及其重數,從而其牛頓映照具有好的動力學性質.下記(f,g)為多項式f和g首一的最大公因式,?f為f不同根的數目.本文獲得的主要結果為:

定理1.1 從復平面上一點ξ向無窮遠處引n(≥2)條射線,且任意相鄰的兩條射線所夾的角度相等.若多項式f的根都分布在這n條射線上,另外還滿足如下條件之一:

(1)n=2;

(2)n為奇數,ξ為f的根(任意重數),其它的根以ξ為對稱中心均勻地分布在上述n條射線上,且任何兩個到ξ距離相等的根的重數相同;

(3)n為大于2的偶數,此時將這n條射線分為兩組,每組相鄰的兩條射線所圍成的扇形區域恰好包含另一組的一條射線.ξ為f的根(任意重數),且每組射線上的根以ξ為對稱中心進行均勻地分布,且每組上任何兩個到ξ距離相等的根的重數相同;

則Nf是雙曲的.

若在上述定理條件(2)和(3)中,對稱中心不是該多項式的根,該類多項式的牛頓映照的動力學仍難以刻畫,然而在特殊情況下有如下結論.

定理1.2 從復平面上一點ξ向無窮遠處引n(≥3)條射線,且任意相鄰的兩條射線所夾的角度相等.若多項式f所有的根以ξ為對稱中心均勻地分布在這n條射線上,且所有根的重數(記為m)都相同,但ξ不為f的根,則Nf是次雙曲的.

以上兩個定理,實際上要求f的根關于某點具有一定的旋轉對稱性,且相應旋轉對稱根的重數相同.

滿足定理1.1條件的多項式為定理1.3提供了豐富的具體例子,此時無需計算便有相關的結論.對于非雙曲的例子,有無重根難以決定,但定理1.3中的不等式在一定情形可以改進(例如考慮定理1.2中情形).進一步的研究,更多關于多項式的某些問題可從復動力系統的角度進行考慮.

2 相關定義及引理

其中c為非零的常數.

該引理的意義在于,對于給定的多項式,將其所有的根整體做平移,旋轉,伸縮后所構成的新多項式的牛頓映照的動力學與原多項式的牛頓映照的動力學一致.為證明文中結果,還需以下的定義和引理.

引理 2.2[2]對任意非常數的多項式f,其對應的牛頓映照的Julia集J(Nf)是連通的.

定義 2.2 (到無窮的趨近)在B?(ξ)中以 ξ為起點且通向無窮的定端同倫曲線族稱之為B?(ξ)的一個到無窮的趨近.

3 主要定理的證明

命題 3.1 (1)設多項式 f的根關于直線 l對稱且對稱根的重數相同,則 J(Nf)和任意Fatou分支也關于該直線對稱.特別地,實系數多項式的牛頓映照的J(Nf)和任意Fatou分支關于實軸對稱.

(2)若實系數多項式f至少有三個不同的實根,則對于任意介于最小與最大實根之間的實根x,則B?(x)含有正偶數個Nf的臨界點.

滿足該定理條件的多項式在牛頓法下的分形圖集見圖1.

圖1 J(Nf)(多項式f(z)滿足定理1.1中條件)

圖2 J(Nf)(多項式f(z)滿足定理1.2中條件)

2.即使多項式的根關于實軸,虛軸,原點對稱,且所有根的重數都相同,其相應的牛頓映照的動力學性質也難以分析.例如實四次多項式族fc(z)=(z2+1)(z2?c)(c∈{0})的牛頓映照,階大于1的吸性域,拋物域,Siegel盤均可能出現.

圖3 J(N~f),J(Nf0.12)和J(Nf0.16)

[1]Przytycki F.Remarks on the Simple Connectedness of Basins of Sinks for Iterations of Rational Maps[M]// Krzyzewski K.Dynamical Systems and Ergodic Theory.Warsaw:Babach Center Publications,1989.

[2]Shishikura M.The Connectivity of the Julia Set of Rational Maps and Fixed Points[M]//Schleicher D. Complex dynamics:Families and Friends.Wellesley:A K Peters,2009.

[3]Tan Lei.Branched coverings and cubic Newton maps[J].Fund.Math.,1997,154(3):207-260.

[4]Roesch P.On local connectivity for the Julia set of rational maps:Newton′s famous example[J].Ann.Math., 2008,168:1-48.

[5]陽衛鋒.牛頓變換Julia集的對稱性[J].純粹數學與應用數學,2009,25(3):530-533.

[6]Beardon A F.Iteration of Rational Functions[M].Berlin:Springer,1991.

[7]Carleson L,Gamelin T W.Complex Dynamics[M].Berlin:Springer,1991.

[8]Milnor J.Dynamics in One Complex Variable[M].3rd ed.Princeton and Oxford:Princeton University Press,2006.

[9]喬建永.重整化變換的復動力學[M].北京:科學出版社,2010.

[10]Hubbard J,Schleicher D,Sutherland S.How to fi nd all roots of complex polynomials by Newton′s method[J]. Invent.Math.,2001,146(1):1-33.

Newton maps for polynomials with rotationally symmetric roots

Liu Gang
(Department of Mathematics and Computational Science,Hengyang Normal University, Hengyan 421002,China)

The dynamical properties of Newton maps for special polynomials are investigated.Analysis of the distribution and multiplicities of roots revealed that Newton maps for polynomials,whose roots are some rotationally symmetric with a fi xed point and the multiplicities of symmetric roots are all the same,are either hyperbolic or subhyperbolic.Moreover,the study of dynamical properties of Newton maps for polynomials produce new ideas for some problems of polynomials.

Newton map,Julia set,hyperbolic,subhyperbolic

O174.5

A

1008-5513(2012)05-0628-07

2011-10-20.

中央高校基本科研業務費(2010YS02).

劉剛(1982-),博士生,研究方向：復動力系統.

2010 MSC:37F45