帶強迫項變系數組合KdV方程的有理展開式精確解

劉娟

(河南理工大學數學與信息科學學院,河南 焦作 454000)

帶強迫項變系數組合KdV方程的有理展開式精確解

劉娟

(河南理工大學數學與信息科學學院,河南 焦作 454000)

利用符號計算軟件Maple,在一個新的廣義的Riccati方程有理展開法的幫助下,求出了帶強迫項變系數組合KdV方程的有理展開式的精確解,該方法還可被應用到其他變系數非線性發展方程中去.

廣義的Riccati方程有理展開法;變系數組合KdV方程;強迫項;類孤波解

1 引言

物理學中的很多現象都可以用非線性發展方程來描述.在研究非線性物理現象中,尋找非線性發展方程(NEEs)的精確解起著非常重要的作用并引起了越來越多學者的興趣,多年來許多數學家、物理學家為此做了大量的工作[118].常系數非線性方程只能近似地反映實際物質運動變化規律,而變系數非線性方程卻能更加準確地描述物質的屬性,因此研究變系數非線性方程的精確解顯得十分重要.近年來,人們已經發現了一些有效的求解方法,如變分法、截斷展開法、齊次平衡法、B¨acklund變換法、F-展開法、分離變量法、Jacobi橢圓函數法、形變映射法等[1115].沿著有理展開的思路,本文提出了一種新的代數方法,稱為新的廣義的Riccati方程有理展開法,來求解帶強迫項變系數組合KdV方程:

其中 α(t),m(t),β(t),R(t)為 t的任意函數.當 R(t)=0,α(t),m(t),β(t)為常數時轉化為組合KdV方程,該方程是KdV和mKdV方程的復合,廣泛應用于等離子體物理、固體物理、原子物理、流體力學和量子常理論等領域.在等離子體物理中它描述了無Laudau衰變小振幅離子聲波的傳播,在固體物理中用于解釋通過氟化鈉單晶的熱脈沖傳播,同時還可以很好地描述在具有非諧束縛粒子的一維非線性晶格中波的傳播,又可作為流體力學中的一個模型方程;當R(t)=0,α(t)=0,m(t),β(t)為常數時轉化為mKdV方程,用來描述非調和晶格中聲波的傳播和一個無碰撞等粒子體的Alfen波的運動;當R(t)=0,m(t)=0,α(t),β(t)為常數時轉化為KdV方程,眾所周知,它是最典型的非線性色散波動方程的代表.因此,研究方程(1)的精確解有重要的理論和實際價值.

2 方法概述

下面,敘述這個方法的主要內容.

對于物理學中給定的關于x,t的包含兩個變量的非線性發展系統:

3 帶強迫項變系數組合KdV方程的有理展開式精確解

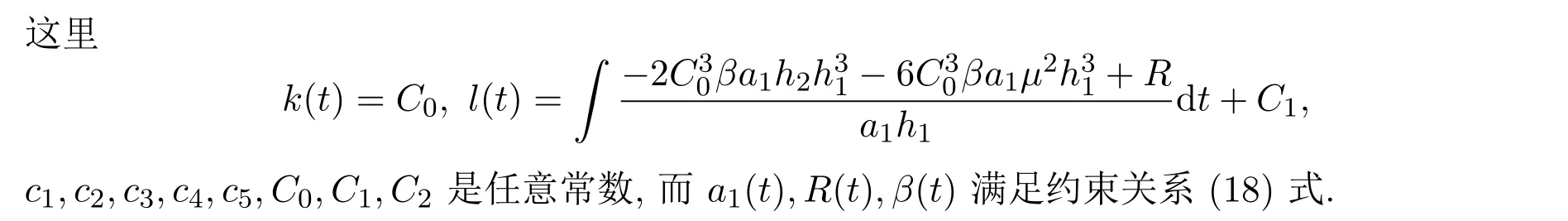
注 3廣義性:i)如果將(4)式中的參數h1和h2取不同的值,則tanh函數展開法[7],廣義的Tanh函數展開法[8],改進的擴展的tanh函數展開法[9],廣義的雙曲函數法[10],Riccati方程有理展開法[11]和廣義的Riccati方程有理展開法[12]都可以由新方法得到,即這里提出的方法更具有一般性.ii)文獻[3-10]中常系數KdV方程的解是常數,為變量的線性函數,在變系數KdV方程中去掉了這些限制,使之成為更一般的函數,從一定意義上來說更具有一般性.

注 4可行性:由于本文中降低了對未知量的限制,自然就增加了計算的復雜程度,盡管計算機符號系統可以進行復雜繁瑣的計算,但有時還是困難的,甚至是不可能的.為此,對于未知函數不得不嘗試一些特殊函數以使得到的微分方程可解.

4 結論

本文構造了一種新的廣義的Riccati方程有理展開法,將Riccati方程做了推廣,使之結果更一般,適普性更強,并得到了更一般的新解.并且,運用此方法成功求出了帶強迫項變系數組合KdV方程的一些精確解,包括類周期解,類孤波解等,由于實踐證明這種方法可以適用于許多其他非線性方程.另外,如何將該方法推廣到變系數的具有任意次冪項的非線性KdV方程,還值得進一步的研究.

[1]Ablowitz M J,Clarkson P A,Soliton,Nonlinear Evolution Equations and Inverse Scatting[M].Cambridge: Cambridge University Press,1991.

[2]Chen Y,Wang Q.Auto-B¨acklund transformation and exact solutions for modi fi ed nonlinear dispersive mK (m,n)equations[J].Chaos,Solitions and Fractals,2003,17:693-698.

[3]Lou S Y,Lu J Z.Special solutions from variable separation approach:Davey-Stewartson equation[J].J. Phys.A,1996,29:4209-4215.

[4]Matveev V A,Salle M A.Darboux Transformations and Solitons[M].Berlin,Heidelberg:Springer-Verlag, 1991.

[5]Hu X B,Ma W X.Application of Hirota′s bilinear formalism to the Toeplitz larrice-some special solitonlike solution[J].Phys.Lett.A,2002,293:161-165.

[6]Parjes E J,Du ff y B R.Travelling solitary wave solutions to a compound KdV-Burgers equation[J].Phys. lett.A,1997,229:217-220.

[7]Khater A H,Mal fl iet W,Callebaut D K,et al.The tanh method,a simple transformation and exact analytical solutions for nonlinear reaction-di ff udion equations[J].Chaos,Solitons and Fractals,2002,14:513-522.

[8]Fan E G.Extended tanh-function method and its applications to nonlinear eqiatopms[J].Phys.Lett.A, 2000,277:212-218.

[9]Elwakil S A,Ek-labany S K,Zahran M A.Modi fi de extended tanh-function method for solving nonlinear partial di ff erential equations[J].Phys.Lett.A,2002,299:179-188.

[10]Gao Y T.Tian B.Generalized hyperbolic-function method with computerized symbolic computation to construct the solitonic solutions to nonlinear equations of mathematical physics[J].Comput.Phys.Comm., 2001,133:158-164.

[11]Wang Q,Chen Y,Zhang H Q.A new Riccati equation rational expansion method and its application to(2+1)-dimensional Burgers equation[J].Chaos,Solitons and Fractals,2005;25:1019-1028.

[12]Wang J,Zhang X L,Song L N,et al.A new general algebraic method with symbolic computation and its application to two nonlinear di ff erential equations with nonlinear terms of any order[J].Appl.Math. Comput.,2006,182:1330-1340.

[13]Lu D C,Liu G L.A sub-ODE method for generalized Gardner and BBM equation with nonlinear terms of any order[J].Appl.Math.Comput.,2010,217:1404-1411.

[14]Yan Z Y.New explicit travelling wave solutions for two new integrable coupled nonlinear evolution equations[J].Phys.Lett.A,2001,292:100-106.

[15]王明亮.齊次平衡法原則及其應用[J].蘭州大學學報:自然科學版,1999,35(3):8-15.

[16]Clarkson Peter A,Kruskal Martin D.New similarity reductions of the Boussinesq equation[J].Math.Phys., 1989,30:2201-2213.

[17]Tang X Y,Lin J.Conditional similarity reductions of Jimbo-Miwa equation via the classical Lie group approach[J].Commun.Theor.Phvs.,2003,39:6-8.

[18]盧殿臣,洪寶劍.帶強迫項變系數組合KdV方程的顯示精確解[J].物理學報,2006,55(11):5617-5622.

Exact solution of rational expansion method to the variable coefficient combined KdV equation with forced term

Liu Juan
(Department of Mathematics and Information,Henan Polytechnic University,Jiaozuo 454000,China)

With the aid of symbolic computation system Maple,several new kinds of generalized exact solutions for the variable coefficient combined KdV equation with forced term are obtained by using a new generalize Riccati equation rational expansion method.This approach can also be applied to other variable coefficient nonlinear evolution equations.

generalized Riccati equation rational expansion method, variable coefficient combined KdV equation,forced term,solitary-wave-like solutions

O175.2

A

1008-5513(2012)05-0705-06

2012-05-10.

國家自然科學基金(61104119).

劉娟(1977-),碩士,副教授,研究方向：機械化數學和孤立子理論.

2010 MSC:35Q53