Banach空間中一類序壓縮映射的不動點定理

卜香娟

(西北大學數學系,陜西西安 710127)

Banach空間中一類序壓縮映射的不動點定理

卜香娟

(西北大學數學系,陜西西安 710127)

在Banach空間中,利用迭代方法,研究了滿足一定條件的序壓縮算子的一些性質,獲得了一類序壓縮映射的不動點定理,證明了相應的結果,推廣和改進了原有的結論,使其應用范圍更加廣泛.

序Banach空間;正規錐;不動點;序壓縮算子

1 引言及基本概念

近年來,很多學者研究了實Banach空間以及序Banach空間[1]中序壓縮映射的不動點定理,文獻[2]引入了幾種按序壓縮的壓縮性映射,并證明了相應的不動點定理,本文在較弱的條件下討論了一類序壓縮映射的不動點定理并給出了證明,推廣了已知的結果.

定義1.1[3]設E是Banach空間,P為E的子集,若P滿足:

(i)P是非空凸子集

(ii)?x∈P以及?λ＞0,λx∈P;

(iii)若x∈P且-x∈P,則x=θ.

則P是一個以θ為頂點的錐.給定E中的錐P,可以定義E中的偏序關系:

若x,y∈E,y-x∈E,則稱x≤y.若P是E中的錐,若存在常數N＞0,使得對θ≤x≤y,有‖x‖≤N‖y‖,則稱P是正規的,N為正規常數.

定義1.2[3]設“≤”是由錐P確定的半序,對u,v∈E,若有u≤v或v≤u之一成立,則稱u和v是可比較的.當u和v是可比較時,若v≤u,則記u∨v=u;若u≤v,則記u∨v=v.

引理1.1[2]若u和v是可比較的,則u-v和v-u也是可比較的,且

引理1.2[2]若u和v,u和w,v和w是可比較的,則引理1.3[2]若對所有的n,u和vn是可比較的,且vn→v0,則u和v0是可比較的.

引理1.4[2]若對所有的n,un和vn是可比較的,且

則u0和v0是可比較的.

2 主要結果

定理2.1[47]設E是實Banach空間,P為正規錐,正規常數為N,設映射A:E→E滿足:

(i)?u,v∈E,若u和v是可比較的,則Au與Av也是可比較的;

(ii)存在單調遞增的映射α(t):[0,∞)→(0,1),使得

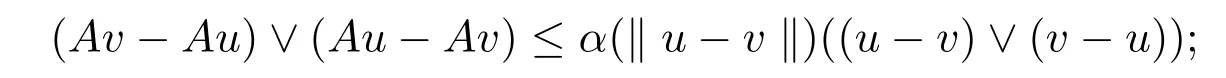
(iii)存在x0∈E,使得?n,x0和Anx0是可比較的,則A存在不動點,且迭代序列{Anx0}收斂于A的一個不動點x*,進而

由條件(ii),當n=1時,x0與Ax0是可比較的,又由條件(i),

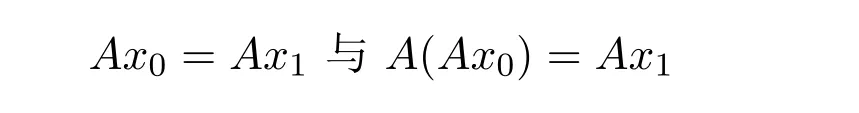
是可以比較的,即x1與Ax1是可以比較的,由歸納法得:?n,xn與Axn是可比較的,且由P的正規性及引理1.4,存在與范數‖·‖等價的范數‖·‖1,關于P是單調的,即存在0＜μ＜λ,使得:μ‖·‖1≤‖·‖≤λ‖·‖1,所以由α的單調遞增性得:α(‖·‖)≤α(λ‖·‖1).

由條件(i)得:

令t=λ‖x1-x0‖1,則結論成立.

定理2.2設E是實Banach空間,P為正規錐,正規常數為N,設映射A:E→E連續,且滿足:

(i)?u,v∈E,若u和v是可比較的,則Au與Av也是可比較的,又有u和Au是可比較的,v和Av是可比較的;

(Av-Au)∨(Au-Av)≤α(‖u-v‖)((Au-u)∨(u-Au)+(Av-v)∨(v-Av));

(iii)存在x0∈E,使得對x0與Ax0是可比較的,則A存在不動點,且迭代序列{Anx0}收斂于A的一個不動點x*,進而

由條件x0與Ax0是可比較的及條件(i)歸納得出:?n,xn與Axn是可比較的,由P的正規性及引理1.4,存在與范數‖·‖等價的范數‖·‖1,關于P是單調的,即存在0＜μ＜λ,使得:

令t=λ‖x1-x0‖1,則結論成立.

定理2.3設E是實Banach空間,P為正規錐,正規常數為N,設映射A:E→E連續,且滿足:

(i)?u,v∈E,若u和v是可比較的,則Au與Av也是可比較的,又有u和Au是可比較的,v和Av是可比較的;

(Av-Au)∨(Au-Av)≤α(‖u-v‖)((Au-u)∨(u-Au)+(Av-v)∨(v-Av));

(iii)存在x0∈E,使得對所有n,x0與Anx0是可比較的,則A存在不動點,且迭代序列{Anx0}收斂于A的一個不動點x*,進而

證明如同定理2.2的證明,可證迭代序列xn=Anx0是柯西序列,由于E完備,可設xn→x*∈E,下面證明x*是A的一個不動點.如同定理2.1的證明,可得對所有的n,xn與x*是可比較的,由條件(i),對所有n,xn=Axn-1與Ax*是可比較的.令n→∞,得x*與Ax*是可比較的,從而

上式表明:Ax*=x*,即x*為A的一個不動點.定理的后半部分類似于定理2.2可證明.

定理2.4設E是實Banach空間,P為正規錐,正規常數為N,設映射A:E→E為連續映射,且滿足:

(i)?u,v∈E,若u和v是可比較的,則Au與Av也是可比較的,又有u和Av是可比較的,v和Au是可比較的;

(Av-Au)∨(Au-Av)≤α(‖u-v‖)((Au-v)∨(v-Au)+(Av-u)∨(u-Av));

(iii)存在x0∈E,使得x0與Ax0是可比較的,且x0與A2x0是可比較的.則A存在不動點,且迭代序列{Anx0}收斂于A的一個不動點x*,進而

[1]郭大鈞.非線性泛函分析[M].濟南:山東科技出版社,2000.

[2]張憲.序壓縮映射的不動點定理[J].數學學報,2005,48(5):973-978.

[3]孫秀來,俞國華.一類變序算子的不動點定理的討論[J].寧波大學學報,2011,24(4):83-86.

[4]張石生.不動點理論及應用[M].重慶:重慶出版社,1984.

[5]李春平,郭春梅.一類變序算子的不動點定理[J].應用泛函分析學報,2007,9(5):259-265.

[6]衛亞茹,王海霞,黃梅娟.一類單調算子的不動點定理[J].純粹數學與應用數學,2008,24(4):806-809.

[7]彭榮.Banach空間中一類序壓縮算子的不動點定理[J].西南民族大學學報,2011,37(1):39-43.

Fixed point theorem s for a class of ordered contraction mapping in ordered Banach spaces

Bu Xiangjuan
(Departm ent of Mathem atics,Northwest University,X i′an 710127,China)

In Banach spaces,by using the iterativem ethod,this paper studies the order contraction m apping, which satisfies some properties.Fixed point theorem s for a class of ordered contraction mapping in Banach spaces are obtained and proved,which extends and im p roves the original results.

ordered Banach spaces,norm al cone,fixed point,order contraction m apping

O177.9

A

1008-5513(2012)03-0333-09

2012-01-09.

陜西省自然科學基金(2012JM1017).

卜香娟(1987-),碩士生,研究方向：非線性泛函分析.

2010 MSC:47H10