初始的L-外部空間
馬英,李令強,孟廣武
(聊城大學數學院,山東聊城 252059)
初始的L-外部空間
馬英,李令強,孟廣武
(聊城大學數學院,山東聊城 252059)
研究了初始的L-外部空間.構造了L-外部空間范疇的初始結構,并由此定義了L-外部空間的乘積結構和子空間結構,證明了L-外部空間范疇是L-預外部空間范疇的余反射子范疇.
L-外部空間;L-拓撲空間;初始的L-外部空間
1 引言及預備
自從文獻[1]把模糊集理論引入拓撲以來,很多學者從不同的角度出發討論了各種各樣的模糊拓撲理論[15].按照H¨ohle[5]的概念和符號,根據模糊化程度的不同模糊拓撲可以分為三種類型:(1)L-拓撲(集合是模糊的拓撲是分明的);(2)Fuzzifying拓撲(集合是分明的拓撲是模糊的);(3)L-模糊拓撲(集合和拓撲都是模糊的),其中L為某個格結構.同時,人們還研究了比模糊拓撲更為廣泛的空間結構,比如L-閉包空間、L-內部空間[38]、L-保序算子空間[9]等.文獻[10]引入了L-外部空間的概念,并且證明了逆冪等的L-外部空間與L-拓撲空間是一一對應的.本文將繼續對這一概念展開討論,構造了L-外部空間范疇的初始結構,并由此定義了L-外部空間的乘積結構和子空間結構,證明了L-外部空間范疇是文獻[11]的L-預外部空間范疇的余反射子范疇.
如未加說明,本文中的L表示帶有逆序對合對應完備的Heyting代數.有關L-拓撲的概念和結論請參考文獻[4-6],有關范疇的概念請參考文獻[12].
定義1.1[5]設f:X→Y是普通映射,則f誘導出一個從LX到LY的序同態,稱為L-值Zadeh型函數,記作f→:LX→LY,這里
定義1.2設(X,e1)與(Y,e2)為兩個L-外部空間,f:X→Y是普通映射.稱f為連續的.若?B∈LY,有
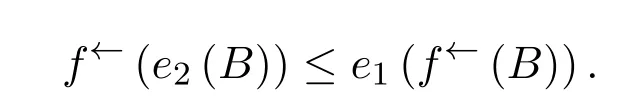

2 主要結果
定義2.1[10]設X為非空集,稱映射e:LX→LX為X上的一個L-外部算子若:
(1)e(0)=1;(2)e(A)≤A′;(3)e(A∨B)=e(A)∧e(B),稱序對(X,e)為L-外部空間,如果:(4)e((e(A))′)=e(A),稱e為逆冪等的.
定義2.2[11]稱映射e:LX→LX為X上的一個L-預外部算子,如果它滿足定義2.1中(1),(2),(4)和條件(3):e是逆序的,即當A,B∈LX且A≤B時,e(A)≥e(B).
定理2.1[10]設(X,δ)是一個L-拓撲空間,則映射eδ:LX→LX,
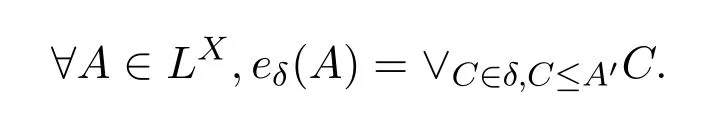
為X上的一個L-外部算子.
定義2.3設e1與e2均為X上的L-外部算子,稱e1比e2細(或e2比e1粗)若e1≥e2.
定理2.2設{(Xi,ei)}i∈Γ為一族L-外部空間,X為一集合,fi:X→Xi,(i∈I}為一族映射.定義映射e:LX→LX如下:
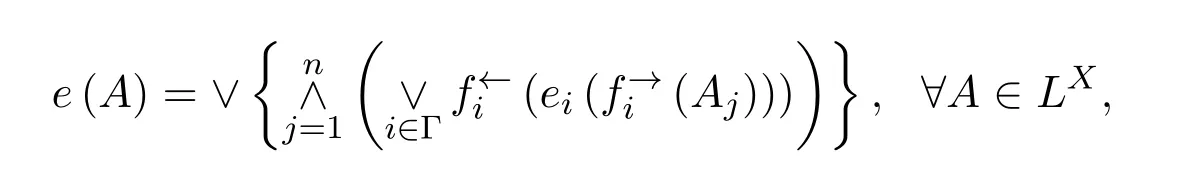
其中第一個∨是對所有滿足條件
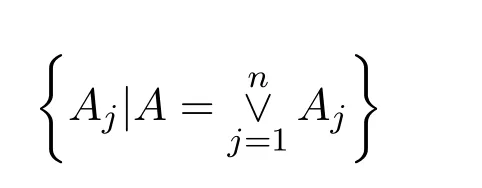
的集族來取的,則下列結論成立:
(1)e是X上使得所有fi(i∈Γ)都連續的最粗的L-外部算子;
(2)若{(Xi,ei)}i∈Γ是拓撲的,e也是拓撲的;
(3)設(Y,e*)為L-外部空間,則映射f:(Y,e*)→(X,e)連續當且僅當?i∈Γ,映射fi?f:(Y,e*)→(Xi,ei)連續.
證明(1)(I)先證e是L-外部算子.
①e(0)=1.任取集族




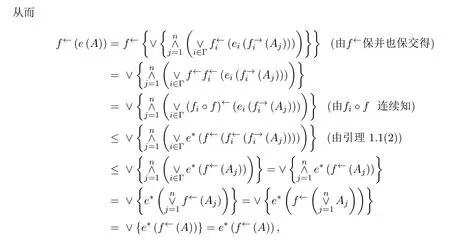
故f連續.
記由L-外部空間和連續映射構成的范疇為L-ES.
定理2.3遺忘函子U:L-ES→SET,U(X,e)=X,U(f)=f是拓撲的.
證明由定理2.2知每一個U-source(fi:X→U(Xi,ei))i∈Γ都有一個唯一的U-初始的提升(fi:(X,e)→U(Xi,ei))i∈Γ,其中e如定理2.2所定義.
由定理2.2和定理2.3得如下定義:
定義2.4設{(Xi,ei)}i∈Γ為一族L-外部空間,X為一集合,fi:X→Xi,(i∈I}為一族映射.X上關于(X,fi,(Xi,ei))(i∈Γ)的初始的L-外部算子結構為使得所有fi都連續的最粗的L-外部算子.
定義2.5設{(Xi,ei)}i∈Γ為一族L-外部空間,
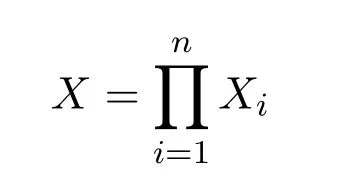
為X1,X2,…,Xn的笛卡爾積.任取i∈I,取fi=pi為投射,稱(X,e)為{(Xi,ei)}i∈Γ的乘積空間,其中e為X上關于(X,fi,(Xi,ei))(i∈Γ)的初始的L-外部算子結構.
定義2.6設(X,e)為L-外部空間,Y?X,idY:Y→X為含入映射.稱(Y,^e)為(X,e)的子空間,其中^e為Y上關于(Y,idY,(X,e))的初始的L-外部算子結構.
推論2.1設{(Xi,ei)}i∈Γ為一族L-預外部空間,X為一集合,fi:X→Xi,(i∈I}為一族映射.定義映射e:LX→LX如下:
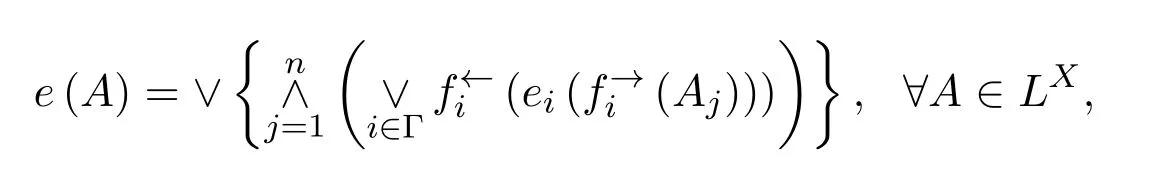
其中第一個∨是對所有滿足條件

的集族來取的.則下列結論成立:
(1)e是X上使得所有fi(i∈Γ)都連續的最粗的L-外部算子;
(2)設(Y,e*)為L-外部空間,則映射f(Y,e*)→(X,e)連續當且僅當?i∈Γ,映射fi?f:(Y,e*)→(Xi,ei)連續.
證明注意到定理2.2的(1)中證明只用到了L-外部算子的逆序性,并未用到其并交性質.同樣,在(3)中也只用到了e的逆序性(當然用到了e*的交并性).
設(X1,e1)為L-預外部算子空間,f1=idX1,e如上面推論所定義,記為c(e1).任取L-外部算子空間(Y,e*)和連續映射f:(Y,e*)→(X1,e),由推論2.1知下圖交換:
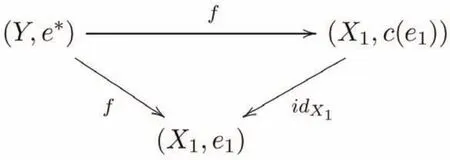
推論2.2L-ES是L-PES(L-預外部空間范疇)的余反射子范疇.
[1]Chang C L.Fuzzy topological spaces[J].JMAA,1986,24(2):37-42.
[2]Y ing Mingsheng.A new app roach for fuzzy topology(I)[J].Fuzzy Sets and System s,1991,39:303-321.
[3]Liu Yingm ing,Luo Maokang.Fuzzy Topology[M].Singapore:World Scientific,1997.
[4]王國俊.L-fuzzy拓撲空間論[M].西安:陜西師范大學出版社,1988.
[5]H¨oh le U,ˇSostak A.Axiomatic foundation of fixed-basis fuzzy topology.In Mathematicsof Fuzzy Sets,Logic, Topology and Measure Theory[M].Boston:K luwer Academ ic Pub lishers,1999.
[6]尤飛.LF-閉包空間及其連通性[J].陜西師范大學學報:自然科學版,2001,29(1):23-29.
[7]K im Yongchan.Initial L-fuzzy closure spaces[J].Fuzzy Sets and System s,2003,133:277-297.
[8]Shi Fugui.L-fuzzy interiors and L-fuzzy closures[J].Fuzzy Sets and System s,2009,160:1218-1232.
[9]韓紅霞,孟廣武.L-保序算子空間的?-緊性[J].純粹數學與應用數學,2009,25(2):390-395.
[10]馬英,孟廣武.外部算子及其應用[J].聊城大學學報:自然科學版,2010,23(4):21-23.
[11]鐘曉靜,蘇華飛,李生剛.用L-預遠域系算子、L-預外部算子或L-預邊界算子確定L-預拓撲[J].模糊系統與數學,2008,22(2):87-91.
[12]賀偉.范疇論[M].北京:科學出版社,2006.
Initial L-exterior spaces
Ma Ying,Li Lingqiang,Meng Guangwu
(Department of Mathematics,Liaocheng University,Liaocheng 252059,China)
The initial L-exterior spaces are discussed.We construct the initial structure of the category of L-exterior spaces,and then define p roduct space and subspace of L-exterior spaces by the initial structure,p rove the category of L-exterior spaces is a coreflective subcategory of the category of L-p reexterior spaces.
L-exterior spaces,L-topological spaces,initial L-exterior spaces
O189.1
A
1008-5513(2012)03-0384-07
2011-02-10.
國家自然科學基金(60875034).
馬英(1986-),碩士生,研究方向:格上拓撲學.
2010 MSC:54A 10

