基于累積指數的電網電壓穩定性能的評估

張學清 梁 軍 董曉明

（山東大學電氣工程學院 濟南 250061）

1 引言

隨著人類生活水平的不斷提高以及社會經濟的持續快速發展，負荷需求種類和數量也不斷地增加；同時電網規模的不斷擴大以及特高壓交直流的廣泛

接入，都給電網穩定與控制帶來了新的挑戰，而如何有效地保持電網的電壓穩定已經成為電網運行與監控的關鍵問題[1]。

傳統電壓穩定性分析主要是利用穩態代數方程的理論，如戴維南等值法[2,3]、連續潮流法[4,5]、靈敏度分析法[6]和模態分析法[7]等。傳統分析方法由于未考慮電網的動態變化過程，尤其是電源與負荷的動態特性，所以有必要考慮電網的動態特性進行電壓穩定性能的評估[8]。近年來，信號能量法已經在機械、動力[9]工程領域得到了廣泛的應用。文獻[10]提出了暫態電壓響應的信號能量，能隨著功率的增加而漸進的增長，并建立了信號能量與傳輸功率和穩定極限的解析函數關系。文獻[11]提出一種基于軌跡識別系統主導振蕩模式的信號能量法，可應用識別多機系統的主要振蕩模式，取得了較好效果。目前在確定地區電網電壓穩定的薄弱節點的研究中考慮過渡過程特性的應用提及較少，并且在現有的網架結構下確定地區電網的電壓薄弱節點對于指導電網的運行和規劃具有一定的意義。

本文提出了一種基于累積指數的電網穩定性能評估的方法。該方法首先利用PSSE的仿真功能得到電網各節點負荷受擾的電壓幅值的信息，由此得出分時段的信號能量譜信息。在此基礎上利用動力學的波動強度理論選取了最佳信號能量波動序列的長度；然后通過構造累積指數判據，確定電網中電壓穩定的薄弱節點。為驗證本文所提方法的可信性，利用傳統電壓分析理論中的PV 曲線法、戴維南等效法[2,12]和本文方法，以山東電網2010年冬的系統運行數據為算例進行對比分析，驗證本文方法的有效性。

2 理論基礎

2.1 分時段信號能量定義

文獻[13]指出，利用系統的時域仿真結果可以提取出在選定母線下的暫態電壓響應信號。由于傳統的基于能量譜的方法沒有考慮到各個負荷節點電壓信號能量沿時間軸的分布特點，有可能導致提取的特征參數不能準確反映暫態信號的特征，所以有必要研究分時段的能量譜理論，分時段能量譜可定義為

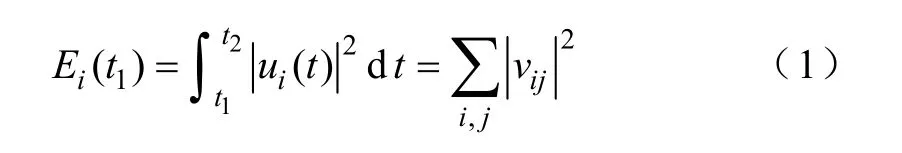
式中，E i(t1)為第i條母線t1時段的信號能量；vij(i=1,…,n;j=1… ,k)為暫態仿真選定第i母線第j時段的電壓幅值。

2.2 波動強度

波動強度[14]（fluctuation intensity）是應用于動力學領域的一種統計物理概念。可以表征信息序列曲線的波動程度，某一段序列波動強度越小，信號波動越小，否則波動越劇烈。

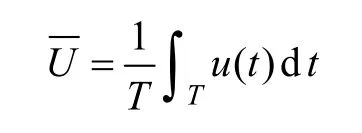
則波動強度數學表達式為

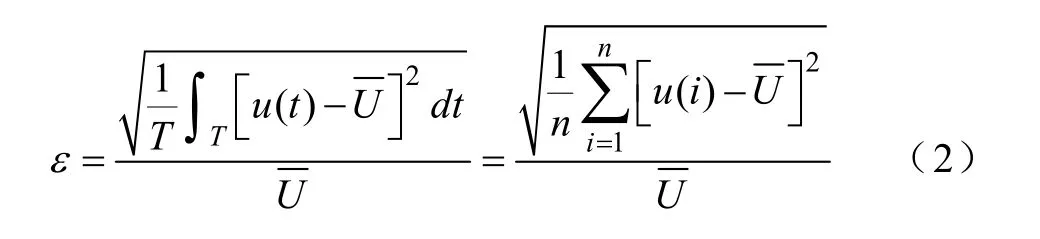
式中，ε表示為波動強度；n為序列的點數；T為采樣周期；u(t)為序列各點值；為這段序列的平均值。

累積指數（cumulating index）是在穩定性理論的超調量和調節時間的思想的指導下利用分時段的信號能量譜概念而得出的，超調量越小、調節時間越短即系統各個負荷節點接受相同的擾動后能恢復穩態的時間越小，那么這個負荷節點也越容易穩定，即此負荷節點穩定性能越好，屬于強節點，反之為弱節點。下面以經典二階系統穩定理論為例說明累積指數方法的有效性。

2.3 經典二階系統階躍響應信號分析

由經典穩定性理論知，系統的穩定性主要由系統特征根的實部決定，而且特征根的實部離虛軸越遠，則所代表的系統更穩定。本文以三個典型的二階系統受到單位階躍響應為例，驗證本文所提方法的有效性，響應曲線如圖1 所示。

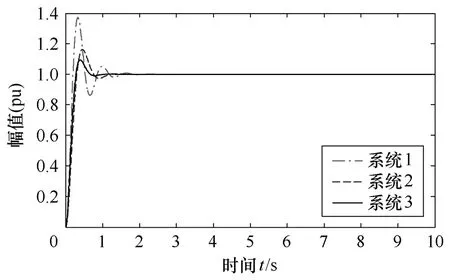
圖1 典型二階系統的階躍響應曲線Fig.1 Typical curve of second-order system step response

由圖1 易見系統3 比系統1 和2 穩定。各系統特征根及累積指數見表1。由表1 知，因為系統3特征根的實部比系統1 和2的實部離虛軸更遠，所以系統3 更穩定。通過系統的超調量和調節時間等性能指標進行對比分析，顯然系統3的超調量和調節時間都大于系統1 和2，由此說明系統3 比系統1和2 穩定。

表1 各系統特征根以及累積指數Tab.1 Eigenvalues and cumulating index of each system

3 累積指數

本文采用分時段能量譜概念，考慮波動強度理論的基礎上給出累積指數（CI）的概念，定義如下

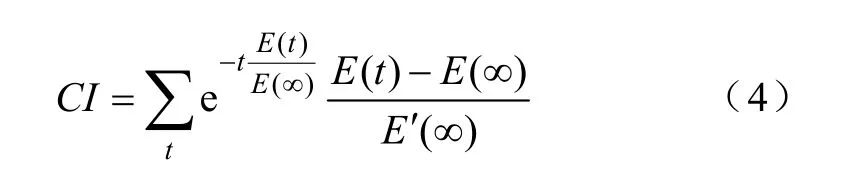
式中，t為仿真的時段；E(t)為第t時間段的信號能量；E′(∞)為受擾信號經過波動強度理論判定為平穩后的時段信號能量；E′(∞)為受擾信號未處理前平穩后的穩態信號能量，如果不經處理，E′(∞)=E(∞)。

累積指數體現了系統超調量和調節時間性能指標的關系，也體現了信號隨時間變化的特征。當系統失穩或者臨界振蕩時，E′(∞)和E′(∞)為零，通過對式（4）求極限易得此極限為無窮大；如果經過一段時間系統平穩，通過計算分析則其有確定的數值，且累積指數越小，穩定性能越好。如果沒有指數部分，將不能體現調節時間的指標思想。其可從整體上反映系統各部分綜合作用的結果[15]，體現了系統自身的性質。

以系統1、2 和3 為例，用累積指數分析如下：從圖1 可以看出，系統1 調節時間比系統2 和3 明顯變長，而且用累積指數計算得出的數值，-0.002 685 9明顯大于-0.039 736 和-0.043 246。這里指數出現了負值，是因為第1 時段與最后的時段的信號能量相比較小，所以出現了負值，但是并不影響累積指數法的成立。但是在電力系統的應用中累積指數很少會出現負值，這是因為隨著擾動過程的持續，系統在各種調節裝置包括發電機、勵磁系統、調速系統以及各種補償裝置等共同的作用下，接近平穩時段的信號能量明顯小于開始受擾瞬間的信號能量，因此，電力系統中基本不會出現指數非負的情況，這從后續分析中可以看出。所以系統1 比系統2 和3穩定性能差，也驗證了累積指數能很好地區分系統的穩定性能的強弱。

對于電力系統來說，通常需要確定電網中的薄弱節點，以利于調度部門對該節點進行重點監控。鑒于此，把累積指數引入到確定電網薄弱節點的分析中，計算電網各個節點的累積指數的大小，累積指數越小，說明此節點的穩定性能越好，如果經受同樣比例的擾動，發生電壓失穩如臨界振蕩，通過對式（4）求極限易得到無窮大，說明已經失穩。且累積指數確定的指標能隨擾動大小的不同而不發生變化，所以累積指數能用于評估電力系統節點電壓穩定性能的強弱。

4 算例分析

本文以山東電網2010年冬季孤網運行方式為例驗證本文方法的有效性。2010年冬季，山東電網由河北辛安站以及廉州站，受電4 000MW。寧東直流單極運行（膠東站）受電2 000MW。

4.1 算例仿真

在山東電網2010年冬季孤網運行方式下，用山東電網整個大區域作為本文算例。為了節約篇幅，以山東濰坊受電區域的節點結果展示為例，運用累積指數法確定電網的薄弱節點。部分受電區域圖如圖2 所示。

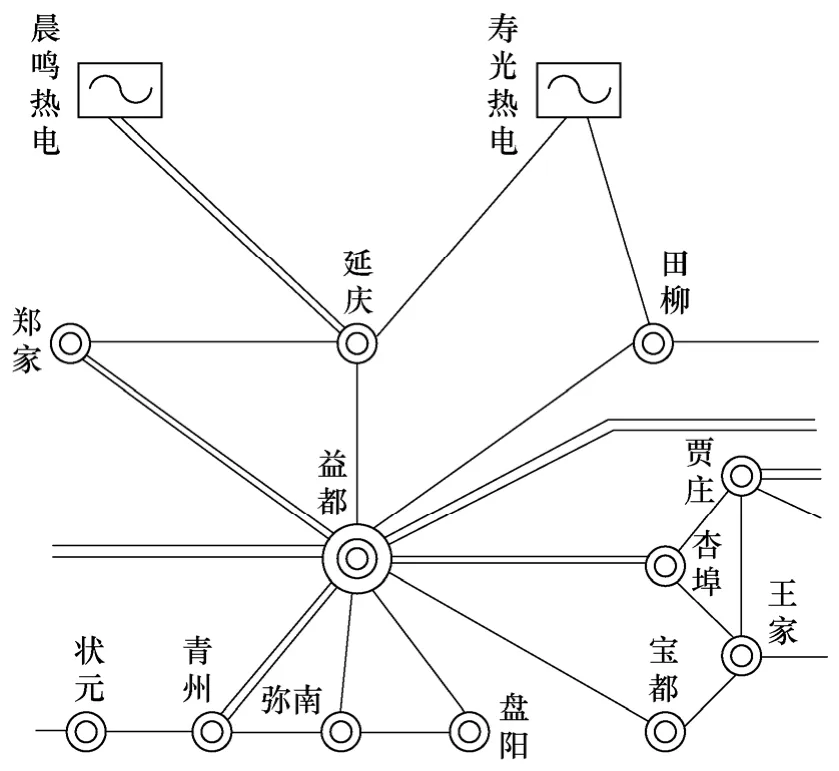
圖2 山東電網濰坊受電區域圖Fig.2 Electrical map of Weifang in Shandong grid

圖2 中濰坊地區11 個負荷節點都用三繞組變壓器與輸電系統關聯，其中三繞變模型的220kV 側接輸電線路，110kV 側接等效負荷，35kV 側接補償裝置。以原山東電網全網各負荷節點的功率因數增沖擊負荷，在PSSE 中仿真了山東電網各個負荷節點的電壓幅值變化情況。本文首先利用PSSE的潮流計算模塊FNSL 計算了山東電網的各節點的電壓幅值和相角，并以此為基礎利用PSSE的STRT，RUN等模塊仿真了山東電網各個節點的電壓變化情況。發電機采用的是PSSE的經典5 階模型GENSAL，勵磁模型采用的是自定義模型，調速系統采用了PSSE的IEEEG1 模型，負荷模型采用的是PSSE的綜合負荷CLOD 模型，直流輸電部分采用CDC6T模型。仿真的具體情況是從0 開始仿真各個負荷節點的電壓幅值，運行到1s 時，突然全網按照各節點的功率因數增1%的沖擊有功和無功負荷，運行到4s 時再按照全網各節點的功率因數增2%的沖擊有功和無功負荷，仿真到第29s 結束。濰坊地區的部分220kV 負荷節點的電壓幅值變化情況如圖3 所示。

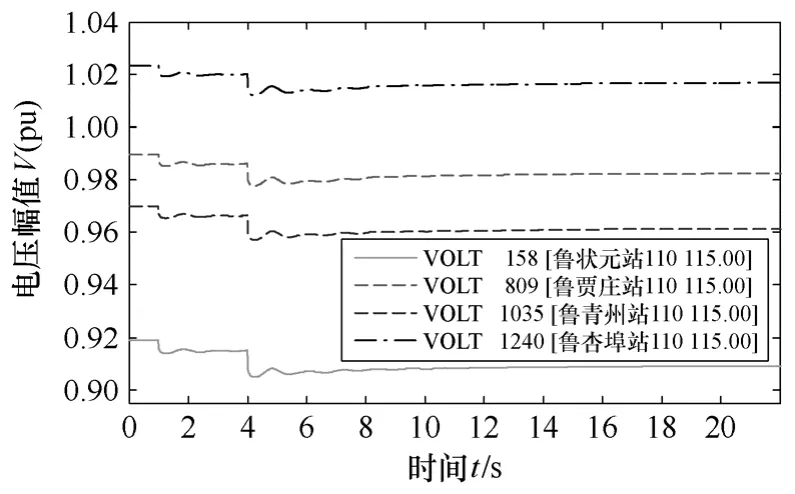
圖3 濰坊受電區域部分負荷節點的電壓幅值變化曲線Fig.3 Voltage magnitude curve of load node in Weifang zone

應用暫態信號判斷系統各個節點的電壓穩定程度的強弱，常規的方法是利用各負荷節點的電壓初值以及受擾過程中電壓跌落的最小值來判斷節點受擾的強弱。這種方法是有局限性的，其沒有考慮受擾之后相當長時間內信號的變化情況以及受擾恢復之后的電壓變化情況，而累積指數方法則綜合考慮了這些因素。為了應用累積指數，本文進行了如下的處理。由于各個負荷節點初始電壓各不相同，而且受擾之后達到穩態時電壓幅值也不相同，本文將各個負荷節點的電壓初始情況統一歸算到相同的電壓初始值，即對每一個負荷節點的電壓幅值向量減去它們的初始值電壓幅值組成的向量，并且第一個時段就是從最后一個受擾開始時刻即仿真的第4s 開始的，其后依此類推，其中式（4）中分母的穩態時段能量仍采用歸算前表示形式并除以1 000，這樣可以保證如果某一節點發生電壓失穩，穩態能量為零，指數為無窮大表明系統失穩。濰坊地區部分負荷節點前10 個時段信號能量見表2。

4.2 最佳信號序列長度的確定

確定電網各個節點的電壓穩定程度的強弱，首先需要確定最佳波動序列的長度。前面提到的波動強度理論可以表征信號序列波動程度，所以通過對仿真得到的全網各節點按各自的功率因數遞增相同的有功和無功負荷的電壓幅值波動曲線分別計算每一時段的波動強度值，再把該區域中的所有負荷節點的波動強度數值用曲線聯系起來，得到如圖4 所示的各負荷節點的波動強度。從圖3 可以看到，所有的負荷節點的波動強度曲線在第17 個時段基本維持平穩，即到第17 個時段時的信號序列已能很好地表征信號的主要特征，為計算方便這里將第 21個時段以前的序列作為本文分析電壓波動信號，這樣能保證不遺漏有用的信息。

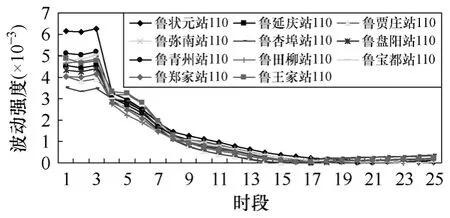
圖4 濰坊受電區域各負荷節點的波動強度變化曲線Fig.4 Fluctuation intensity curve of load node in Weifang

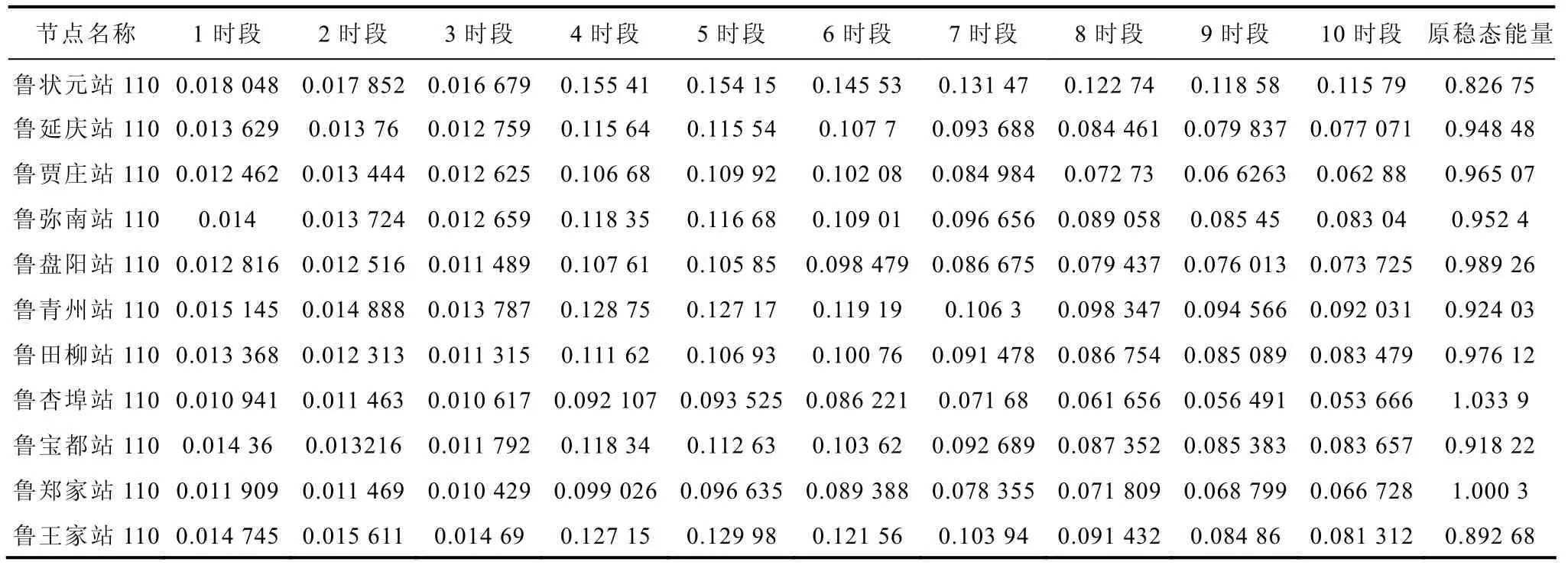
表2 濰坊地區負荷節點的各時段信號能量Tab.2 Signal energy of each time for load node in Weifang

各個負荷節點的累積指數數值見表3。從表3可見，濰坊地區魯狀元110kV 站指數最大，所以此負荷節點電壓穩定性能較差，為此區域的薄弱節點，而此地區的魯杏埠110 站指數最小，所以此負荷節點電壓穩定能較好，為此受電區域的強節點。本文還仿真了另一組負荷擾動即從0 開始仿真各個負荷節點的電壓幅值，運行到1s 時，突然全網按照各節點的功率因數增2%的沖擊有功和無功負荷，運行到4s 時再按照全網各節點的功率因數增4%的沖擊有功和無功負荷，仿真到第29s 結束。濰坊地區的220kV 部分負荷節點的累積指數數值見表4。通過表4 可見，薄弱節點仍是狀元站和青州站，指數數值相對較大，而強節點仍是賈莊110 站和杏埠110站，指數數值相對較小。而且表4的排列順序與表3 完全一致，說明由累積指數確定的節點電壓穩定性能評估排序結果不隨擾動的大小而變化，具有很好的一致性，且說明負荷節點穩定性能的強弱不因擾動大小而變化，而是由系統本身的結構決定的，即全網各部分包括網架結構和控制裝置綜合作用的結果。

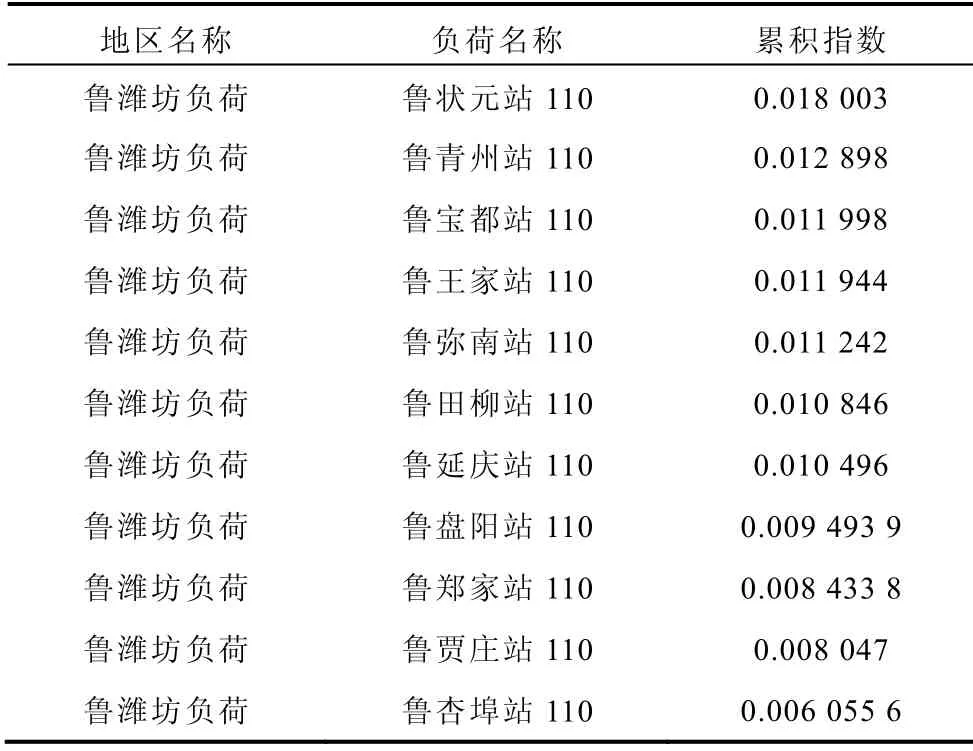
表3 濰坊地區各負荷節點累積指數Tab.3 Cumulating index of each load node in Weifang

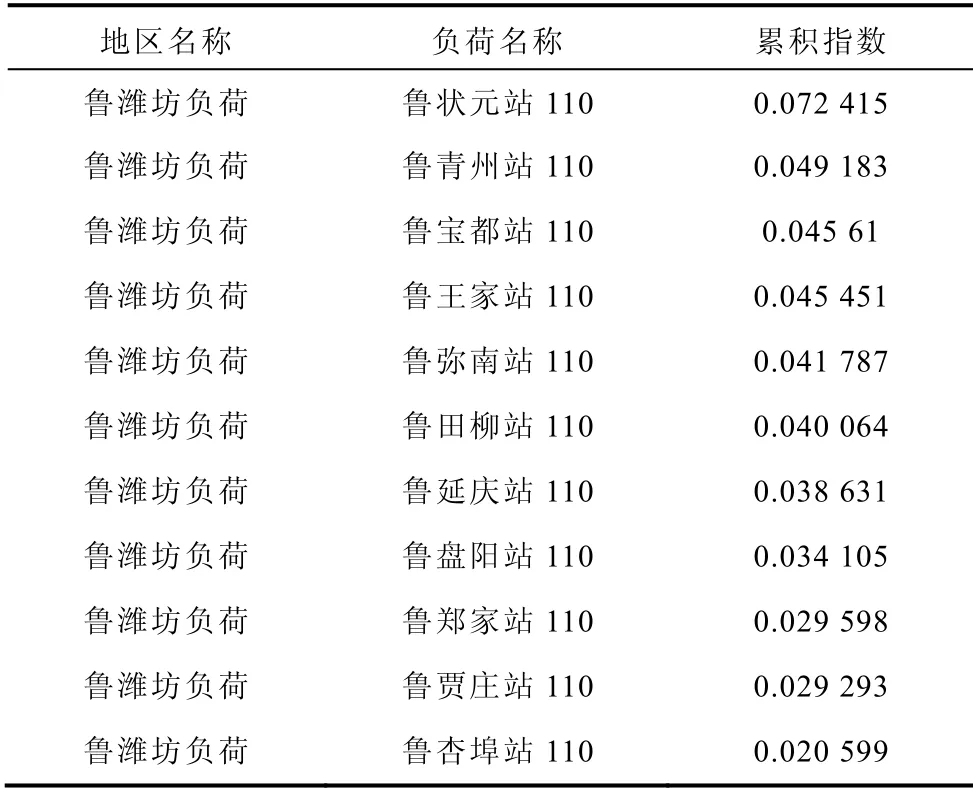
表4 濰坊地區各負荷節點累積指數Tab.4 Cumulating index of each load node in Weifang

5 傳統分析方法驗證

為了驗證本文方法的有效性，鑒于傳統分析方法應用在電壓穩定分析中已經很多，在此利用傳統分析方法中的PV 曲線法[4,5,8]和戴維南等效法[16-18]來驗證濰坊地區的薄弱節點。

5.1 連續潮流（PV 曲線）法

設計功率增長模式為單個負荷節點保持功率因數緩慢增長，由虛擬的華北平衡機提供不平衡功率增長，直至靜態電壓穩定臨界點。

忽略發電機出力限制、節點電壓、線路熱電流等約束條件，僅考察網絡的極限功率輸送能力。結果見表5。表中λ為臨界功率與基準點功率比值。

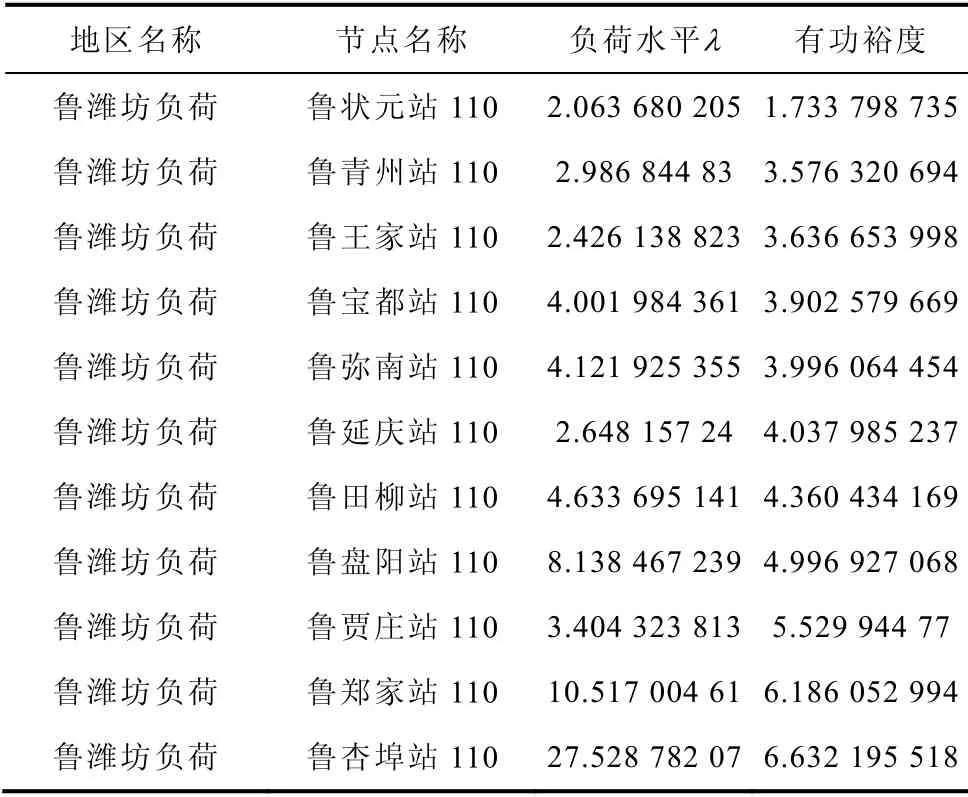
表5 負荷節點的臨界電壓幅值指標Tab.5 Threshold voltage amplitude index of load node

5.2 戴維南等效法

具體實現方法是，將辛安站以及廉州站統一等值為華北平衡機，作為平衡節點處理。并將直流部分等值為一臺定出力發電機，以PQ 節點處理。山東電網冬季大方式下，在全網發電和負荷初始值基礎上，各自功率因數遞增一小的量（類似平衡點線性化處理），得到兩個潮流數據斷面，進而求得各節點戴維南等效參數，具體參見文獻[16]。本文用到的三個指標，即阻抗指標、功率指標以及角度指標，具體見文獻[3,12,18]。在以上三個指標的基礎上對每一個負荷節點通過求三個指標之和的平均值得到的平均指標的概念去確定山東濰坊受電區域節點電壓穩定強弱的排列順序，結果見表6。

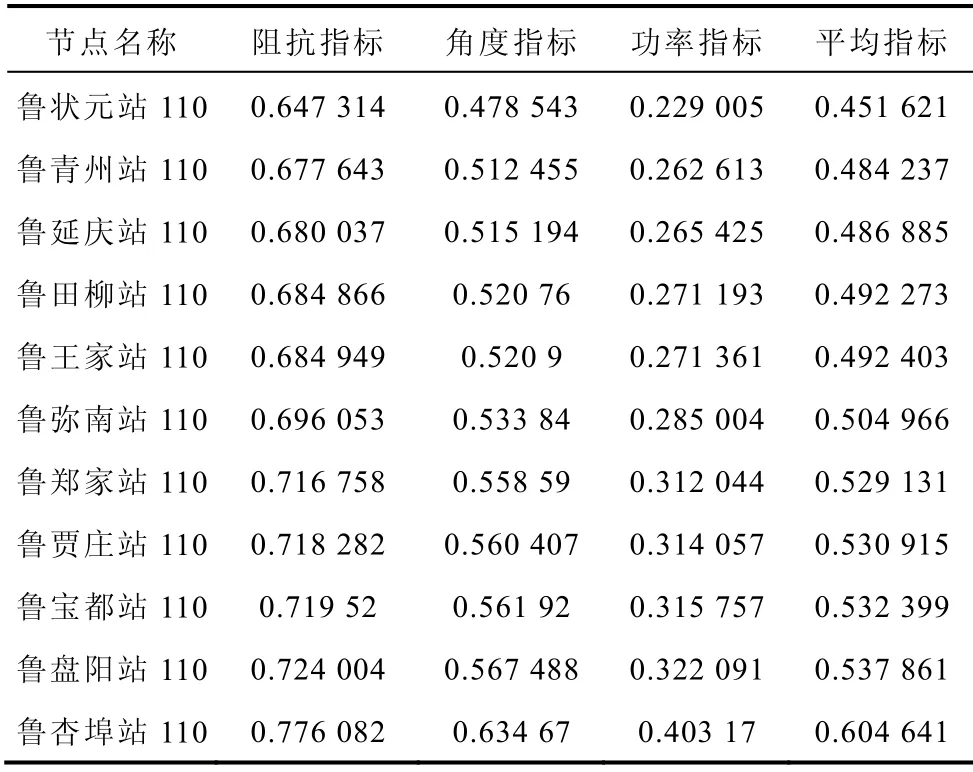
表6 負荷節點的各種裕度指標Tab.6 Each margin index of load node

對比表3、表5 和表6 可知，PV 曲線法分析結果表明狀元站、青州站、王家站和寶都站都是相對弱節點，而累積指數法結果表明狀元站、青州站、寶都站和王家站為弱節點，而戴維南等效法分析結果也表明狀元站和青州站為較弱節點，可見傳統分析方法與累積指數結果基本一致。雖然部分節點有些許差別，但是大體趨勢與PV 曲線法基本一致。出現此種情況的原因是，本文考慮了發電機、勵磁和調速系統、直流控制系統和各種負荷動態模型得出的結論，而傳統電壓分析沒有考慮各種元件的詳細模型，主要基于穩態的代數方程理論，沒有考慮過渡過程內的變化情況；傳統分析方法負荷增長是緩慢的，忽略了過渡過程中有用的快速變化信息。所以兩種計算有偏差，但是大體趨勢一致，就是戴維南等效法結果中杏埠站的平均指標明顯大于本文累積指數計算出來薄弱節點狀元站和青州站的平均指標。本文采用了沖擊負荷連續擾動的形式，而沒有采用直流閉鎖以及短路等擾動形式就是為了分析在現有的網架結構和控制裝置的作用下電網各節點的電壓穩定性能的強弱。所以用傳統分析方法也驗證了本文方法的有效性。

6 結論

本文針對電力系統電壓穩定性能評估中如何在現有的網架結構下確定電網中電壓穩定薄弱節點這一問題，借鑒系統的超調量和調節時間等性能指標，在信號能量法的基礎上結合分時段信號能量譜提出了累積指數法。針對山東電網2010年冬典型運行方式下用PSSE 仿真了系統按原功率因數連續增沖擊負荷擾動下濰坊受電區域各負荷節點的電壓幅值變化情況，并用累積指數法確定了電網的薄弱節點，并證明了累積指數確定的節點電壓穩定性能評估排序結果能不隨擾動的大小而變化。最后用傳統電壓分析法驗證了本文所提方法的有效性，本方法適用于離線靜態電壓穩定評估，而且計算迅速，可為在現有網架結構下進行電網的運行與規劃提供參考，有一定的工程意義。而利用累積指數法對薄弱節點進行穩定裕度分析的問題還有待于做進一步的深入研究。

[1]薛禹勝.時空協調的大停電防御框架(二):廣域信息、實時量化分析和自適應優化控制[J].電力系統自動化,2006,30(2):1-10.Xue Yusheng.Space-time cooperative framework for defending blackouts,part Ⅱ:reliable information quantitative analyses and adaptive controls[J].Automation of Electric Power Systems,2006,30(2):1-10.

[2]柳焯.基于節點阻抗解析的電壓穩定性預估[J].中國電機工程學報,1999,19(11):64-68.Liu Zhuo.Voltage stability evaluation based on node load impedance analyses[J].Proceedings of the CSEE,1999,19(11):64-68.

[3]劉道偉,韓學山,王勇,等.在線電力系統靜態穩定域的研究及其應用[J].中國電機工程學報,2009,29(34):42-49.Liu Daowei,Han Xueshan,Wang Yong,et al.Studies on the on-line static stability region in power systems and its application[J].Proceedings of the CSEE,2009,29(34):42-49.

[4]趙晉泉,黃文英,方朝雄,等.福建電網在線電壓穩定監視與控制系統(VSMC)[J].電力系統自動化,2007,31(14):102-106.Zhao Jinquan,Huang Wenying,Fang Zhaoxiong,et al.Fujian on-line voltage stability monitoring and control system[J].Automation of Electric Power System,2007,31(14):102-106.

[5]趙晉泉,王毅,李可文,等.一種基于連續潮流的在線靜態穩定綜合評估方法[J].電力系統自動化,2010,34(4):18-22.Zhao Jinquan,Wang Yi,Li Kewen,et al.An on-line voltage stability composite assessment method based on continuation power flow[J].Automation of Electric Power Systems,2010,34(4):18-22.

[6]段獻忠,何仰贊,陳德樹.論電力系統電壓穩定幾種實用判據和安全指標[J].電力系統自動化,1994,18(9):36-41.Duan Xianzhong,He Yangzan,Chen Deshu.On some practical criteria and security indices for voltage stability in electric power system[J].Automation of Electric Power Systems,1994,18(9):36-41.

[7]Taylor C W.Power System Voltage Stability[M].New York:McGraw-Hill,1994.

[8]王錫凡,方萬良,杜正春.現代電力系統[M].北京:科學出版社,2003.

[9]周云龍,陳飛,孫斌.基于圖像小波包信息熵和遺傳神經網絡的氣-液兩相流流型識別[J].核動力工程,2008,29(1):115-119.Zhou Yunlong,Chen Fei,Sun Bin.Identification method of gas-liquid two-phase flowregime based on image wavelet packet information entropy and genetic neural network[J].Nuclear Power Engineering,2008,29(1):115-119.

[10]Marceau R J,Soumare S.A unified approach for estimating transient and long-term stability transfer limits[J].IEEE Transaction on Power Systems,1999,14(2):693-701.

[11]穆鋼,王宇庭,安軍,等.根據受擾軌跡識別電力系統主要振蕩模式的信號能量法[J].中國電機工程學報,2007,27(19):7-11.Mu Gang,Wang Yuting,An Jun,et al.Signal energy method for identification of main oscillation mode in power system based on disturbed trajectory[J].Proceedings of the CSEE,2007,27(19):7-11.

[12]汪洋,盧繼平,李文沅,等.基于局部網絡電壓相量的等效模型及其電壓穩定性指標[J].中國電機工程學報,2008,28(34):52-59.Wang Yang,Lu Jiping,Li Wenyuan,et al.An Equivalent model and voltage stability index based on local network voltage phasors[J].Proceedings of the CSEE,2008,28(34):52-59.

[13]金敏杰,陳家榮,梅生偉,等.基于改進信號能量法估計暫態穩定極限[J].中國電機工程學報,2004,24(19):1-6.Jin Minjie,Chen Jiarong,Mei Shengwei,et al.Transient stability limit assessment by modified signal energy approach[J].Proceedings of the CSEE,2004,24(19):1-6.

[14]李紅智,羅毓珊,王海軍,等.圓弧型與X 型開縫翅片空氣側流動與傳熱特可視化試驗[J].化工學報,2008,59(8):1936-1941.Li Hongzhi,Luo Yushan,Wang Haijun,et al.Visualization experiments on air side heat transfer and fluid flow characteristics of arc-type and X-type slotted fin surfaces[J].Journal of Chemical Industry and Engineering,2008,59(8):1936-1941.

[15]張學清,梁軍,劉道偉,等.基于信號能量綜合指數的電網電壓穩定性能分析[J].電力系統保護與控制,2012,40(12):88-94.Zhang Xueqing,Liang Jun,Liu Daowei,et al.Study of power grid voltage stability based on signal energy aggregate index[J].Power System Protection and Control,2012,40(12):88-94.

[16]湯涌,孫華東,易俊,等.基于全微分的戴維南等效參數跟蹤算法[J].中國電機工程學報,2009,29(13):48-53.Tang Yong,Sun Huadong,Yi Jun,et al.Tracing algorithm for thevenin equivalent parameters based on complete differential equation[J].Proceedings of the CSEE,2009,29(13):48-53.

[17]周雙喜,朱凌志,郭錫玖,等.電力系統電壓穩定性及其控制[M].北京:中國電力出版社,2003.

[19]Corsi S,Taranto G N.A real-time voltage instability identification algorithm based on local phasor measurements[J].IEEE Transactions on Power Systems,2008,23(3):1271-1279.