晶閘管可控電抗器的諧波產生特性研究

孫媛媛 尹志明 鄭偉杰 劉 穎

（1.山東大學電氣工程學院 濟南 250061 2.中國電力科學研究院 北京 100192 3.山東電力集團濟南供電公司 濟南 250021）

1 引言

晶閘管可控電抗器（Thyrisor Controlled Reactors，TCRs）由兩個反并聯的晶閘管串聯一個電抗器組成，它是靜止無功補償中的重要組成元件[1]。TCRs作為可變電感，可快速、平滑地調節所吸收的無功功率，因此它和晶閘管投切電容器（Thyristor Switched Capacitor,TSC）一起成為電力系統中無功補償和電壓調節的重要手段[2,3]。然而，從電能質量方面考慮，TCRs 作為開關型電力電子器件，在運行過程中，將大量的諧波電流注入系統，是電力系統中重要的非線性諧波源[4,5]。

分析 TCRs 產生的諧波，主要有四類方法。①恒流源法：基于TCRs的典型諧波頻譜和特定運行工況的基波潮流結果，根據恒流源法的公式計算得出TCRs 注入系統的諧波電流[6-8]，該方法在目前的諧波分析中應用廣泛。②諾頓等效電路模型：在恒流源模型的基礎上并聯表征TCRs 諧波電壓和諧波電流自耦合效應的導納[9,10]，但未考慮諧波電壓和諧波電流之間的互耦合作用。③基于傳遞函數的模型：TCRs 中背靠背的晶閘管交替導通和關斷，任一晶閘管導通時定義開關函數為1，所有晶閘管都關斷時定義開關函數為0[11-13]；基于此傳遞函數，在頻域中推導得出TCRs的諧波模型[14]。該模型通過兩個導納矩陣將TCRs 各次諧波電壓和諧波電流的耦合關系展示出來，模型準確但計算復雜。④時域法：用微分方程描述TCRs 電壓和電流之間的關系，通過求解微分方程得出TCRs 注入系統的諧波電流[15]。該方法準確，但對大系統來說，搭建模型所需的工作量大且仿真運行時間長。

以上各諧波模型的提出均以在諧波潮流中應用為主，缺乏對TCRs 諧波特性的分析。而研究TCRs的諧波產生特性，將有助于對諧波源建模采取合理的近似和簡化以及諧波潮流分析的進行。頻域中TCRs的諧波矩陣模型[14]通過完全解析的公式將TCRs 端口各次諧波電壓和諧波電流之間的耦合關系直觀地展示出來。本文將基于TCRs的諧波耦合矩陣模型，對TCRs的諧波產生特性進行深入分析。研究發現，TCRs的每次諧波電流均由三部分組成：由基波電壓產生、由同次諧波電壓產生以及由不同次諧波電壓的耦合作用產生的諧波電流。本文首先分析了諧波電流各組成部分的貢獻大小，在此基礎上提出了TCRs的忽略諧波電壓共軛影響的模型、解耦的模型和恒流源模型，給出了各簡化模型的解析計算公式，并研究了觸發延遲角對簡化模型精度的影響。

2 TCRs的諧波耦合矩陣模型

TCRs 多按三角形聯結方式在三相電路中使用，如圖1 所示。3 及3的倍數次諧波經三相電感環流而不注入交流系統。

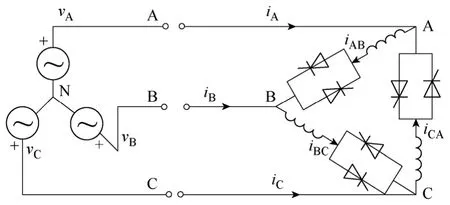
圖1 三相三角形聯結TCRs的電路圖Fig.1 Circuit of three phase delta connection TCRs

根據三相TCRs的工作原理和傳遞函數，可在頻域中推導出其諧波耦合矩陣模型[14]

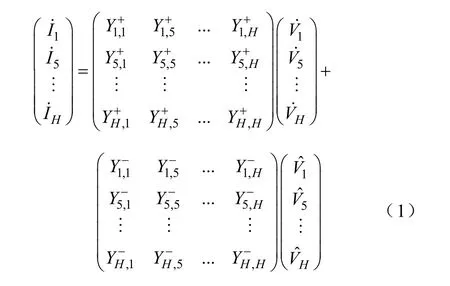
式中，h=1,5,7,…,H，H為所計算的諧波最高次數，和分別為TCRs 端口的h次諧波電流和電壓相量，為的共軛分量，Y+和Y-是TCRs的諧波耦合矩陣模型。矩陣各元素的解析表達式為

式中，α為晶閘管的觸發延遲角；L為TCRs 中的電抗值。

模型表明，TCRs的諧波電流不僅由其端口的諧波電壓產生，而且也與其諧波電壓共軛分量有關。該模型將TCRs 端口的諧波電壓和它所產生的諧波電流之間的耦合關系通過Y+和Y-兩矩陣直觀地體現出來，且矩陣的各元素以完全解析的公式給出。通過分析諧波耦合矩陣元素的特點，可對TCRs的諧波產生機制進行分析。

3 TCRs的諧波耦合矩陣特性分析

首先給出Y+、Y-各元素相對大小的直觀比較（見圖 2，觸發延遲角為 20°）。所有元素均以（幅值最大的元素）為基準進行標幺化，對比結 果以百分比的形式給出。由圖可知，Y+的對角線元素、第一行、第一列以及Y-的第一行元素有較大的幅值，說明這些元素所對應的電壓分量在TCRs的諧波電流產生中起主要作用。

3.1 基波電壓的作用

Y+、Y-的第一列元素共同表征了TCRs 端電壓的基波分量對TCRs 各次諧波電流產生的影響。因Y-的第一列元素為零，該影響完全由Y+的第一列元 素決定。由式（2）可知，的幅值有如下形式：

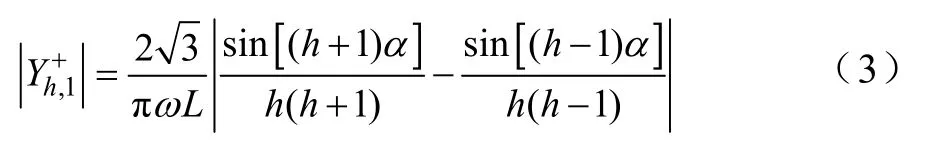
式中，sin ［(h+1)α］的取值在（0,1）的范圍內；的幅值隨諧波電流次數h的增大，以的速度遞減。如果供電電源中不含諧波，TCRs 產生的諧波電流隨諧波次數減小的速度將大于整流裝置[13]。

由式（3）可知，任一元素幅值均是觸發延遲角的函數，圖3 示出了隨觸發延遲角和諧波次數的變化規律（所有元素均以為基準進行標幺化）。這一列元素不含任何諧波的作用，是恒流源模型的解析計算公式。因此可將式（1）所示的完整模型分為基波電壓（恒流源模型，）與諧波電壓的作用兩部分，如式（4）所示。

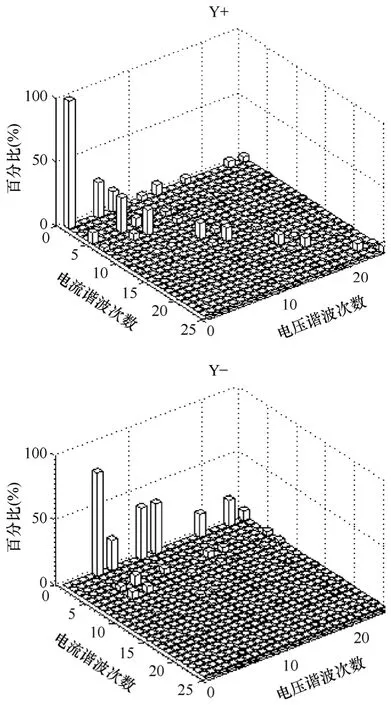
圖2 Y+、Y -矩陣元素幅值相對大小對比圖（觸發延遲角20°）Fig.2 Elements relative amplitude comparison for Y+and Y-when the firing angle is 20°

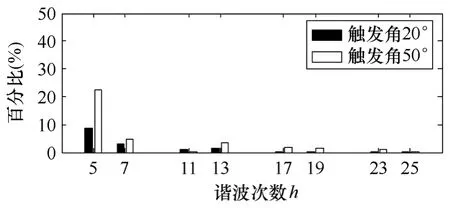
圖3 Y+矩陣第一列元素幅值隨觸發延遲角的變化規律Fig.3 The amplitude variation of Y+first column elements with firing angle

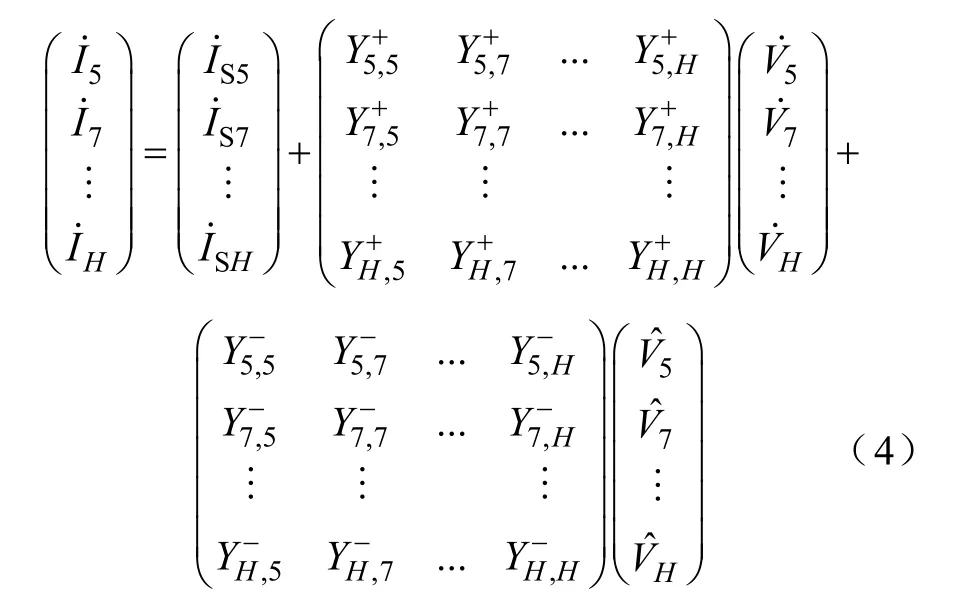
3.2 諧波電壓對基波電流的作用

TCRs的基波電流主要由基波電壓通過1,1Y+產生（1,1Y+即為TCRs 基頻下的等效導納），但Y+和Y-的第一行均有非零元素，表明TCRs 將供電端的部分諧波電壓轉化為基波電流送入系統。元素的幅值為

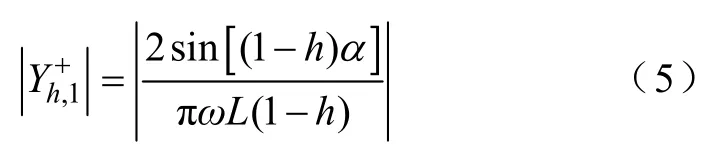
該幅值隨諧波次數的增大以1h的速度遞減。圖 4所示為了元素幅值隨觸發延遲角和諧波電壓次數的變化規律。研究發現，隨觸發延遲角的增大，并不總是第一行中幅值最大的元素，如當α=70°時，成為幅值最大的元素。但從電力系統實際考慮，單次諧波電壓畸變率一般小于5%，因此該轉化作用對基波潮流的影響不大。

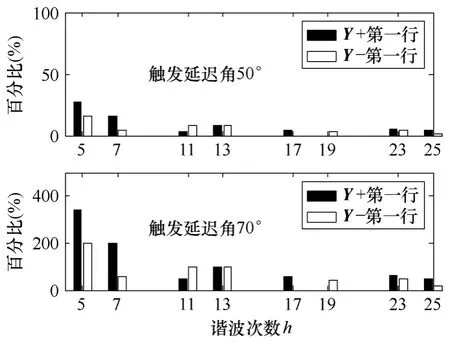
圖4 Y+、Y -第一行元素幅值隨觸發延遲角和諧波電壓次數的變化規律Fig.4 The variation of Y+and Y -first row elements amplitude with harmonic voltage order and firing angles

3.3 TCRs的諧波自導納

Y+對角線元素表征h次諧波電壓與h次諧波電流之間的自耦合效應，即TCRs的諧波自導納，計算公式如下：

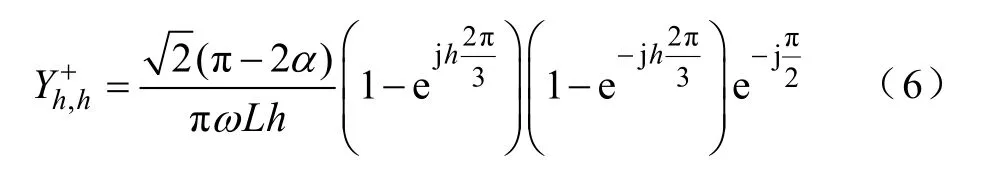
推導發現，對角線元素的幅值以1/h的速度遞減，與值為的電抗具有相同的特性，表明TCRs 在諧波頻率下等值為的感 性電抗。但該值與TCRs 在基頻下的電抗并不相同。由式（2）可知，基頻下TCRs的電抗值L1為

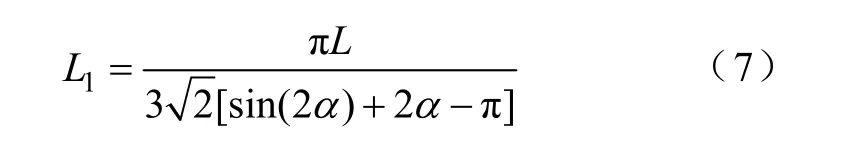
式（6）和式（7）可作為TCRs 諾頓等效電路模型中自導納的修正公式[10]。

3.4 諧波電壓與諧波電流的互耦合

TCRs 諧波電壓與諧波電流之間的互耦合效應，即某次諧波電壓對另外一次諧波電流的影響，可由分析Y+的非對角線元素得出。Y+的非對角元素幅值為

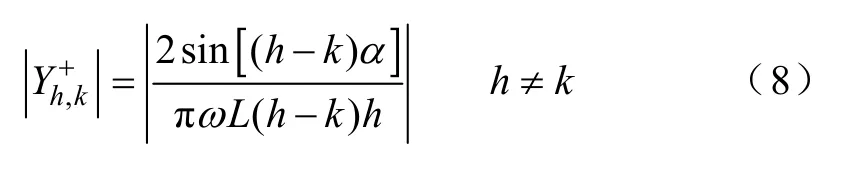
元素的幅值隨諧波次數h的增大而遞減，同時 元素還隨遞減。是h次諧波電壓與k次諧波電流之間的距離，距離越近，越大。為衡量互耦合作用的強弱，定義參數K+為

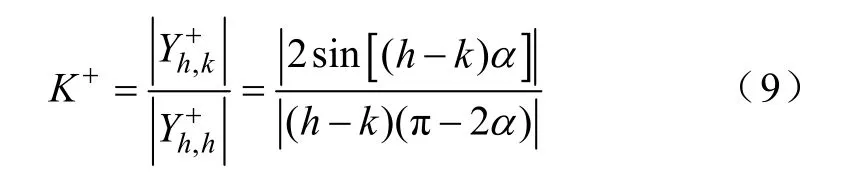
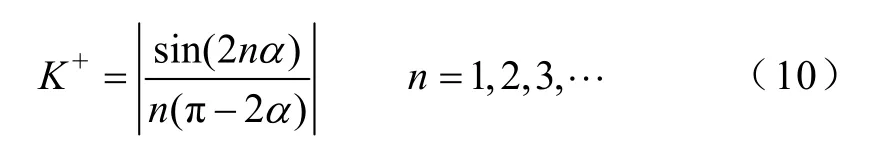
K+隨兩耦合諧波次數的距離而變化，同時也隨觸發延遲角α變化，其變化規律如圖5 所示。

分析式（9）和圖5 可得出以下結論：

（1）對于h次諧波電流，（h-k）次諧波電壓對其產生的影響與（h+k）次諧波電壓產生的影響具有相同的幅度。

（2）對任意觸發延遲角α和組合，K+總小于1，即在Y+矩陣的任一行（h＞1），對角線元素總是幅值最大的元素。

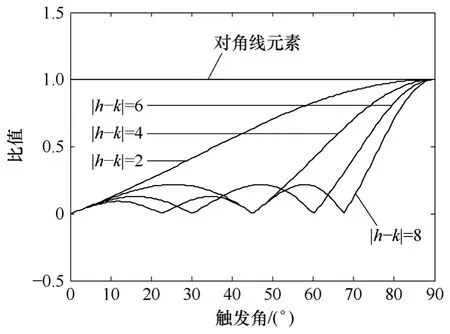
圖5 Y+矩陣非對角線元素與對角線元素的比值隨觸發延遲角的變化規律Fig.5 The ratio variation of Y+non-diagonal elements to the diagonal elements amplitude with the firing angles

（4）當觸發延遲角接近90°時，K+接近1，此時對角線元素變得非常小（見式（2）），所以TCRs的諧波耦合作用是很弱的。

3.5 諧波電壓共軛的貢獻大小研究

為研究TCRs 端口諧波電壓共軛對其諧波電流產生的影響，定義K-為Y-元素與Y+對角線元素幅值之比

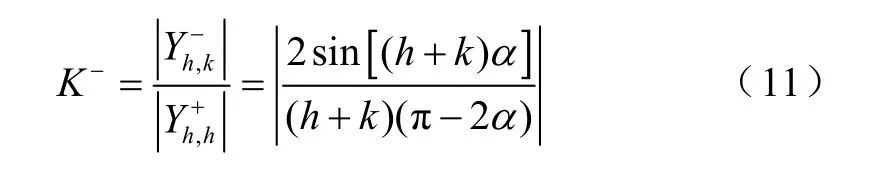
K-隨諧波電壓和諧波電流次數之和變化，當k=h=5 時,取得最小值。圖6 為K-隨觸發延遲角的變化規律。可見，K-比K+更小。 觸發延遲角α≤60°時，K-小于0.2。這表明，TCRs供電端電壓的共軛分量在TCRs 諧波電流產生中的作用要遠小于其端電壓相量。

圖6 Y-矩陣元素與Y+對角元素的比值隨觸發延遲角的變化規律Fig.6 The ratio variation of Y-elements amplitude to the Y+diagonal elements amplitude with the firing angles

4 TCRs的諧波分析簡化模型

通過以上對TCRs 諧波耦合矩陣元素的取值規律和物理意義的分析，得出TCRs的諧波產生有如下特點：

（1）Y+第一列元素表征TCRs 端電壓基波分量對TCRs 諧波電流產生的影響。此列元素不含任何諧波電壓的作用，是恒流源模型的計算公式。

（2）Y+對角線元素總是每行中幅值最大的（h＞1），且離對角線越近的非對角線元素幅值越大。這表明，對任一次諧波電流，同次諧波電壓與其產生的自耦合效應要強于不同次諧波電壓與其的互耦合效應，互耦合的程度隨諧波電壓和諧波電流距離的增大而減小。

（3）TCRs 供電端電壓的共軛分量對TCRs 諧波電流產生的作用遠小于其端電壓相量。

基于諧波耦合矩陣元素的取值規律以及 TCRs的諧波產生特性，可對TCRs的諧波模型進行簡化。

（1）Y+模型：忽略諧波電壓共軛對各次諧波電流產生的影響

（2）解耦模型：在Y+模型的基礎上，進一步忽略Y+的非對角線元素，即忽略諧波電壓和諧波電流的互耦合作用，并將基波電壓對諧波電流產生的影響表示為恒流源

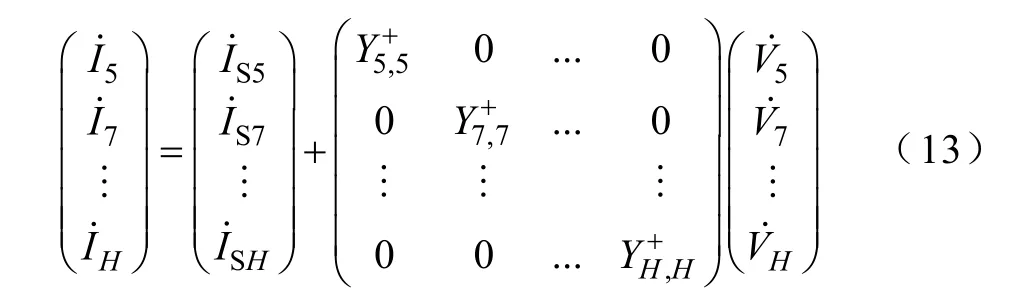
（3）恒流源模型：在解耦模型的基礎上，進一步忽略各次諧波電壓和諧波電流之間的自耦合效應，只考慮基波電壓的影響，可得出TCRs的恒流源模型，其諧波電流的解析計算公式與式（13）中的相同。恒流源模型由于計算簡單方便，是目前各類諧波分析中廣泛采用的模型。

5 觸發延遲角對簡化模型精度的影響

由式（2）可知，任一元素均是觸發延遲角α的函數，觸發延遲角將影響各簡化模型的精度。根據TCRs的運行機理，α在0～90°范圍內變化。當系統的供電電壓總畸變率為9.68%時，對各模型的精度進行了分析（Matlab Simulink 仿真電路參數見表1）。圖7 給出α為10°、40°、80°時，各簡化模型與精確模型的仿真波形結果對比。

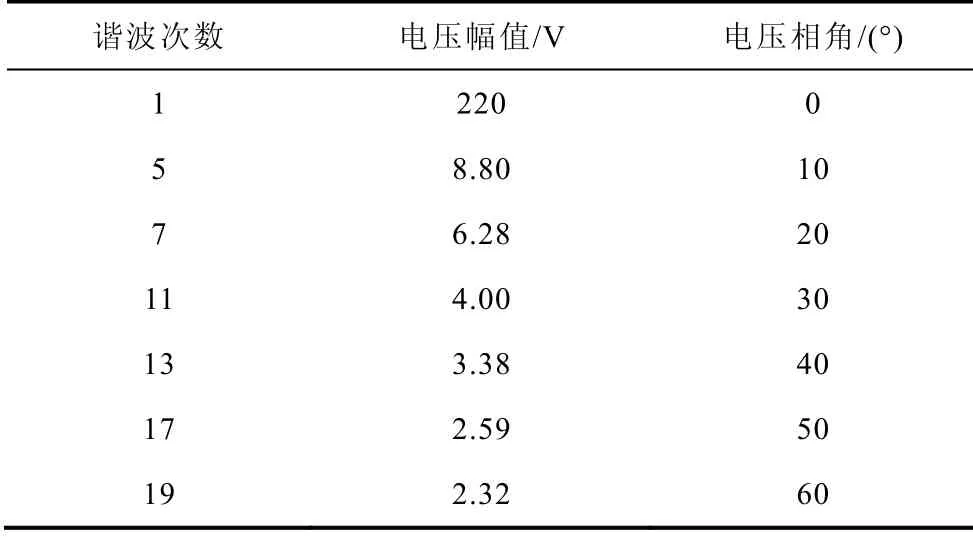
表1 仿真電路參數Tab.1 Parameters for the simulation models

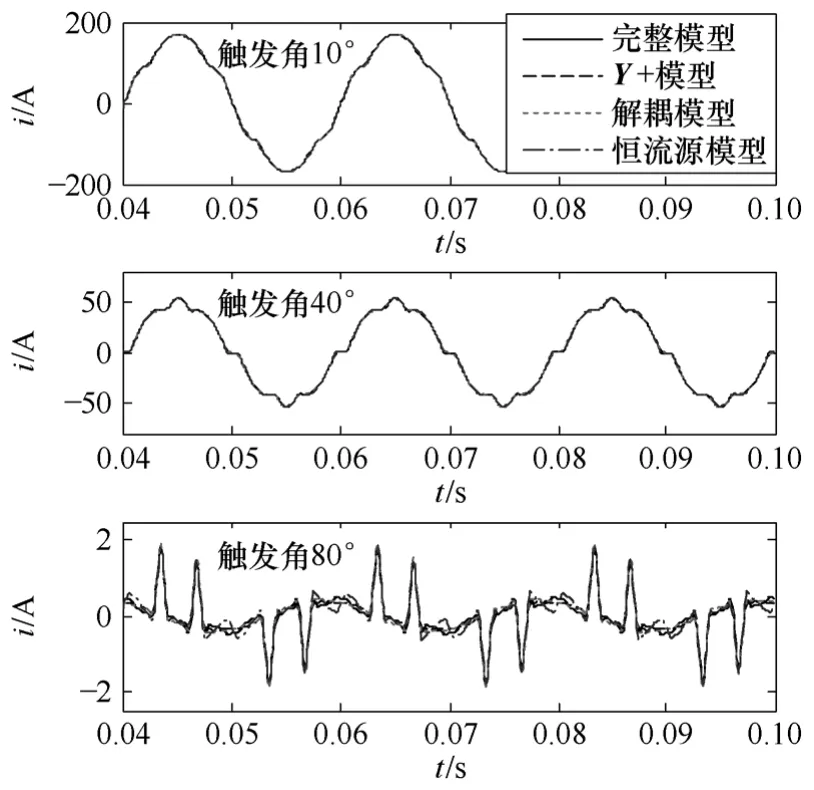
圖7 簡化模型結果對比Fig.7 Results comparison of the simplified models

可見觸發延遲角較小時，各簡化模型和完整模型吻合程度都較高，隨觸發延遲角的增大，簡化模型的精度降低。為精確衡量三種簡化模型的準確度，定義E為簡化模型和完整模型之間的誤差

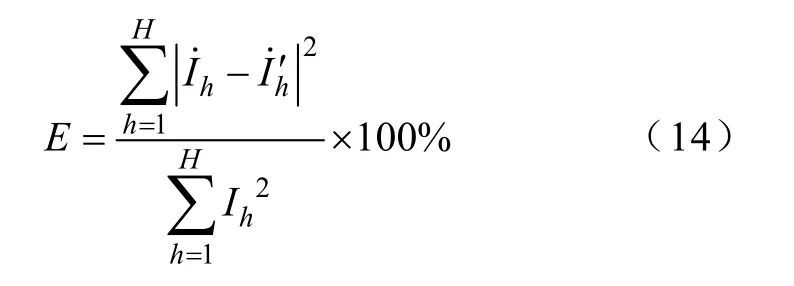
式中，為由完整模型得出的h次諧波電流值；為由各簡化模型得出的h次諧波電流值。

表2 給出了不同觸發延遲角時各簡化模型與完整模型之間的誤差E。當觸發延遲角α≤70°時，Y+模型、解耦模型以及恒流源模型的精度都較高；但當觸發延遲角α＞70°時，簡化模型的結果和完整模型的結果有差異，這是因為隨著觸發延遲角的增大，諧波電壓和諧波電流之間的耦合程度增強。然而，隨觸發延遲角增大，TCRs 產生的諧波電流實際值也將非常小。因此在工程應用中，若對模型精度要求不高，在較大觸發延遲角下仍可采用各簡化模型。簡化模型的意義在于，可減小諧波潮流計算中形成導納矩陣的工作量，加快計算速度。特別是當利用TCRs的解耦模型時，各次諧波頻率下的諧波潮流可解耦計算，計算量將大為減小。

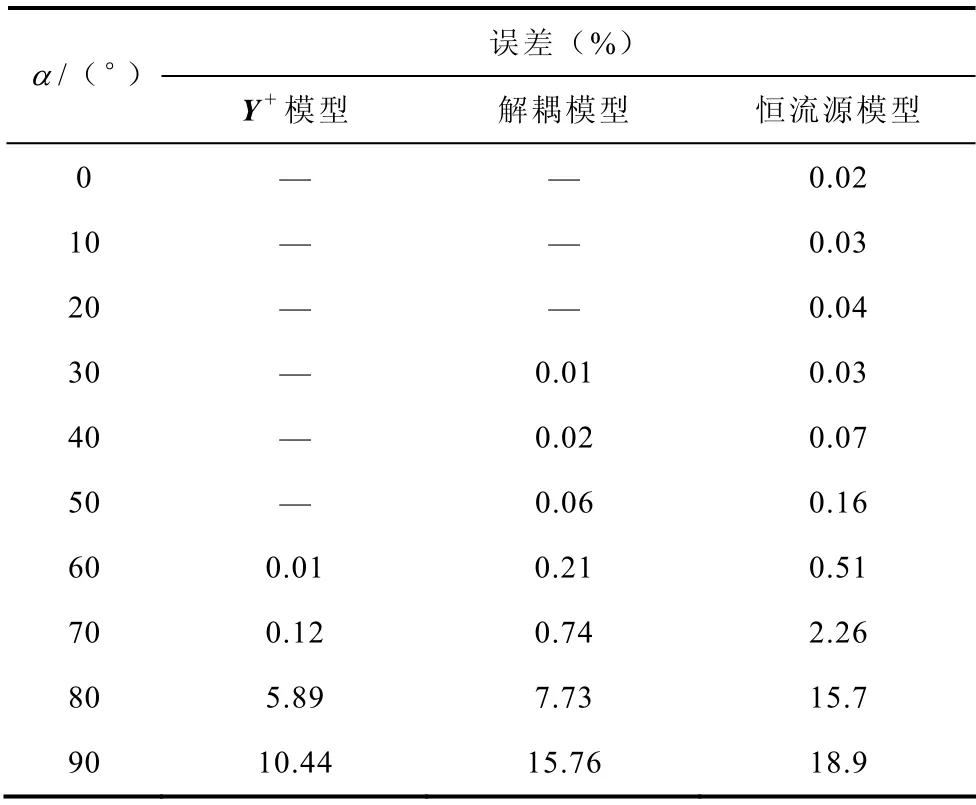
表2 簡化模型與完整模型的誤差Tab.2 Discrepancy evaluation for the simplified models

6 結論

本文基于TCRs的諧波耦合矩陣模型，對TCRs的諧波產生特性進行了分析。在TCRs的諧波產生過程中，基波電壓的影響最大、與諧波電流次數相同的諧波電壓的作用次之、其他諧波電壓及其共軛分量與諧波電流的互耦合影響最小。

通過對TCRs的諧波耦合矩陣模型的物理意義和各元素取值規律分析，得出TCRs 諾頓等效電路中諧波自導納以及經典恒流源模型的解析計算公式。研究了恒流源模型、解耦模型以及Y+模型，在不同觸發延遲角時的計算精度。當觸發延遲角α≤70°時，各模型精度較高；當觸發延遲角α＞70°時，各簡化模型都將引入不同程度的誤差。結論可為工程中TCRs 諧波模型的合理選擇提供理論指導。

[1]劉其輝,蔚芳,康長路.基于電網電壓定向矢量變換的SVC 平衡化補償策略[J].電工技術學報,2009,24(8):147-153.Liu Qihui,Wei Fang,Kang Changlu.Balancing compensation strategy of SVC based on grid-voltage-oriented vector transformation[J].Transactions of China Electrotechnical Society,2009,24(8):147-153.

[2]丁仁杰,劉健,張雋,等.一種基于瞬時無功功率理論的SVC 控制方法[J].電工技術學報,2006,21(5):47-51.Ding Renjie,Liu Jian,Zhang Jun,et al.New control method of SVC based on instantaneous reactive power theory[J].Transactions of China Electrote-chnical Society,2006,21(5):47-51.

[3]劉玉雷,解大,張延遲.靜止無功補償器用于抑制廠用電系統電壓波動仿真[J].電力系統自動化,2006,30(16):97-101.Liu Yulei,Xie Da,Zhang Yanchi.Simulation of static var compensator to restrain the voltage fluctuation of electric auxiliary system[J].Automation of Electric Power Systems,2006,30(16):97-101.

[4]張定華,桂衛華,王衛安,等.新型電氣化鐵道電能質量綜合補償系統的研究及工程應用[J].電工技術學報,2009,24(3):189-194.Zhang Dinghua,Gui Weihua,Wang Weian,et al.Study and application of a new power quality combined compensation system for electrified railway[J].Transactions of China Electrotechnical Society,2009,24(3):189-194.

[5]帥智康,羅安,劉定國,等.靜止無功補償器與有源電力濾波器聯合運行系統[J].中國電機工程學報,2009,29(3):56-64.Shuai Zhikang,Luo An,Liu Dingguo,et al.Combined system of static var compensator and active power filter[J].Proceedings of the CSEE,2009,29(3):56-64.

[6]Task Force on Harmonics Modeling and Simulation.Modeling and simulation of the propagation of harmonics in electric power networks,part I:concepts,models and simulation techniques[J].IEEE Transactions on Power Delivery,1996,11(1):452-465.

[7]Task Force on Harmonics Modeling and Simulation.Characteristics and modeling of harmonic sources-power electronic devices[J].IEEE Transactions on Power Delivery,2001,16(4):791-800.

[8]Chang G W,Lin Y.Modeling of nonlinear components for harmonic studies[C].2003 IEEE Power Engineering Society General Meeting,Toronto,Canada,2003:1188-1193.

[9]Montano J C,Gutierrez B J,Lopez O A,et al.Effects of voltage waveform distortion in TCR type compensators[J].IEEE Transactions on Industrial Electronics,1993,40(3):373-383.

[10]Xu W,Marti J R,Dommel H W.Harmonic analysis of systems with static compensators[J].IEEE Transactions on Power Delivery,1991,11(2):183-190.

[11]Rico J J,Acha E.The use of switching function and Walsh series to calculate waveform distortion in thyristor-controlled compensated power circuits[J].IEEE Transactions on Power Delivery,1998,13(4):1370-1377.

[12]Osauskas C M,Wood A R.A frequency domain model of a thyristor controlled reactors[C].Proceedings of the Harmonics and Quality of Power,Athens,Greece,1998:923-929.

[13]Sun Y,Zhang G,Xu W,et al.A harmonically coupled admittance matrix model for AC/DC converters[J].IEEE Transactions on Power Systems,2007,22(4):1574-1582.

[14]鄭偉杰,徐文遠.TCR 非線性特性的線性耦合導納矩陣模型[J].中國電機工程學報,2008,28(1):59-64.Zheng Weijie,Xu Wenyuan.Harmonically coupled linear matrix model for harmonic analysis of TCR[J].Proceedings of the CSEE,2008,28(1):59-64.

[15]Medina A,Garcia N.Fast time domain computation of the periodic steady state of systems with nonlinear and time-varying components[J].International Journal of Electrical Power & Energy Systems,2004,26(8):637-643.