用多面體逼近球體及其在工業設計中的應用

黃 穗， 韓春明

（1. 中國電子科技集團公司第三十八研究所，安徽 合肥 230088；2. 合肥工業大學建筑與藝術學院，安徽 合肥 230009）

多面體具有豐富的幾何表現力，在人類的生產生活中具有廣泛的應用，如圖1所示。因此，關于多面體的各種研究也在廣泛開展，探討多面體的構成[1-2]，以及其在裝潢[3]，機械加工[4]，包裝[5-6]，服裝[7-8]，三維人體建模[9]，建筑[10]，地質[11]，化學[12]等方面的應用。

無論是在建筑設計、產品設計、雕塑創作還是其他藝術設計中，球體是經常被運用的設計元素。但由于受到材質、工藝、技術、成本、視覺效果等諸多因素影響，現實中的球體造型往往用多面體來代替，如圖2所示。圖3是計算機輔助設計中常用的兩種用來表示球面的網格，其實也是多面體對球體的逼近。

目前，對多面體表示球體的方法已有大量討論和研究，比如采用切割、變形等多種幾何方法使多面體逐漸達到近似球體的效果[13]。在此基礎上，本文提出了用多面體逼近球體的評判準則，以及在這些準則下改進逼近效果的方法。最后以實例說明多面體逼近球體在工業設計中的應用。

圖1 多面體造型示例

圖2 用多面體構建的球形建筑和產品

1 多面體逼近球體的評判準則

用多面體逼近球體，即是用多邊型構成的封閉表面去近似地表示球面。球面是距空間一定點為等長的所有點構成的光滑的凸起封閉曲面，此曲面上任何一點與其它點的地位都是平等的，因此很自然地對逼近它的多面體有如下規則：

1）每個頂點處的多面角的各平面角之和小于360°，但越接近于360°越好；

2）每條棱處的二面角小于180°，但越接近于180°越好；

3）有外接球面，即各頂點共球面；

4）有內切球面，即各個面與同一球面相切；

5）各頂點在空間分布得盡量均勻，因此各面盡可能為正多邊形，且各面的面積差別越小越好；

6）多面體表面各點到被逼近球體的球心的距離越接近越好，即表面上點離中心最遠的距離與最近的距離之比（姑且稱之為遠近比）越接近于1越好。如外接球面和內切球面都存在，則它們的半徑越接近越好，且要求盡量共心；

7）頂點、面和棱盡量少，以降低建造成本，增加結構強度。

以上規則反映了球面的特性，例如規則1），既體現了球面的彎曲性質，又對其光滑性作了要求。若各平面角之和等于360°，則組成此多面角的各面或其中部分面共面，于是此多面角的各棱或部分棱就成為多余。而各平面角之和越接近于360°，則多面體的表面就越光滑。規則 2）也是如此。

上述規則未必都能滿足，但滿足得越多越好。例如，在現實中有些逼近球體效果很好的多面體，其外接球面和內切球面未必同時存在，圖3中的兩種網格就是，后面還會用其它實例說明。而且各規則未必都能被同時兼顧，例如規則7）和前幾條，應根據具體情況綜合權衡。

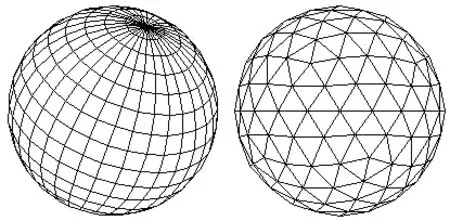
圖3 計算機輔助設計球面的兩種常用表示方法

2 改進逼近效果的方法

對已有的近似于球體的多面體，一般常用以下兩種方法對其逼近效果加以改進：

1）削去頂點，形成一新的多邊形面，其邊數等于原頂點處多面角的面數，如圖4所示，削去頂點A后，形成新的四邊形面BCDE。

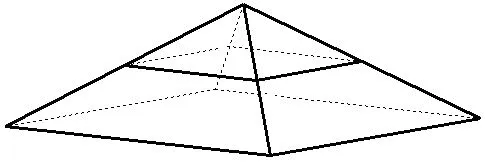
圖4 削去多面體的頂點

用初等幾何的方法即可證明，在新多邊形各頂點處的多面角，其各平面角之和都大于被削頂點處各平面角之和。這是對規則1）的逼近效果的改進。

多面體表面到被逼近球體的球心距離最遠的點在頂點處，因此削去頂點后，多面體表面各點到球心的距離更加接近。這是對規則6）的逼近效果的改進。

2）多面體表面各多邊形向其中心收縮，則產生削去原多面體頂點和棱的效果，在原頂點處產生新的多邊形面，邊數與該頂點處多面角的面數相同，在原棱處產生新的四邊形面。

圖5中，頂點A周圍各面收縮后，頂點A被削去，產生了一個新的四邊形（多面角A為四面角），棱AB被削去，產生一個新的四邊形。

圖5 多面體表面收縮，頂點被削去，產生新的多邊形，被削去的棱處出現新的四邊形

易證多面角被削去后，在所產生的多邊形各頂點處的多面角，其周圍平面角之和都大于被削多面角周圍平面角之和。而且，收縮后的面的各邊處的二面角大于相應被削去的棱處的二面角。如圖5右圖中，頂點C處周圍各平面角之和大于中圖中頂點A處周圍各平面角之和；右圖中棱CD處的二面角也大于中圖中棱AB處的二面角。

這樣一來，規則 1），2），6）的逼近效果都得到了改進。

3 正多面體對球體的逼近效果及改進

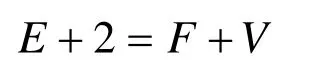
正多面體是由同種正多邊形為面構成的多面體，其各頂點和各面分布得最均勻，且具有同心的外接球面和內切球面。由于多面體的棱數E，面數F和頂點數V必須滿足歐拉公式故正多面體只有5種（也稱柏拉圖立體[13]），即正四面體，正六面體，正八面體，正十二面體和正二十面體（圖6）。顯然正多面體中，正十二面體和正二十面體對球體的逼近效果較好。表1對這兩種正多面體的逼近效果作了比較。

對正多面體可進一步改進使它們更好地逼近球體。一般可采用如下兩種方法。

方法1削去頂點，在每個頂點處截去一個正多棱錐，則原頂點處產生一個新的正多邊形面，而原頂點被每條棱上新產生的兩個頂點代替。若ViVj為原來的任一條棱，現被截成Vi'Vj'，其中0＜α＜ 1 /2。表面上原來的正n邊形變為2n邊形。

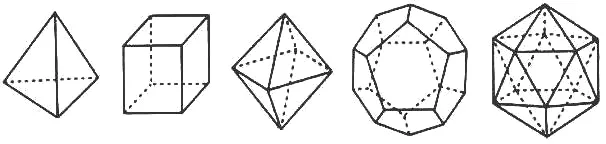
圖6 5種正多面體

表1 正十二面體與正二十面體逼近球體的效果比較

方法2 表面收縮。若原表面為正n邊形， 其頂點為則收縮后的多邊形頂點為 {Pk'},k= 1 ,… ,n，其中原頂點和棱都被削去，其原位置分別產生新的正多邊形和矩形。

下面以正二十面體為例，采用上述兩種方法進行改進。

使用方法1，在頂點處削去一個正五棱錐，形成一個正五邊形面。選取α=1/3，使原來的棱保留中間的三分之一，三角形面被截成一個正六邊形（圖7）。這樣得到的多面體表面由12個正五邊形和 20個正六邊形組成，這是一個半正多面體（由幾種邊長相同的正多邊形圍成的立體，也稱阿基米得立體），表面有60個頂點，每個頂點為兩個六邊形和一個五邊形形成的三面角的頂點，3個平面角之和為348°。兩個相鄰六邊形構成的二面角即原正二十面體相鄰面構成的二面角，其大小約為 138.19°（余弦值為而相鄰的五邊形和六邊形構成的二面角約為 1六邊形面由原三角形切去3個角形成，故仍與原內切球面相切。顯然各頂點到原正 20面體的中心的距離相同，因此有外接球面，易算得外接球面與原內切球面的半徑比（也是遠近比）為。與12個正五邊形相切的球面半徑與原內切球面的半徑比為這就是說，改進后的多面體表面的12個正五邊形和20個正六邊形分別與兩個同心的球面相切，這兩個球面半徑略有不同（相差約1.02653倍），因此此多面體無內切球面。為使多面體的兩種正多邊形與相同的球面相切，可適當增加被截五棱錐的高度，使截得的正五邊形中心到多面體中心的距離等于原內切球面的半徑，但六邊形不再是正六邊形，六邊形與五邊形的公共邊略大于六邊形之間的公共邊。

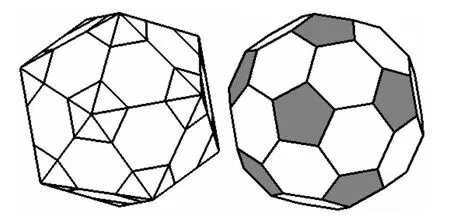
圖7 正二十面體削去頂點

使用方法2，收縮表面三角形，削去原多面體的頂點和棱，在原頂點處出現正五邊形，而在原有的棱處出現矩形。當時，三角形的邊長收縮為原邊長的≈ 0 .35倍時，兩三角形之間的矩形為正方形，這樣原來的正20面體成為由邊長相同的正三角形，正方形和正五邊形圍成的半正多面體，如圖8(a)所示。此多面體有 60個頂點，各頂點到多面體的中心的距離相同，即在以多面體中心為球心的外接球面上。多面體的表面由 20個正三角形，30個正方形和12個正五邊形構成。每個頂點處為四面角，分別為一個正三角形的內角，兩個正方形的內角和一個正五邊形的內角，它們的和為348°。三角形與正方形之間的二面角約為159.1°（其余弦為正方形與正五邊形之間的二面角約為 148.3°（其余弦為

此多面體的中心到其表面各正多邊形的最近點都是各正多邊形的中心，而三角形中心到多面體中心的距離即為原二十面體的內切球面半徑r。若記正五邊形和正方形的中心到多面體中心的距離分別為r5和r4，外接球面半徑為R，有R:r:r4:r5= 1 .0352:1:0.982:0.957，且其中最大與最小者之比（遠近比）R:r5= 1 .081555672。

由此可見，表面收縮法改進正二十面體逼近球體的效果比頂點削去法好。其實表面收縮法的遠近比還可減小。取時，三角形的邊長收縮為原邊長的 1 -3α≈ 0 .4428倍，這時正五邊形與正三角形的外接圓半徑相等，因此正五邊形與正三角形的中心到正多面體的中心距離相等，五邊形的邊長小于三角形的邊長，四邊形不再是正方形，但各多面角和二面角不變，如圖8(b)所示。四邊形（矩形）的外接圓半徑（即對角線之一半）小于五邊形和三角形的外接圓半徑。因此，矩形中心到多面體中心的距離大于五邊形或三角形中心到多面體中心的距離，其比值約為 1.00052。所以這時的遠近比即為多面體各頂點到多面體中心的距離與三角形（或五邊形）中心到多面體中心的距離之比，約為1.05566。

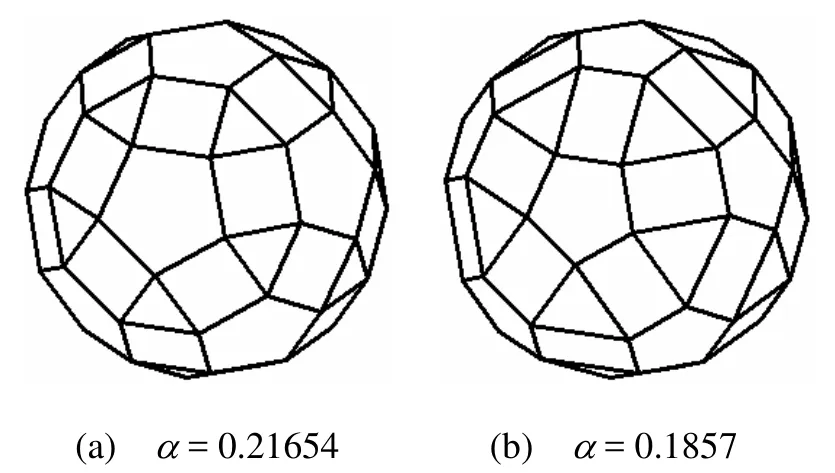
圖8 20面體經過面收縮后得到的多面體

從遠近比來看，取α= 0.1857的效果比α=0.21654的效果好，但視覺效果并不好，這是因為正方形變成矩形后，正五邊形周圍5個正三角形和矩形圍成的十邊形不再是正十邊形，如圖8所示，而且右邊的多面體中，以正五邊形為頂的臺體似乎更尖更凸。

4 多面體對球體的逼近在工業設計中的應用

相比于其他立體幾何形態，球體表面光滑，形態勻稱，能帶給人柔和感和親切感。因此在工業設計尤其是產品造型設計中得到大量應用。但是，由于審美的需要，光滑球體經常用多面體來近似表達，以突出豐富的視覺效果和層次感。圖9所示為一款項鏈的水晶吊墜設計，其看似球體的造型實際上是由切割后的多面體構成。在這里，用多面體近似表示球體可以增強水晶的折射度，充分展現水晶的光彩，同時球體的表達效果也沒有被削弱。而如果直接采用光滑的球面作為造型，則無法突顯其質地的華麗璀璨。

圖9 用多面體近似表達球體的水晶吊墜

除審美需求外，材料或工藝的限制也會使設計師考慮用多面體來代替球體達到效果，例如用鋼梁構建球形框架，用平板材料構造球型容器，用小塊皮革拼縫球類的外殼等，例如圖2。以足球為例，多數足球的外殼是用 20個正六邊形和12個正五邊形的皮塊拼成的，這正是圖7所示的削去正二十面體的頂點而得到的半正多面體，打足氣后，多面體外殼被撐成球體。盡管圖8所示的由二十面體表面收縮所得的多面體對球體有更好的逼近效果，但所呈現的視覺印象過于“零碎”，表面面數太多，反而會增加成本和加工復雜性，同時還可能降低結構強度。綜合考慮制造工藝、成本、結構強度、美觀效果等因素，對足球而言，圖7的方案應該更加可行。但在其它場合，例如球型建筑，大型球型容器，文獻[13]提出的包括圖8的各種方案也不失為很好的選擇。當然，根據本文所提出的逼近原則和實際對象的具體特性要求，還可設計出更加豐富多彩的產品外觀造型。

5 結 論

本文討論了用多面體逼近球體效果的評判標準和改進方法，并以實例說明這些方法在工業設計中的應用。從文中的實例可見，各標準之間往往不能同時兼顧，需要根據實際情況加以權衡。在實際應用中，應根據各種需要的輕重緩急分別盡可能地給予滿足。

[1] 劉金義,張 燕. 統一于三角面片的可靠多面體布爾集合運算[J]. 工程圖學學報,2002,(1): 53-62.

[2] 周年國. 形態的數字化生成及其特點淺析[J]. 藝術與設計(理論),2007,(11): 106-108.

[3] 周冬梅. 從立體構成角度解讀霓虹燈設計[J]. 科技信息,2009,(11): 501-502.

[4] 葛研軍,等. 基于光線跟蹤的虛擬數控車削加工圖形生成技術[J]. 中國圖象圖形學報,1999,(1):28-32.

[5] 王 薇. 立體構成與包裝設計[J]. 包裝世界,2000,(4): 27.

[6] 張麗紅. 包裝的造型設計[J]. 上海包裝,2001,(4):21-22.

[7] 朱李麗,等. 三維服裝 CAD中人體建模綜述[J]. 武漢科技學院學報,2004,(2): 19-21.

[8] 谷 林,張 欣. 服裝CAD中三維人體建模方法綜述[J]. 針織工業,2006,(5): 36-38.

[9] 胡 敏,等. 基于特征的三維人體建模[J]. 天津工業大學學報,2002,(5): 80-82.

[10] 王 暉,曹 康. 鑲嵌幾何在當代建筑表皮設計中的應用[J]. 浙江大學學報(工學版),2009,(6):1095-1101.

[11] 劉金義,程小茁. 一種多層地層實體造型方案及其實現[J]. 工程圖學學報,2002,(3): 51-58.

[12] 宓錦校,等. 動態三維真彩色晶體結構繪畫系統的設計[J]. 計算機與應用化學,2000,(4): 367-370.

[13] 彭君智. 3D立體變變變[J]. 數學傳播,2001,(3):68-80.