獨立時差計算公式的錯誤分析＊

劉慎熊 周 黎 張長清

（武漢交通職業學院，湖北 武漢 430065）

1 問題的提出

在現行各版本施工組織學教材中，求單代號網絡計劃的獨立時差的計算公式皆為：

可是，在教學和實踐的過程中，發現在某些工程中應用這個公式計算單代號網絡計劃的獨立時差時，其結果與同一工程的雙代號網絡計劃是不同的。不是數值不對，就是出現了不可思義的負數。（這個不可思義，是指這個負數的絕對值甚至大于前后工作的總時差之和）。我們知道一個工程既可以表達為單代號網絡計劃，也可以表達為雙代號網絡計劃。而且，同一項工作的所有時間參數在這兩種計劃中應該是一致的。但在使用公式（1）時獨立時差卻出現有時不一樣的問題，這是什么原因呢？

雙代號網絡計劃獨立時差的計算公式是：

公式（2）定義的雙代號網絡計劃的獨立時差的概念及推導是清楚的、正確的，因此公式（2）是不會有問題的。而對公式（1）的max｛IFh｝，總感覺含義似是而非，且無法作出概念上的清析解釋，這樣看來，問題或許就出在公式（1）上。為了找到答案，必須對公式（1）作深入的研究和探討。

2 獨立時差的含義及公式分析

獨立時差是指在既不影響緊前工作的最遲完成，又不影響緊后工作的最早開始的前題下，本工作的機動時間。考慮到自由時差對緊后工作沒有影響，獨立時差也可以表達為是自由時差中對緊前工作最遲完成不產生影響的那一部分機動時間。也就是說，獨立時差是在本工作的自由時差中減掉其對緊前工作最遲完成產生影響的那部分后，所得的差。公式（1）和公式（2）似乎都有點這個意思。

在雙代號網絡計劃圖中，本工作的緊前工作中既有實工作也有虛工作，它們的最遲完成時間是一樣的，都是LFh－i，因此本工作自由時差對所有緊前工作的最遲完成產生的影響都是一樣的，即都等于LFh－i－ESi－j＝IFh－i，從自由時差中減去這個影響值，剩下的差就是本工作的獨立時差，可見公式（2）是正確的。

但是在單代號網絡計劃圖中，由于沒有中間虛工作，所以在把一項工程的雙代號網絡圖轉換成單代號網絡圖時，就可能會出現某一工作跨越虛工作直接成為本工作的緊前工作。（為了方便，我們把它稱為名義緊前工作）。如圖1所示：（a）是某雙代號網絡圖的一部分，（b）是該圖轉換成單代號網絡圖后與（a）相應的部分。

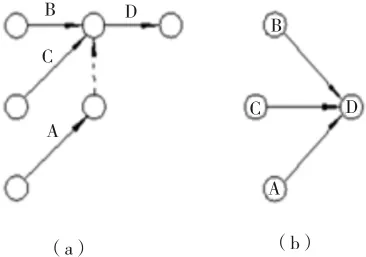
圖 1

A工作就是D工作的名義緊前工作，它的最遲必須完成時間值，必然小于或等于其余兩緊前工作B和C的最遲完成時間值。那么D工作的自由時差對A工作最遲完成的影響必然小于或等于對B、C兩工作最遲完成的影響。故我們要取這個影響的最大值，完全可以不考慮對A工作最遲完成的影響。但是公式（1）卻把這個最大值定義為緊前工作相關時差的最大值：max｛IFh｝。這里就沒有排除A工作的意思，因為不能保證A工作的相關時差一定比B和C兩個工作的相關時差小，相反A工作的相關時差有時確實是最大值。（在后面實例圖3上，可以看到這種情況。如：D工作的名義緊前工作A的相關時差是4，而工作B的相關差是0）。也就是說公式（1）考慮了不該考慮的選項，而應該考慮的選項又沒有考慮，或者說選擇最大值的標準不對。就像是本要選一個統軍將才，結果選了一位百發百中的神槍手。這里正確選項應該是“本工作自由時差對所有緊前工作最遲完成產生影響的最大值”，而不是公式（1）中定義的“所有緊前工作相關時差的最大值”，這也許就是問題的根源所在。下面我們用一個實例來應證公式（1）是不正確的。

3 實例論證

圖2是某工程雙代號網絡計劃圖，經過計算，各時間參數都按標注圖例填入相應的位置。而圖3是這同一個工程的單代號網絡計劃圖，各時間參數也填入相應的位置。其中單代號網絡計劃圖的獨立時差是使用公式（1）計算出來的。

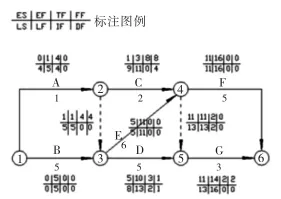
圖 2

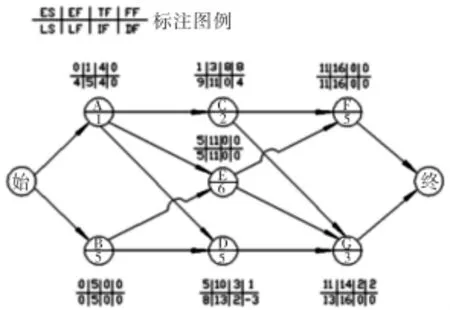
圖 3

這兩種網絡計劃中的同一工作各參數應該是完全一致，但是可以發現圖3中D工作的獨立時差與圖2中D工作的獨立時差不同。下面是使用公式（2）、公式（1）及定義式計算的過程和結果。

圖2是雙代號網絡計劃，獨立時差用公式（2）計算：

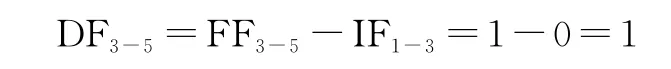
或者用定義式：

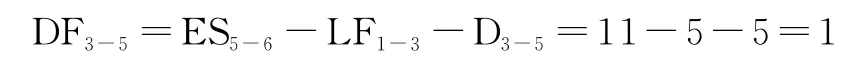
圖3是單代號網絡計劃，獨立時差用公式（1）計算，圖2中的工作3－5在圖3中就是工作D。它有兩個緊前工作A和B。用公式（1）DFi＝FFi－max｛IFh｝來計算，則有：

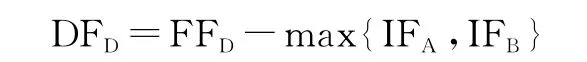
而從圖3中可以看到FFD＝1，IFA＝4，IFB＝0。于是有DFD＝1－max｛4，0｝＝1－4＝－3

在這三個答案中，用公式（2）計算的結果是毋庸置疑的，因為，它與使用獨立時差的定義式所得到的結果完全一致，那只能說明使用公式（1）所得到的結果是錯誤的。

4 正確公式的推導

4．1 公式推導

單代號網絡計劃中獨立時差應該根據獨立時差的定義及單代號網絡圖的特點進行推導。

根據獨立時差的定義，又考慮到在單代號網絡圖中因沒有中間虛工作，i工作的所有緊后工作的最早開始時間不盡相同，故要取最小值；同樣i工作的所有緊前工作的最遲完成時間也不盡相同，故要取最大值。即：

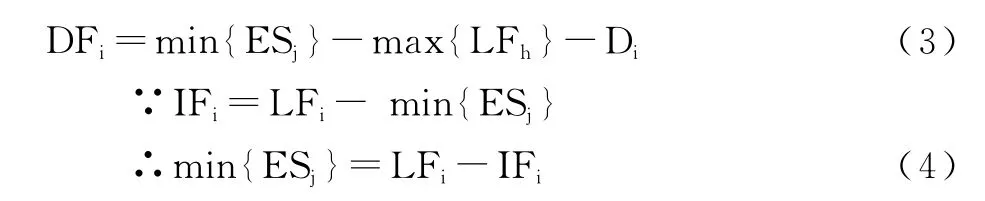
（4）代入（3）得：

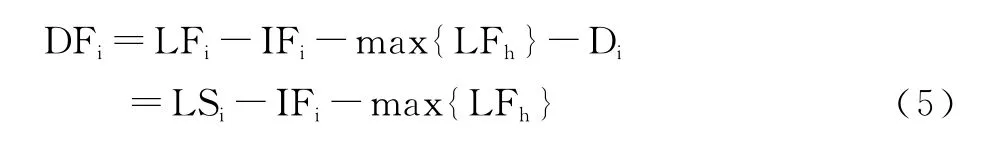
又∵TFi＝LSi－ESi

（6）代入（5）得：

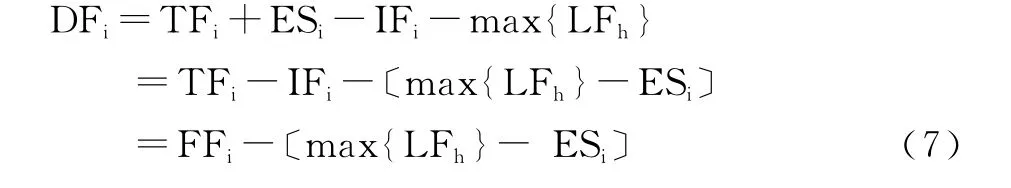
這個（7）式就是我們給出的正確公式。這個公式中max｛LFh｝表示本工作所有緊前工作的最遲完成時間的最大值，這也可認為是排出了那些名義緊前工作。而方括號里面的內容所表達的正是我們前面所說的選項：“本工作自由時差對所有緊前工作最遲完成產生影響的最大值”。這與我們前面分析的結論是吻合的。

4．2 驗證

現在我們對圖3中D工作的獨立時差用（7）式進行計算：

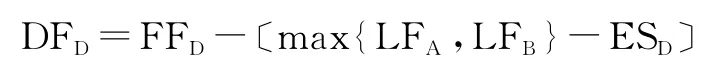
從圖2，3中我們知道FFD＝1，LFA＝5，LFB＝5，ESD＝5

即：DFD＝1－〔max｛5，5｝－5〕＝1

可見經過檢驗，這個式子的正確性是顯而易見的。把它用于上面的計算，得出的結果與雙代號網絡計劃的結果是一致的。

5 結論

（1）在計算單代號網絡計劃獨立時差時，應該用（7）式來計算。即：

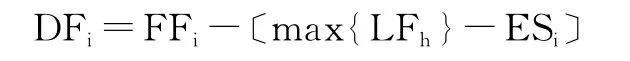
（2）獨立時差出現負數時的含義及計算時應注意的問題。負數表明本工作對緊前工作的最遲完成或者對緊后工作的最早開始產生了影響，或者對緊前緊后工作都產生了影響。這個負數的絕對值就是這個影響程度，但是這個絕對值，不能大于前后工作的總時差之和。因為如果這個絕對值大于前后工作的總時差之和，就意味著本工作的最早開始時間在緊前工作的最早完成時間之前，同時本工作的最遲結束時間在緊后工作最遲開始時間之后。而這是絕對不可能發生的現象，除非算錯了，正如本例一樣。所以我們認為，如果獨立時差算出負數，可以直接填入，沒有必要令其等于零。

（3）關于“名義緊前工作”的處理方法，在特殊情況下，即若所有緊前工作都是名義緊前工作時，不能全部排除，必須在這些“名義緊前工作”中取最遲完成時間的最大值。即便是這樣，也并不影響公式（7）的正確性。