柔性身管的RBF神經網絡PID控制
田福慶,李克玉,李進衛
(1.海軍工程大學 兵器工程系,湖北 武漢 430033;2.中國船舶重工集團公司第七一三研究所,河南 鄭州 450015)
柔性身管的RBF神經網絡PID控制
田福慶1,李克玉1,李進衛2
(1.海軍工程大學 兵器工程系,湖北 武漢 430033;2.中國船舶重工集團公司第七一三研究所,河南 鄭州 450015)
由于艦炮身管的彎曲振動,傳統的利用炮管軸角位移進行反饋控制的方法無法精確控制炮口指向。針對這一缺點,提出了一種利用炮口角位移作為隨動系統位置環反饋信息的控制結構。為模擬身管的振動,應用多剛體動力學對艦炮身管進行了柔性體建模。為改進后的控制結構設計了基于RBF神經網絡整定PID參數的控制器,并與傳統PID控制器的控制效果進行了仿真對比,驗證其對于提高隨動系統控制精度的有效性。
柔性身管;隨動系統;RBF神經網絡;SimMechancis
0 引言
現代小口徑艦炮身管具有較大的長徑比,因自重而產生一定的靜彎曲[1],并且在發射時,一般處于高速跟蹤狀態,轉動慣量及負載力矩變化大等非線性因素,常使身管產生彎曲振動。通過對炮口振動與彈著點坐標的相關性分析,發現炮彈出口時的炮口位移與彈著點坐標存在著較好的相關性,振動直接影響散布[2]。無論艦炮系統的振動有多復雜,其作用最終在炮口有所反映。因此,對炮口振動的研究和對炮口指向的控制就顯得較為重要。
文獻[3]系統闡述了雙電機驅動的火炮隨動系統的組成,建立了該系統的模型,但沒有考慮身管振動對控制精度的影響。文獻[4]為艦炮設計了以身管角位移作為隨動系統的反饋量的火炮隨動系統,試圖直接對身管指向進行控制,但沒有考慮身管振動對隨動系統中的機電耦合產生的影響。另外在國外,也有將可編程脈沖信號發生器所產生的阻尼信號傳遞給火炮隨動系統,以抵消火炮振動,減小火炮射彈散布的報道[5],即通過對隨動系統進行反饋控制,用隨動系統來補償炮口的振動。從結果上看,有一定的效果。
針對身管振動對射擊精度影響較大及其非線性的特點,本文提出一種利用炮口角位移作為隨動系統位置環反饋信息的控制結構,仿真驗證其提高控制精度的有效性。
1 模型建立
艦炮的隨動系統中聯系了諸多的傳動裝置和變速裝置,同時炮耳軸和身管也影響著艦炮隨動系統的控制性能。艦炮機構簡圖如圖1所示。
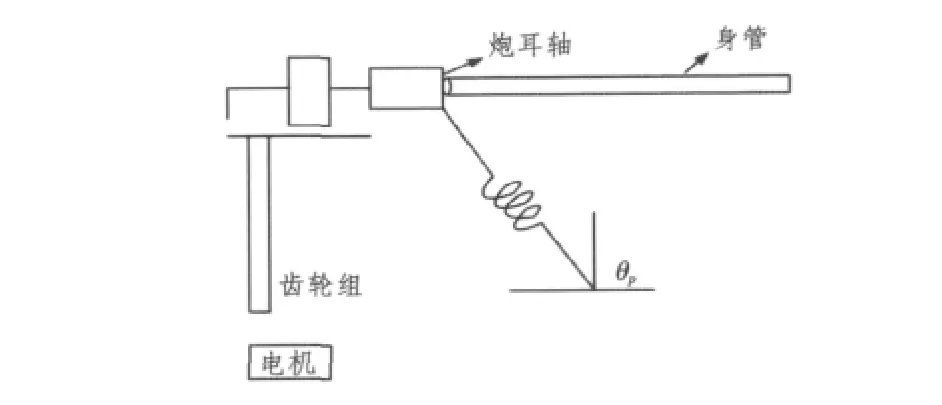
圖1 艦炮隨動系統機構簡圖Fig.1 Structure diagram of servo system
1.1 建模理論
由于艦炮身管的彎曲振動控制要用計算機控制系統來實現,因此應盡量使所建立的運動方程簡單和易于離散化,故選擇以多體系統建立動力學方程的方法。
這里以某艦炮為例,其身管的構型,包括各段長度li,橫截面積Ai,對質心的轉動慣量Ii,材料的彈性模量E,以及密度ρ等幾何物理特性均可以得到。將艦炮身管依照截面尺寸劃分為5個單元體,各單元體間的連接簡化為彎曲彈簧、彎曲阻尼和光滑鉸鏈(消除沿身管方向的位移),其力學模型如圖2所示。
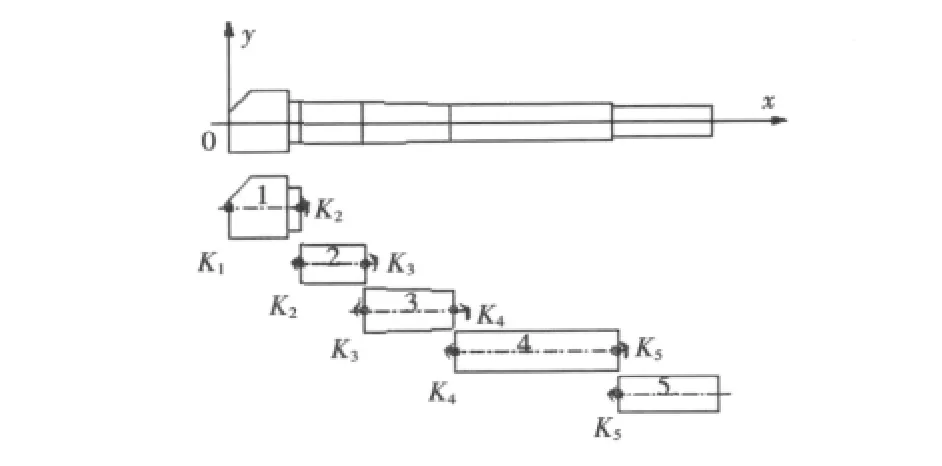
圖2 炮管多體系統力學模型Fig.2 Dynamic model of multi-body system of gun tube
若將炮管視為彈性體,考慮炮管的彎曲振動對炮口位移的影響,則火炮是一個無限自由度系統。從振動理論可知,系統的振動響應特性主要是由其低階模態決定的,因此可以用炮管的低階模型來近似,其數學模型的簡化形式為:
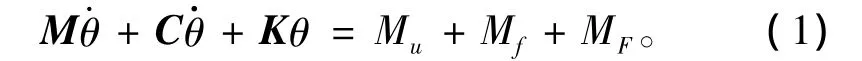
式中:M,C和K分別為火炮的廣義質量、阻尼和剛度矩陣;Mu,Mf和MF分別為控制力矩和炮管搖擺作用下的自身慣性力矩和射擊載荷引起的作用力矩。
對火炮身管建立可變形體動力學方程,設各單元轉角
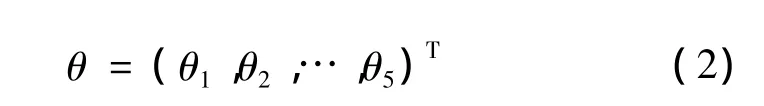
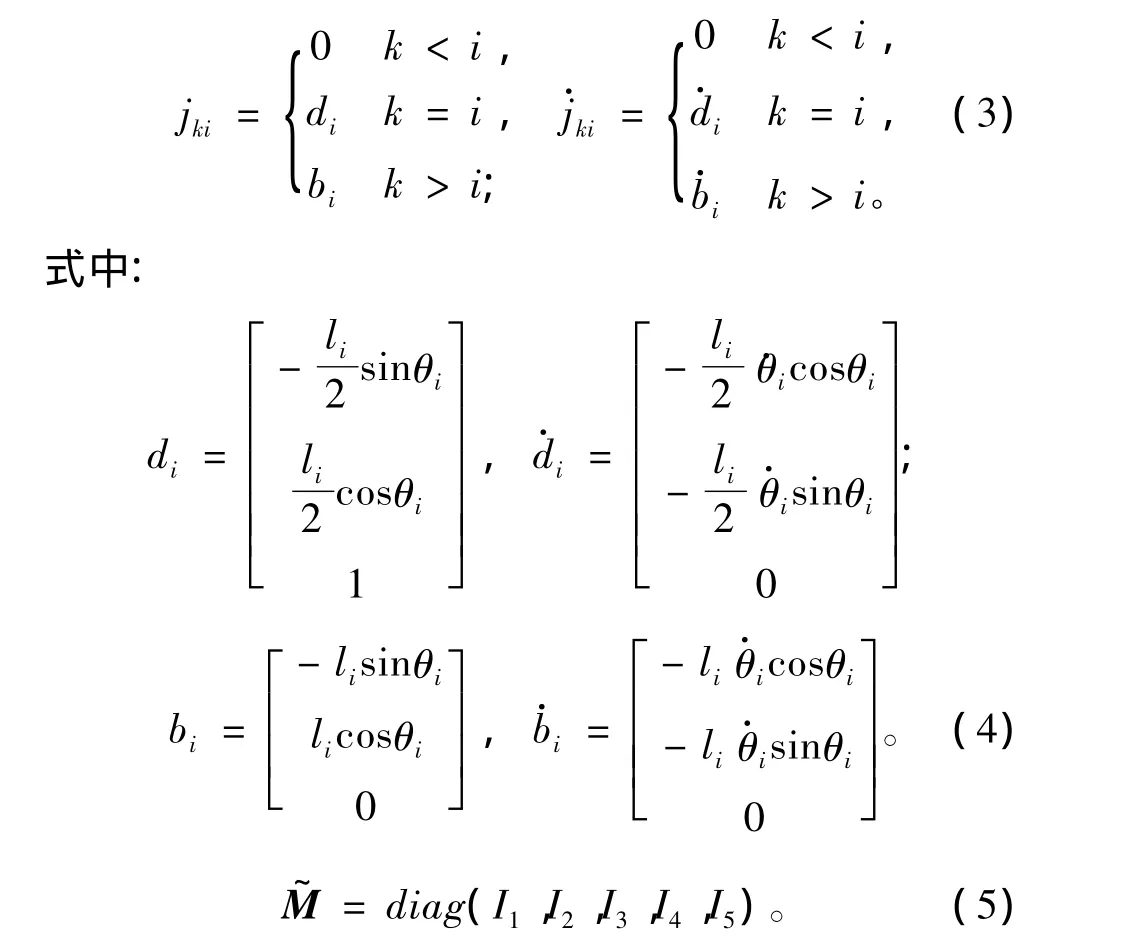
系統質量矩陣為:

系統剛度矩陣為:
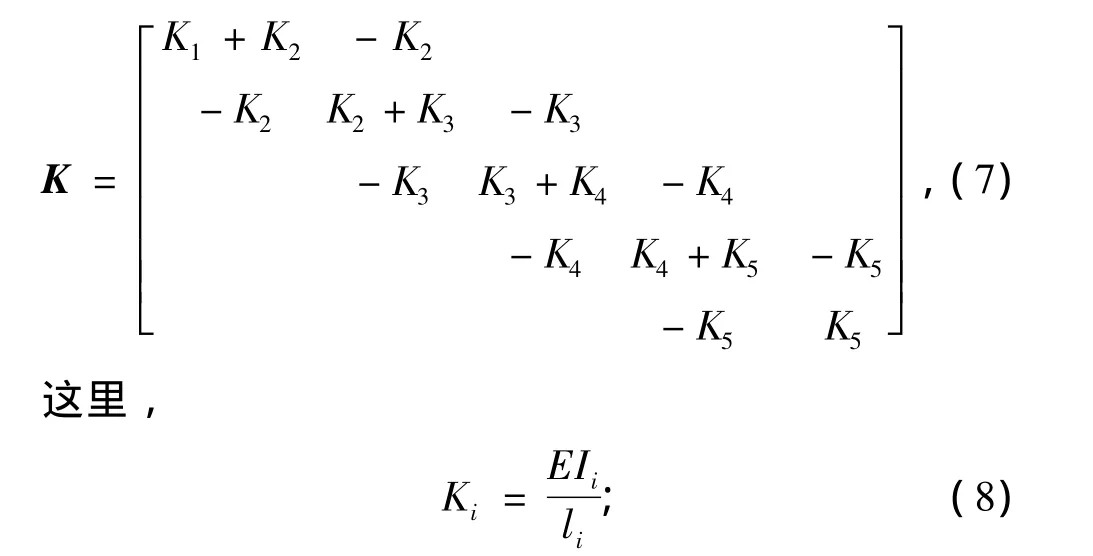
系統阻尼矩陣為:

在小角度時,矩陣C由結構阻尼確定,簡化為比例阻尼形式。對多自由度模型,在小角度時,令sinθi≈0,cosθi≈1,仿真模型中,各參數在Matlab工作空間中生成向量文件。
1.2 身管模型的SimMechanics實現
SimMechancis中的Flexible Element模塊提供了多體系統單元體的建立方法。將5個身管單元體的密度,彈性模量等具體參數在Matlab工作空間中生成向量文件,在Simulink文件中選擇Flexible Element模塊,然后執行Mask Subsystem命令,就可以將身管的密度,彈性模量等數據生成的向量文件導入其中,以生成身管單元體的SimMechancis模型。為方便起見,5個身管單元體的參數設置均相同。參照以多體系統方法建立的動力學方程,選取5個Flexible Element模塊封裝于1個Subsystem模塊中,以模擬身管的多體系統建模,并命名為Gun Tube,如圖3所示。
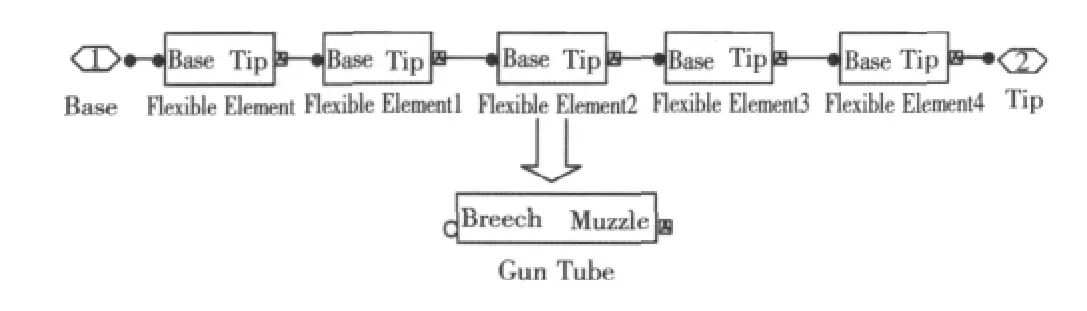
圖3 柔性身管模型Fig.3 Model of flexible tube
加入驅動和測量模塊,得到柔性身管的 Sim-Mechancis仿真模型,如圖4所示。其中,輸入信號為身管剛性連接的高低齒弧輸出的角速度,即身管軸線的角速度,經過積分可得到角位移量,微分可得到角加速度,Joint Actuator采集的就是這3個運動信息,然后驅動身管運動。Flexible Element Actuator采集的是柔性振動后炮口的角速度信息。其中,Out1,Out2和Out3分別為炮口繞X軸、Y軸和Z軸的角速度,繞Z軸的炮口速度為身管俯仰方向的角速度,因為本文研究的是高低隨動系統,所以只需輸出繞Z軸的炮口速度。為便于表示,以大齒輪角速度為輸入,以Out3為輸出,將該模型封裝,命名為模塊FT。
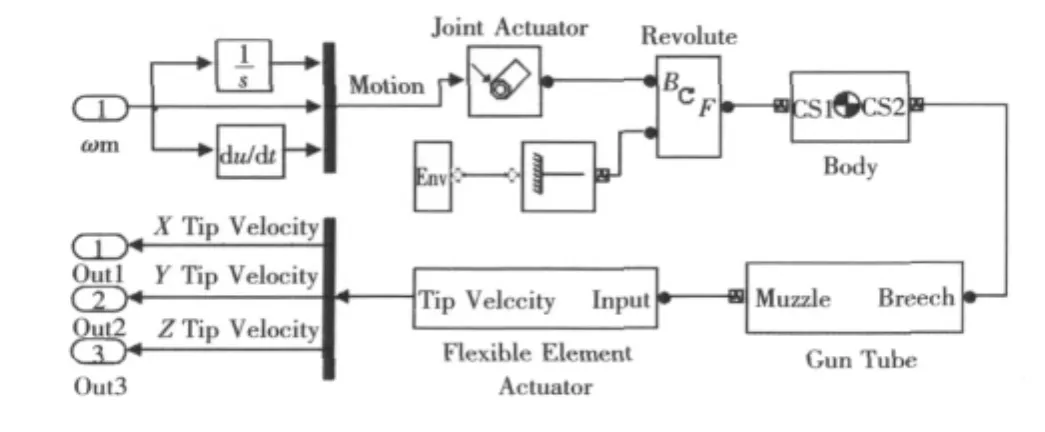
圖4 柔性身管的仿真模型Fig.4 Simulation model of flexible tub
2 控制結構改進
傳統的隨動系統只是控制炮管軸的方向,身管振動相當于開環控制,所以無法對炮口的最終指向進行有效控制。因此,本文從炮口部獲取角位移信息作為隨動系統位置環的反饋信息,核心思想是利用炮口信息對系統進行反饋,則把身管振動包括在閉環控制中,以保證炮口指向為理論瞄準方向,圖5為其系統結構圖。

圖5 控制炮管指向的系統結構圖Fig.5 Structural diagram of the system controlling directionality of muzzle
將該柔性身管模型搭建在文獻[3]建立的雙電機驅動的隨動系統上,且采集炮口的角位移作為位置環的反饋信息,就得到了如圖6所示的艦炮隨動系統模型。圖中,WACR1,WACR2,WASR,WAPR,WATR分別為電流調節器1、電流調節器2、速度控制器、位置控制器和雙電機聯動控制器。其中,位置環的控制算法是系統的控制核心。
3 RBF網絡PID控制器的設計
傳統的PID控制方法是在獲取對象數學模型的基礎上,根據某一整定原則來確定PID參數。然而,身管振動具有高度非線性及時變性等特點[6],若艦炮隨動系統將炮口指向的控制包含閉環控制之內,則很難得到系統的精確數學模型,傳統的PID控制效果并不理想。因此,應考慮在PID控制中,PID參數的整定應不依賴于對象的數學模型,而且PID參數能在線調整,以滿足實時控制的要求。
神經網絡具有很強的容錯性和自學習、自組織、自適應能力,以及非線性映射能力和獨特的聯想、記憶、儲存能力。從理論上講,RBF網絡和BP網絡一樣可以近似任何的連續非線性函數。RBF網絡在局部逼近中,對于每個輸入、輸出數據對,只有少量的連接權值需要調整,因而學習速度快[7]。因此,選用RBF神經網絡來進行PID參數的在線整定,其控制結構如圖7所示。
文獻[8-9]系統論述了利用RBF神經網絡整定PID控制參數的方法,這里不再贅述。其中文獻[8]在MATLAB軟件中書寫了基于RBF神經網絡整定PID控制參數的S函數,設計了RBF神經網絡PID控制器的通用程序。這里將采用該方法設計艦炮隨動系統的位置環控制器。
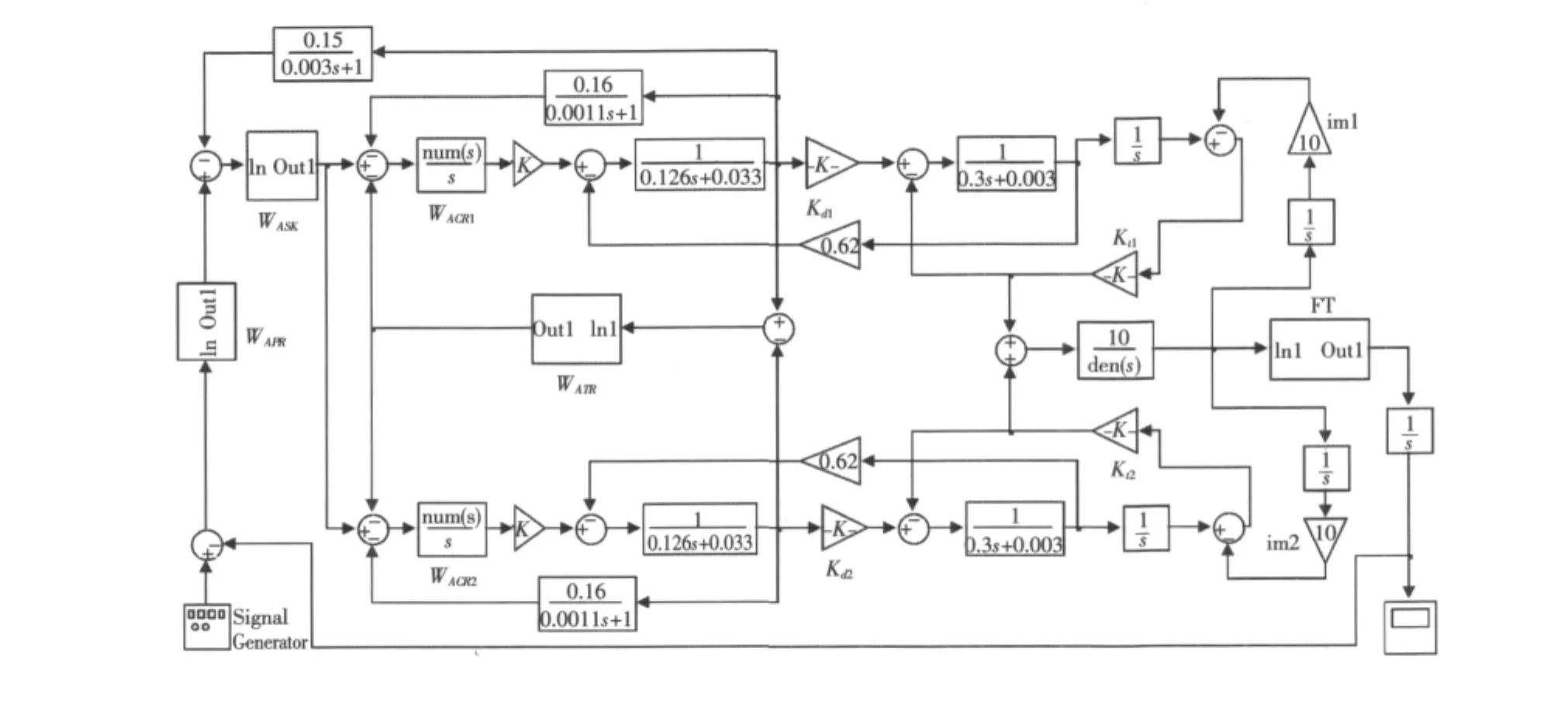
圖6 隨動系統仿真Fig.6 Simulation drawing of servo system
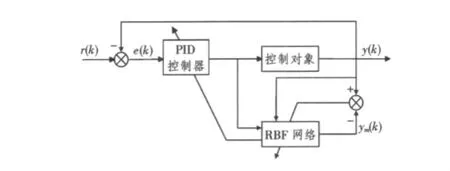
圖7 RBF神經網絡整定PID的控制結構Fig.7 Structure of the adaptive PID control system based on RBF NN
如何選擇合適的隱節點數,以使網絡學習達到要求的精度,目前還沒有成熟的辦法。用計算機選擇、設計、再檢驗是一種通用的手段。這里采用該方法經過大量的仿真比較發現,8個隱節點能滿足系統控制的需要,且效果較好。所以RBF神經網絡的最佳參數設置為:神經網絡的結構為3-8-1;采樣時間為ts=0.001 s;神經網絡的輸入矢量選為x(k)=[Δu(k),y(k),y(k-1)]T;PID 控制的比例系數KP、積分系數KI及微分系數KD的學習速率為η1=0.2;KP的初始值為5,KI的初始值為1,KD的初始值為2;神經網絡的學習速率為η=0.25;動量因子為α=0.07,β=0.01;設定隱層節點中心的初始值為3,隱層節點基寬參數的初始值為0.75,權系數的初始值為1。
4 仿真分析
以幅值為1 rad的階躍信號為輸入,運行傳統PID控制器控制下的艦炮隨動系統仿真模型,得到的系統響應曲線如圖8所示。
由圖8可見,由于身管振動的復雜性和非線性,使得整個隨動系統是時變和非線性的,參數固定的傳統PID控制器不能提供有效的控制,整個系統始終處于無法穩定的振蕩狀態。
以幅值為1 rad的階躍信號為輸入,運行RBF神經網絡PID控制器控制的艦炮隨動系統仿真模型,得到的系統響應曲線如圖9所示。
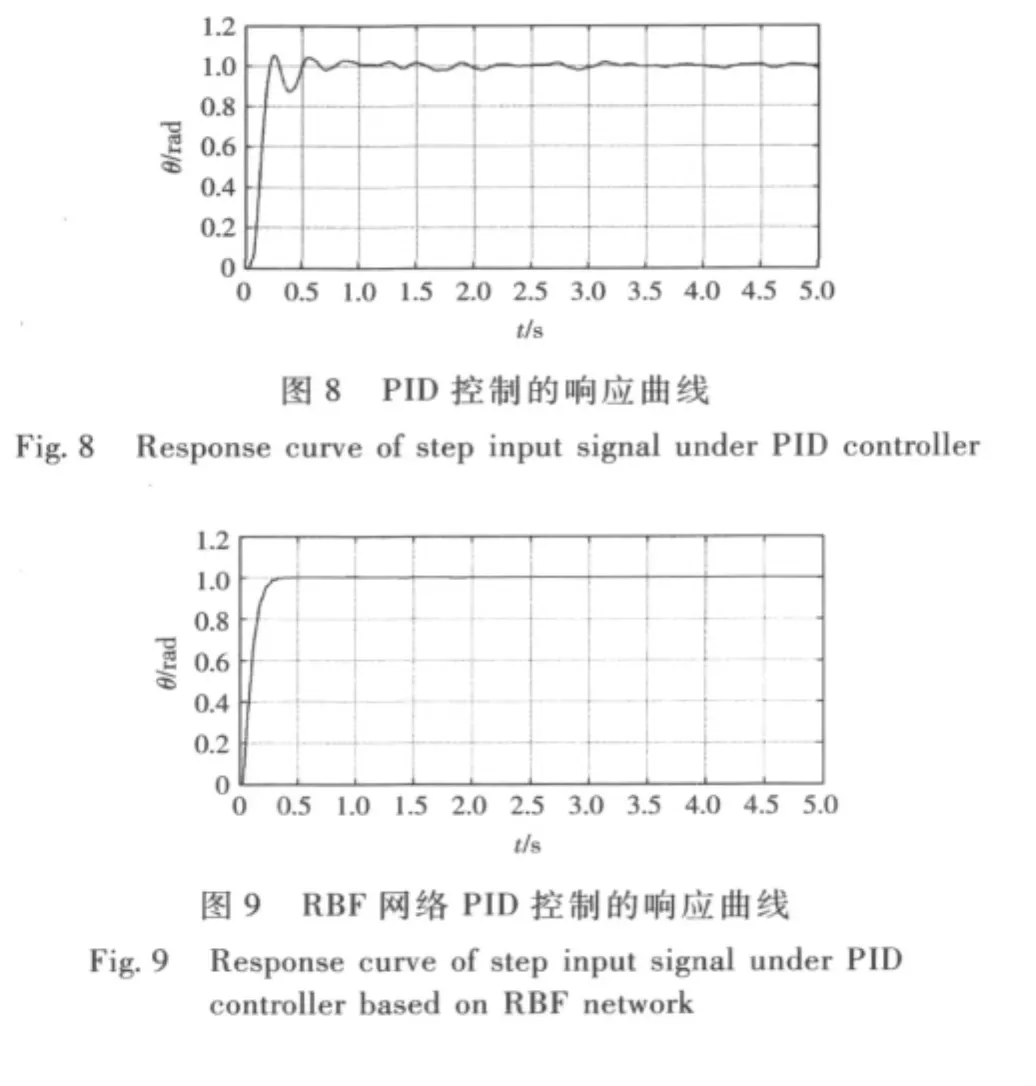
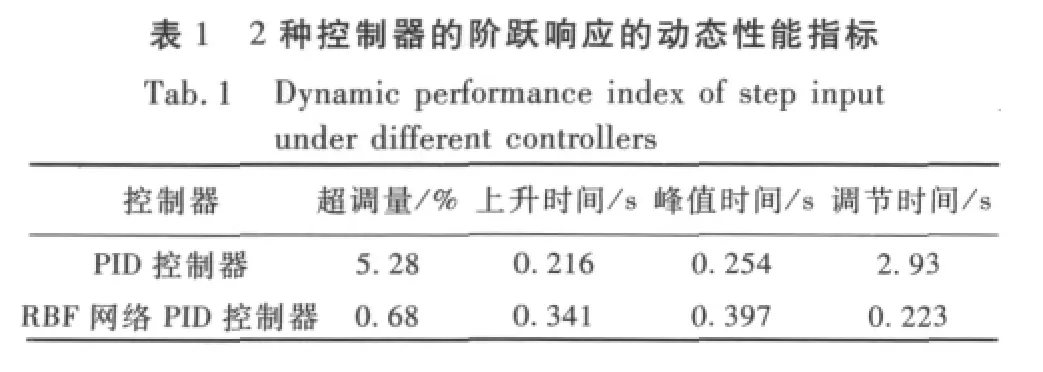
由圖9可見,由于RBF神經網絡可以在線整定PID控制器的參數,使得PID控制器能隨著系統的變化而調整。因此,系統能穩定運行,且具有較強的抗干擾性。2個控制器分別控制艦炮隨動系統的階躍響應的動態性能指標如表1所示。由表1可見,由于RBF神經網絡整定PID控制器參數是一個復雜的計算過程,所以它控制下的系統的階躍響應的上升時間和峰值時間稍慢于傳統的PID控制器,但其利用RBF網絡逼近非線性函數的能力能精確地調整PID參數,具有很強的魯棒性。
?
5 結語
仿真結果表明,本文提出的利用炮口角位移作為隨動系統位置環反饋信息的控制結構,將閉環控制擴展到了炮口,可以直接對炮口指向進行控制;為改進后的控制結構所設計的RBF神經網絡PID控制器能及時整定控制參數,能適應由于身管振動引起的系統變化。
[1]魏明義.火炮靜態檢測方法[S].國軍標,1997.
[2]王德石,歐陽光耀.火炮吸振器[J].火炮發射與控制學報,1999,(1):9 -14.
WANG De-shi,OUYANG Guang-yao.On artillery vibration absorber[J].Journal of Gun Launch & Control,1999,(1):9-14.
[3]忽麥玲,張光輝,衛平.雙電機驅動伺服系統的建模與分析[J].火炮發射與控制學報,2008,(2):93 -96.
HU Mai-ling,ZHANG Guang-hui,WEI Ping.Mode-ling and analysis of double-motor driven servo system[J].Journal of Gun Launch & Control,2008,(2):93 -96.
[4]GUSTAVSSON.Device for servo system with closed circuit[P].Untitled States Patent:4196380,1980 -04 -01.
[5]夏冰,編譯.減小火炮系統射彈散布的方法[J].兵工學報武器分冊,1987,(1).
[6]王德石.艦炮系統多剛體動力學分析[J].火炮發射與控制學報,1998,(4):1 -6.
WANG De-shi.Multi-body system dynamic analysis of naval gun[J].Journal of Gun Launch & Control,1998,(4):1-6.
[7]BARMISH B R,HOLLOT C V,KRAUS F J.Extreme point result for robust stabilization of interval plants with first order compensators[J].IEEE Transactions on Automatic Control,1992,37(6):707 -712.
[8]薛定宇.控制系統計算機輔助設計[M].北京:清華大學出版社,2006.383-390.
[9]劉金琨.先進PID控制 MATLAB仿真[M].北京:電子工業出版社,2004.43-45.
PID control based on RBF neural network of flexible gun-tube
TIAN Fu-qing1,LI Ke-yu1,LI Jin-wei2
(1.Department of Weaponry Engineering,Naval Univercity of Engineering,Wuhan 430033,China;2.The 713 Research Institute of CSIC,Zhengzhou 450015,China)
The traditional servo system can not provide the accurate control of the muzzle directionality because of the tube vibration,so aimed at the defect,a control structure which collected the feedback digital information of position loop from muzzle was put forward.A PID controller based on RBF neural network was designed for realizing the purpose of controlling the directionality of muzzle.Whose control effectivities were compared with effectivities of the traditional PID controller in simulation tests.
flexible tube;servo system;RBF neural network;SimMechancis
TJ391
A
1672-7649(2012)04-0093-05
10.3404/j.issn.1672-7649.2012.04.022
2012-02-09;
2012-03-01
田福慶(1962-),男,教授,主要從事武器系統仿真與總體設計研究。

