基于帝國主義競爭算法的切削參數優化

陳志楚，李 聰，張超勇

（1. 湖北汽車工業學院 電器信息與工程學院，十堰 442001；2. 華中科技大學 機械工程學院，武漢 430074）

0 引言

數控加工技術是現代自動化、柔性化及數字化生產加工技術的基礎與關鍵技術。切削參數的合理選擇與優化，直接關系能否合理地使用刀具與機床，對提高生產率，提高加工精度及表面質量，降低生產成本都有重要作用，是實現整個切削過程優化的關鍵。隨著各種新加工材料的不斷涌現，以及數控加工機床、加工中心和柔性制造系統的廣泛運用，在傳統的CAD／CAM系統中僅依靠個人經驗來確定切削參數己遠不能適應時代的發展。而運用現代切削理論、數學建模和模型分析方法尋求切削參數的最優組合，則是切削參數優化的一個重要發展方向，是實現高效數控加工技術的關鍵。

帝國主義競爭算法[15]最初是由Atashpaz-Gargari and Lucas于2007年在對基于人口數量最優化算法的著作中提出。在算法中， 每一個個體都被定義為一個國家，同時，所有的國家被分類為兩類，即帝國主義國家和殖民地。帝國主義國家為最初時人口數量最有優勢的國家，而剩下的國家即為殖民地。每個國家的力量被用來指明它的健康程度。在該算法的反復使用過程中，帝國之間相互競爭以獲得盡可能多的殖民地為目的。更有力量的帝國有更高的可能性去占領更多的殖民地，而力量薄弱的帝國將逐漸失去他們的殖民地。當所有的殖民地都被一個帝國占有時，該算法即為結束。在連續函數優化方面帝國主義競爭算法在效率和質量方面超過遺傳算法和粒子群優化算法。因此，本文引入帝國主義競爭算法求解切削參數優化問題。

1 切削參數優化的數學模型

切削速度、進給量和切削深度統稱為切削用量三要素。由于切削深度對刀具耐磨度的影響較切削速度和進給量要小，而且可根據工件余量和具體的加工要求來確定，這里視為已知量，不進行優化。因此，模型的設計變量包括切削速度v和進給量f，在銑削加工中，考慮的是每齒進給量fz。對于數控切削加工，因采用無級調速，所以切削參數是連續變量。切削參數優化問題的目標函數選擇生產率，表現形式為加工工時。

由于切削加工過程中包含多種實際約束，并且是非線性的。主要有：機床、刀具、夾具等所組成的工藝系統的加工能力；零件加工質量的要求；包括刀具壽命約束在內的經濟性約束等。所以，切削參數的數學模型是非線性、多約束的連續函數問題的優化。下面以銑削加工為例建立優化模型。

1.1 目標函數

引入以最大生產率為目標的切削參數數學模型。進行批量生產時，完成一道工序的銑削加工工時為[2～4]：

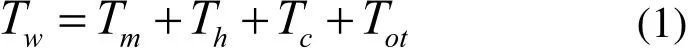
式中，Tw為完成一道銑削加工的總工時；Tm為工序的切削時間；Th為單工序銑削加工中由于刀具磨損導致的平均一道工序的換刀時間；Tc為工序之間的換刀時間；Tot為除換刀時間以外的其他輔助時間，包括工件的裝卸載時間、機床及刀具準備時間等。

工序切削時間Tm的表達式[2～5]：

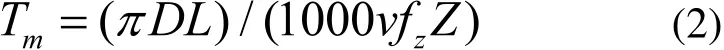
式中，D為刀具直徑；L為切削長度；v為切削速度；fz為銑刀每齒進給量；Z為銑刀齒數。

由于刀具磨損導致的平均一道工序的換刀時間Th的表達式：

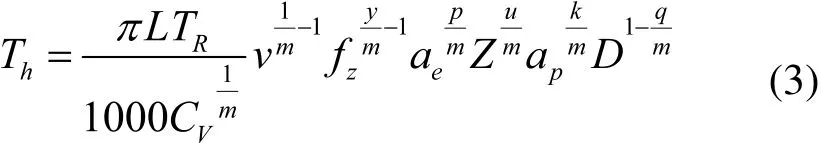
式中，L為切削長度；TR為刀具磨損的換刀時間；v為切削速度；fz為銑刀每齒進給量；ae為銑削寬度；Z為銑刀齒數；ap為銑削深度；D為刀具直徑；CV、m、y、p、u、k、q為銑刀的刀具耐用度系數。

綜合式(1)～式(3)，目標函數為：

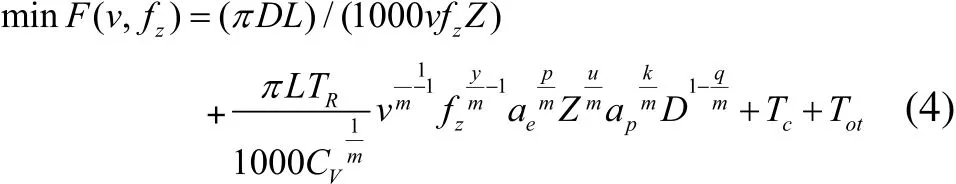
1.2 約束條件[2～5]

實際加工中的切削參數必須滿足上面提到的各類型約束，具體如下。

1.2.1 切削速度約束

數控機床需滿足切削速度約束，表達式如下：

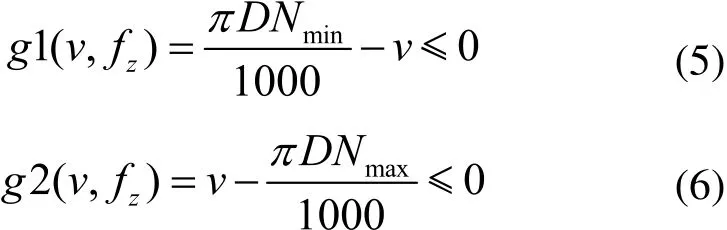
式中，Nmin、Nmax分別為主軸最低和最高轉速。

1.2.2 進給量約束

對銑削加工而言，每齒進給量滿足的約束條件如下：

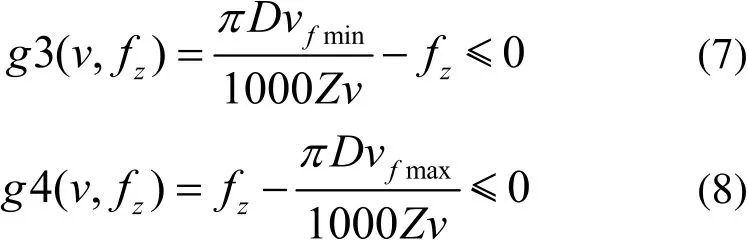
式中，vfmin、vfmax分別為機床最小和最大切削進給速度。

1.2.3 機床切削力約束

機床進給方向切削力應小于主軸最大進給力，表達式如下：

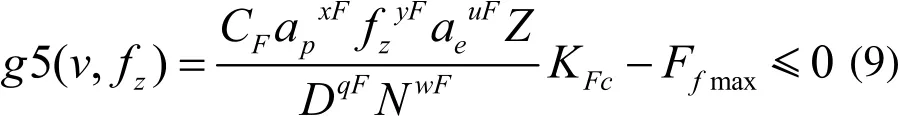
式中，Ffmax表示機床主軸的最大進給力；N為主軸轉速，CF、xF、yF、uF、qF、wF、KFc為切削力系數。

1.2.4 切削扭矩約束

切削扭矩不能超過主軸最大扭矩。表達式如下：

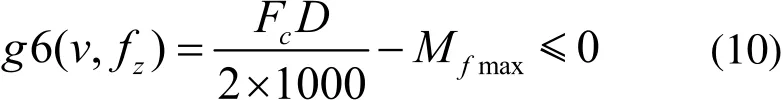
式中，Mfmax為機床主軸的最大扭矩。

1.2.5 機床功率約束

切削功率應小于規定的最大有效切削功率，表達式如下：

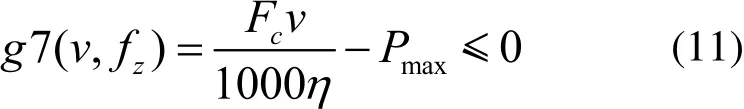
式中，?為機床功率有效系數；Pmax為機床最大有效切削功率。

1.2.6 粗糙度約束

零件還需滿足表面粗糙度要求，表達式如下：

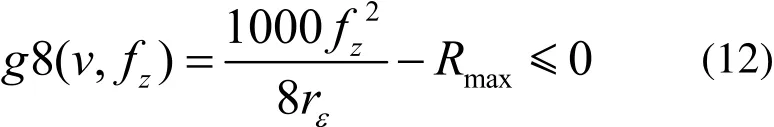
式中，r～為刀具的刀尖圓弧半徑；Rmax為表面粗糙度的最大值。

2 基于帝國主義競爭算法的切削參數優化

2.1 帝國主義競爭算法流程

帝國主義算法流程描述如下：

1）初始化帝國主義競爭算法的參數：Npop, Nimp

2）隨機生成Npop作為國家的人口數量。選擇Nimp最好的國家作為帝國并根據他們的能力規定他們的殖民地數量；

3）如果終止條件未得到滿足，則重復下列步驟；

4）內部位置交換；

5）帝國主義競爭；

6）淘汰弱小的帝國；

7）保留最終剩余的帝國，其適應度取值作為最優解。

流程圖如圖1所示。

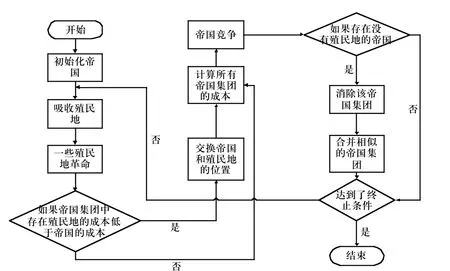
圖1 帝國主義競爭算法流程圖

2.2 帝國集團的初始化

在一個NVAR維的最優化問題中，一個國家即為一個1×NVAR的矩陣。該矩陣定義如下[16]：

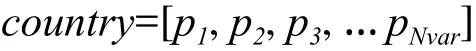
此處，Pi為被優化的變量。這些在國家屬性中的變量為浮點數。國家中的每個變量可以被理解為這個國家的社會政治屬性。在算法中幾時要求我們尋找到最小的成本值。每個國家的成本由變量所組成的函數f決定：

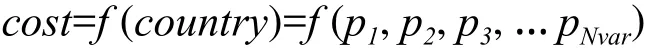
為了開始該最優化算法，必須初始化國家數量Ncountry.我們選擇Nimp個最優力量的國家來形成帝國集團。剩下的Ncol個最初國家作為這些帝國集團中的殖民地。

圖2 初始化帝國集團：帝國擁有的殖民地越多，它所代表的五角星越大

為了形成最初的帝國集團，殖民地依據各帝國的力量情況決定。即：一個帝國集團最初擁有的殖民地數量應直接與其力量所占比例相關。為了能按比例分配殖民地，每個帝國的成本被定義為：

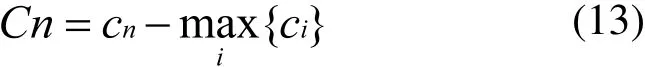
在這里，Cn為第n個帝國的成本。計算了所有帝國的成本后，帝國的相對力量定義為：

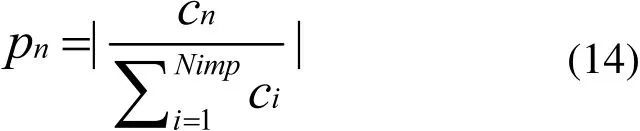
最初的殖民地的分配依賴于其所屬的帝國集團的力量。從而最初的殖民地分配為：

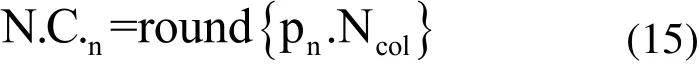
在這里，N.C.n為第n個帝國所擁有的殖民地數量。如圖2所示的初始化帝國集團，越大的帝國集團擁有更多的殖民地數量，同時，弱小的集團擁有較少的殖民地。在該圖中，帝國1組成最有力量的帝國集團，于是它擁有最多的殖民地數量。

2.3 帝國集團內部調整

為了實現吸收壯大的目的，帝國試圖去吸收它們的殖民地并使其成為帝國的一部分。更準確的說，殖民地沿著坐標軸向著帝國移動。移動過程如圖3所示。考慮一個二維最優化問題，殖民地在由文化和語言組成的坐標軸中被帝國吸收。殖民地將會不斷地向帝國移動，最終將使殖民地完全被帝國吸收。

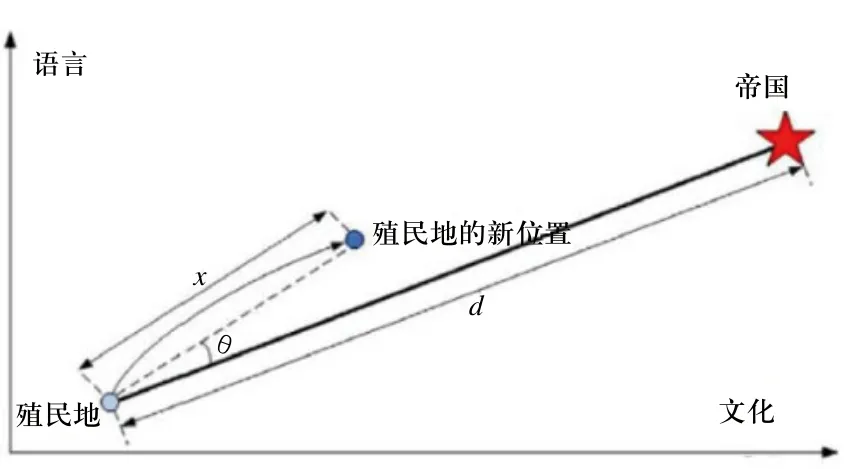
圖3 殖民地向其相關帝國的移動

在圖3中，x為一個服從均勻分布的隨機數x～U(0, β×d),在這里β為比1大的數，同時?為殖民地與帝國的距離。b>1將使殖民地從兩邊都離帝國更近。帝國對殖民地的吸收并不直接導致殖民地向帝國的移動。即是說，殖民地并不一定依照向量所示方向向帝國移動。為了更好模型化這個事實，引入一個隨機的角度作為移動的方向。在圖中顯示了新的方向。在該圖中，參數θ服從均勻分布。θ～U（-γ，γ），在這里γ為角度范圍。然而?和?是隨機的。在大多數情況中，我們將?設置為 2，?設置為π/4（Rad）。

革命是指在力量和組織結構的基礎方面在相對短時間內發生變化。在ICA的術語中，革命使一個國家的社會政治特征突然產生變化。即是說，與帝國的吸收不同，殖民地是隨機的在社會政治坐標軸中突然發生位置上的改變。圖3和圖4是在文化語言坐標軸中的革命過程。這種革命增加了該算法的搜索過程同時組織了國家形成早期的局部收斂。算法中的革命率顯示的是每個殖民地隨機改變它們位置的比例。一個較高的革命率會降低算法的搜索效果并降低收斂率。在我們的應用中，我們將革命率設定為0.3.即是指帝國集團中有30%的殖民地會隨機改變它們的位置。

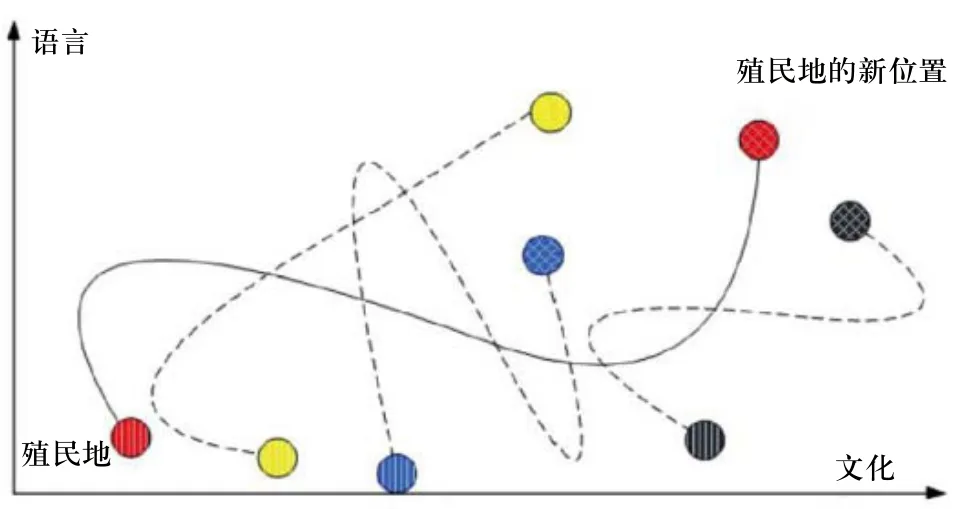
圖4 一個國家社會政治特征的突然改變

2.4 交換帝國和殖民地的位置

當殖民地向帝國移動的過程中，殖民地可能會到達一個成本比帝國要低的點。在這種情況下，帝國和殖民地即交換它們的位置。而后，算法將由在新位置的帝國吸收新位置的殖民地過程繼續下去。如圖5所示為帝國和殖民地交換位置的過程。在改圖中，最好的殖民地由深色表示，該殖民地比其帝國的成本要小。如圖6所示為殖民地和帝國交換位置后的狀態。

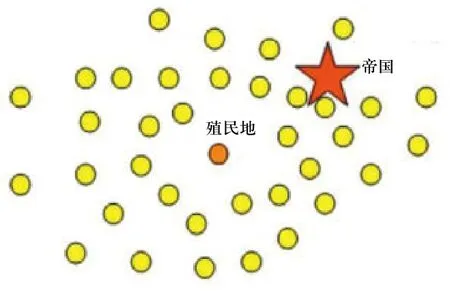
圖5 交換殖民地和帝國的位置

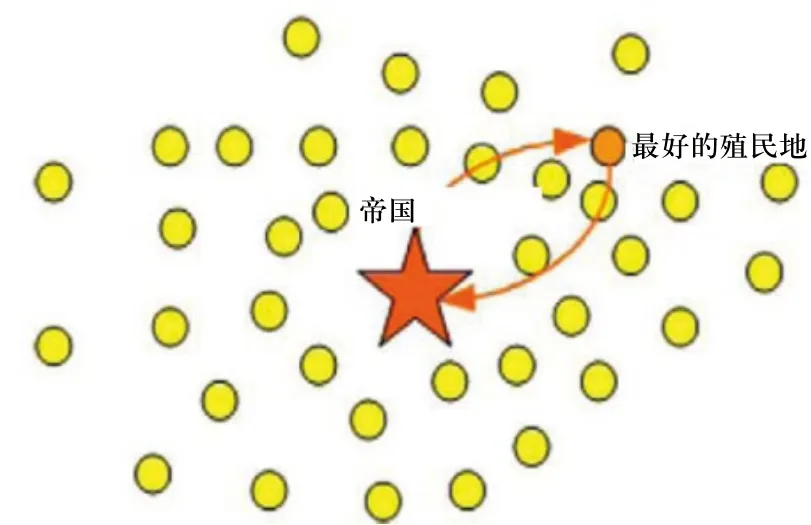
圖6 交換位置后的帝國和殖民地的狀態

在殖民地和帝國向著目標最小值移動的過程中，一些帝國可能會移動到相似的位置，如果兩帝國之間的位置要小于初始位置，它們將會合并為一個新的帝國集團。原帝國集團的殖民地將會成為新帝國集團的殖民地，同時新帝國的位置將由原帝國中二者之一的位置所決定。圖7和圖8顯示的合并過程。

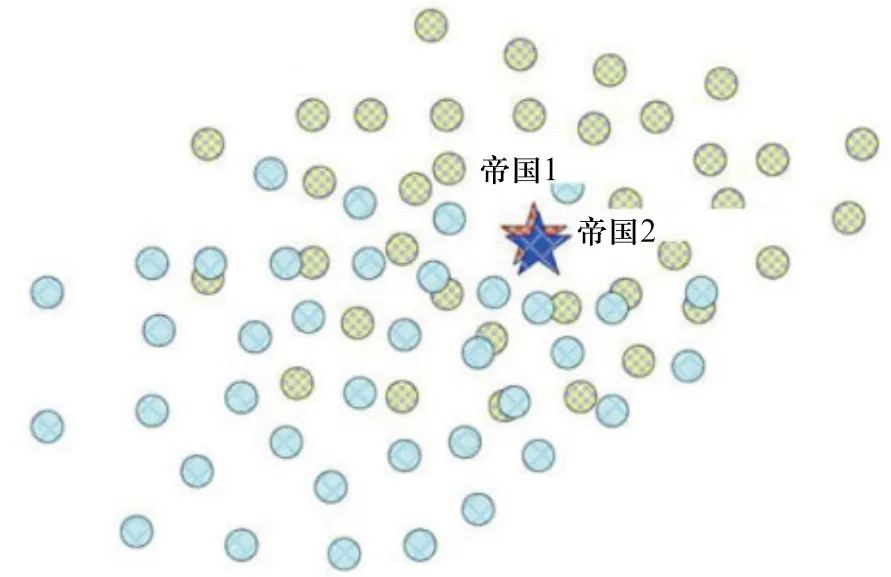
圖7 合并前的帝國集團

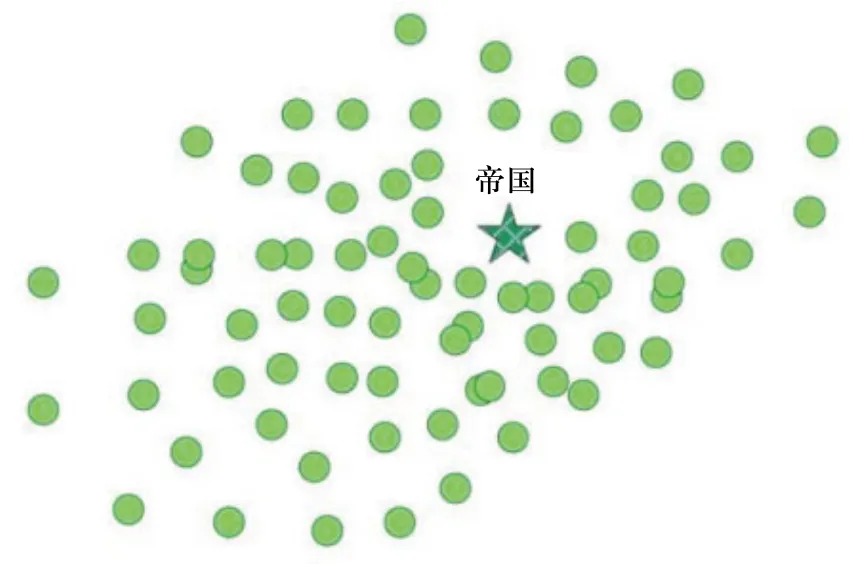
圖8 兩帝國合并后的狀態

2.5 帝國集團競爭

一個帝國集團的總力量主要由它的帝國力量所決定。可是殖民地的力量也對帝國集團的力量有影響。一個帝國集團的總成本由式（16）所決定[16]：

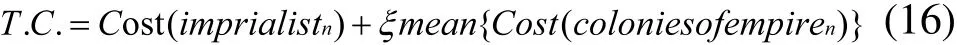
此處，T.C.為第n個帝國集團的總成本。ξ為一個較小的正數。ξ越大會使殖民地對帝國集團的影響越大。在大部分的情況下ξ取0.1被認為是最好的。

每個帝國集團都試圖占領并控制其他帝國集團的殖民地。帝國競爭過程中，強國將更強，弱國將更弱。帝國競爭一般先選出最弱帝國集團，并使其他帝國集團競爭去占領該集團。圖9顯示帝國競爭。在這個過程中，基于各自的力量，每個集團都有占領最弱集團的可能性。從另一個方面來說，最弱國不一定確定被最強國家占領，但是越強的集團占領弱集團的可能性越大。為了開始這個競爭過程，首先最弱的帝國集團的一個殖民地將被選出來，并確定每個國家占領的可能性。占領可能性Pp依據帝國集團的總力量所決定：

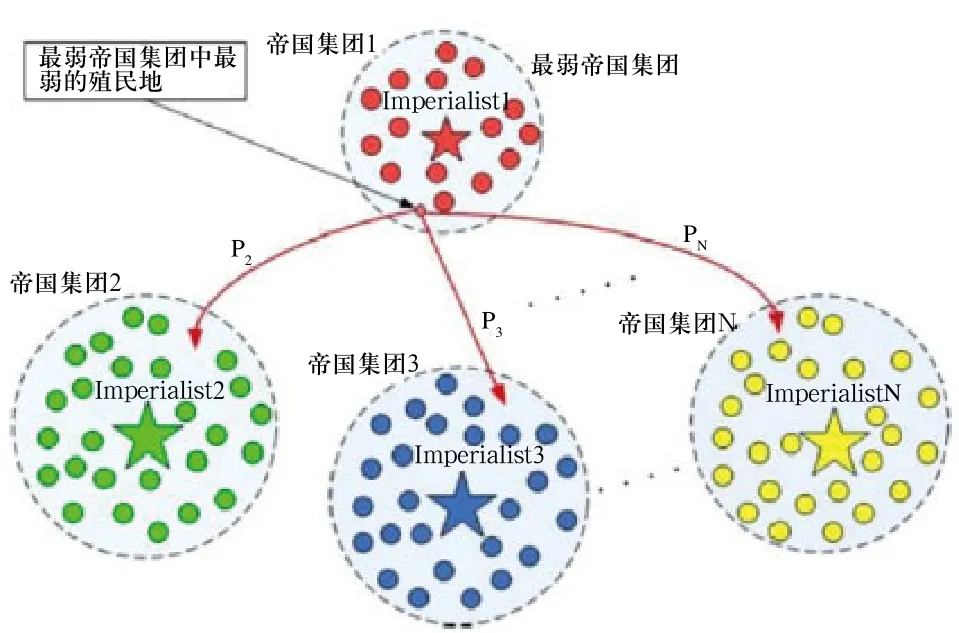
圖9 帝國競爭：帝國越有力量，越有可能占領最弱帝國集團的殖民地

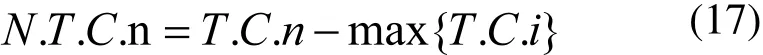
此處，T.C.n和N.C.n為第n個帝國集團的總成本和相對成本。依據相對成本，每個帝國的占領可能性由下式決定：

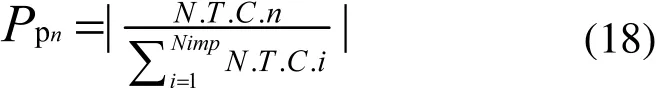
為了將在帝國集團中將上述的殖民地分類，我們引入如下向量P：

向量R是與向量P具有相同規格的向量，其元素服從均勻分布：

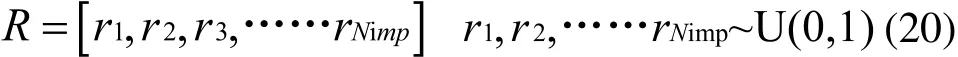
向量D由向量P減去向量R所得：

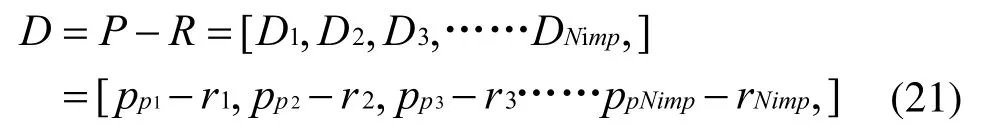
向量D中元素值最大的對應帝國集團即會占領上述的殖民地。

這樣選擇帝國集團的過程與遺傳算法中選擇母類的輪盤賭過程相似。但是這里的選擇方法比相關的輪盤賭過程要快。因為這個過程并不需要計算累積分布函數，并且選擇過程僅僅基于可能性的值。因此，帝國集團的選擇過程可以完全替換遺傳算法中的輪盤賭，并增加執行速度。上述步驟將會持續下去直至實現國家收斂并且達到成本最小的目標。不同標準可用來結束該算法。一種思想是設定最大迭代次數。或者當僅剩一個帝國集團時即結束該算法。

2.6 約束處理

依前所述，切削加工過程中存在各類非線性約束條件。ICA算法也是針對無約束優化問題的隨機尋優算法，因此，必須結合約束處理技術，才可用于解決切削參數優化問題。目前流行的約束處理技術主要是罰函數法[17]。文獻中考慮了粒子的歷史約束狀態，本文結合二者進行約束處理。針對本文數學模型，罰函數如公式(22)所示：

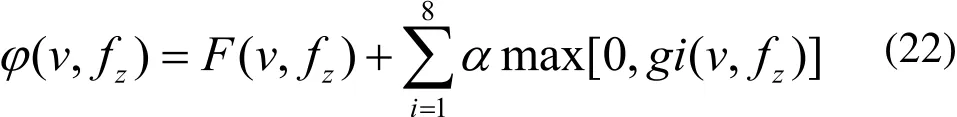
式中，α為罰因子。根據公式(22)來評價帝國和殖民地，如果當前帝國沒有違反約束條件，則以目標函數為評價標準，否則，根據罰函數來評價帝國。

3 實例分析與結果比較

3.1 模型與算法中的參數設置

3.1.1 切削參數優化模型中相關參數設置

前面引入參考文獻[2～4]中的模型，這樣便于比較結果，同理，也采用相同的實例。

刀具直徑：100mm；切削長度：159mm；切削深度：2mm；切削寬度：60mm。

銑刀齒數：4；

刀具刀尖直徑：1mm；

表面粗糙度最大值：3.2 ；

刀具磨損導致的換刀時間：600s；

主軸最低轉速：45轉/分 ；

主軸最高轉速：6000轉/分；

最小進給速度：3mm/s；

最大進給速度：8000mm/s ；

機床主軸最大進給力：8000N；

機床主軸最大扭矩：200N×m；

機床主軸最大有效功率：7.5Kw；

機床功率有效系數：0.8；

查切削用量手冊[5]得刀具耐用度系數：

Cv:1067 m:0.2 y:0.2 p:0.15 u:0.1 k:0.1 q:0.25；

切削力系數：

Cf:7900 xf:1.0 yf:0.75 uf:1.1 qf:1.3 wf:0.2 kfc:0.25。

3.1.2 ICA算法中的參數設置

ICA算法中，初始國家數量為20，其中帝國數量為5，殖民地數量為15；ξ為0.1，β設置為2，γ 設置為 π/4（Rad）；罰因子 α=1。

3.2 結果比較與分析

將ICA算法隨機測試20次，所得最好結果、平均值、最差結果和標準差結果與文獻[4]進行比較，如表1所示，其中PSO+LS代表采用局部搜索的PSO混合算法；PSO代表基本的PSO算法；SA代表模擬退火算法；Dynamic與Adaptive分別代表采用動態及自適應懲罰策略的遺傳算法。從表中可以看出，ICA算法最好解、平均解和標準差的值均優于其他算法，表明了ICA算法應用于切削參數優化問題的有效性和優越性。

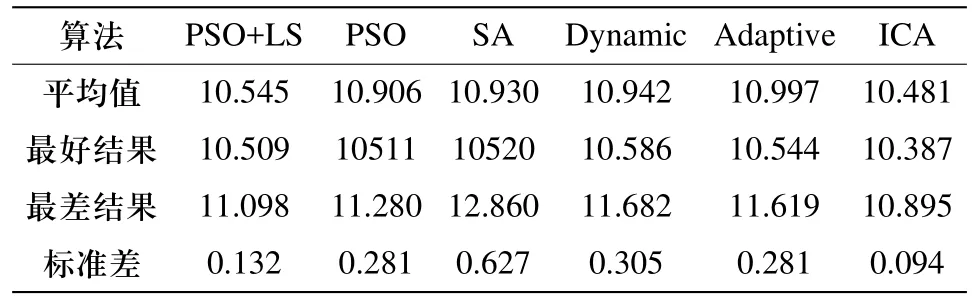
表1 不同算法隨機測試20次的統計結果

4 結論

本文在考慮機床加工和工件的實際約束的基礎上,建立以最大生產率為目標函數的銑削參數數學模型,然后應用帝國主義競爭算法對數控機床的銑削參數進行尋優,并進行了實例驗證。同時，在理論研究的基礎上，開發出相應的原型系統軟件，本文的研究內容和成果可為帝國主義競爭算法求解其他相似類型問題提供啟發和借鑒。

[1] 鄒云. 銑削加工切削參數只能選擇系統的研究與開發.2004.

[2] 凌玲, 黃豪, 胡于進等. 基于遺傳算法的多種切削方式集成參數優化[J]. 機械制造. 2009 (2): 43-47.

[3] 高亮, 高海兵, 周馳. 基于粒子群優化的切削參數優化算法研究[A]. 第五屆全球智能控制與自動化大會會議論文集(4)[C]. 2004: 2867-2871.

[4] 高海兵. 粒子群優化算法及其若干工程應用研究[D]. 華中科技大學出版社. 2004.

[5] 艾興, 肖詩綱. 切削用量簡明手冊. 第三版[M]. 北京: 機械工業出版社. 2004.

[6] Kennedy J, Eberhart R.C. Particle swarm optimization[C].Proc of IEEE Intl Conf on Neutral Networks, Perth,Australia, 1995: 1942-1948.

[7] 王凌, 劉波. 微粒群優化與調度算法[M]. 北京: 清華大學出社. 2008.

[8] K.E. Parsopoulos, M.N. Vrahatis. Particle Swarm Optimization Method for Constrained Optimization Problems[J]. Intelligent Technologies-Theory and Applications: New Trends in Intelligent Technologies, 2002, 214-220.

[9] Y. Shi et al., Cellular particle swarm optimization. Inform Sci. (2010), doi:10.1016/j.ins: 2010.05.025.

[10] 呂凱. 元胞自動機的研究及模型的建立[D]. 哈爾濱理工大學. 2007.

[11] 夏小翔, 曾建潮, 高慧敏. 基于元胞自動機的小生境微粒群算法[J]. 計算機工程與應用. 2007(11): 66-68.

[12] M. Tolouei-rad, I.M. Bidhend. On the optimization of machining parameters for milling operations. Intl. J. of Machine Tools & Manufacture. 1997, 37(1): 1-16 .

[13] C.Carlos. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms:a survey of the state of the art. Computer methods in applied mechanics and engineering. 2002. 191(11): 1245-1287 .

[14] Wassila Bouzid. Cutting parameter optimization to minimize production time in high speed turning. Journal of Materials Processing Technology. 161 (2005) 388–395.

[15] Esmaeil Atashpaz-Gargari,Caro Lucas.Imperialist Competitive Algorithm: An Algorithm for Optimization Inspired by Imperialistic Competition 1-4244-1340-0/07_c 2007 IEEE.

[16] Ebrahim Hosseini Nasab, Mohsen Khezri, Morteza Sahab Khodamoradi, Esmaeil Atashpaz Gargari, European Journal of Scientific Research,ISSN 1450-216X Vol.43 No. 4 (2010): 495-506.

[17] 何郁波, 馬昌鳳, 田亞娟, 非線性互補問題的罰函數法,1001-7437(2005)06-61-03.

[18] P. Padilla, B. Anselmetti, L. Mathieu, M. Raboyeau,Productionm’ ecanique Dunod, 1986.

[19] J. Paulo Davim, A note on the determination of optimal cutting conditionsfor surface finish obtained in turning using design of experiments, JMPT 116 (2001) 305–308.

[20] J. Paulo Davim, Design of optimization of cutting parameters for turning metal matrix composites based on the orthogonal arrays, JMPT 132(2003) 340–344.