橢球上三維均勻分布的參數估計

張莉莉， 魯富榮

（1．山西農業大學文理學院，山西太谷 030801；2．山西大學商務學院理學系，山西太原 030031）

0 引 言

均勻分布是概率論中的一個常用分布。目前，有關區間［a，b］上一維均勻分布的研究已有很多成果，對于二維均勻分布的研究，其成果主要有矩形區域和圓內二維均勻分布的參數估計及區域面積的估計［1－3］。文獻［4－5］研究了長方體上的三維均勻分布問題，文獻［6］考慮了n維球內均勻分布的參數估計問題。文中主要研究橢球上三維均勻分布的參數估計問題，并給出了未知參數與橢球體積的矩估計及參數的最大似然估計和區間估計。

1 定義及引理

定義1 設Ω是空間上的有界區域，其體積為V。若三維隨機變量（X，Y，Z）有概率密度

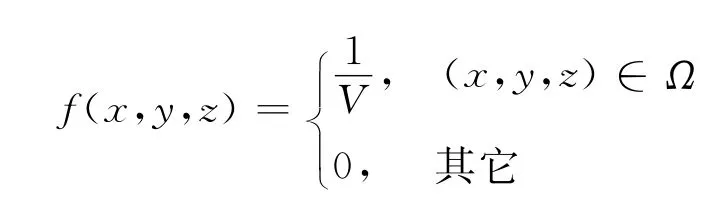
則稱（X，Y，Z）在Ω上服從均勻分布。注1：當

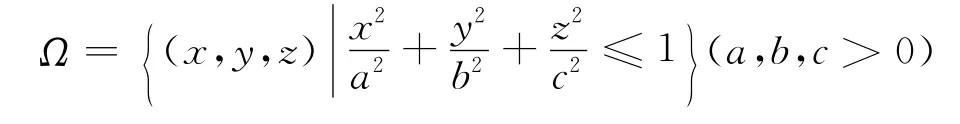
引理1 設三維隨機變量（X，Y，Z）為來自球x2＋y2＋z2≤a2上均勻分布的總體，a＞0未知，（X1，Y1，Z1），（X2，Y2，Z2），…，（Xn，Yn，Zn）為其n個樣本，（x1，y1，z1），（x2，y2，z2），…，（xn，yn，zn）為樣本值，則球半徑a的最大似然估計量為

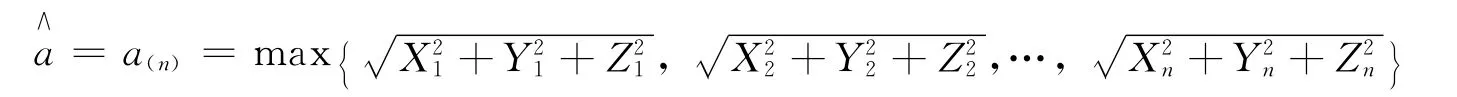
證明：隨機變量（X，Y，Z）的概率密度函數為

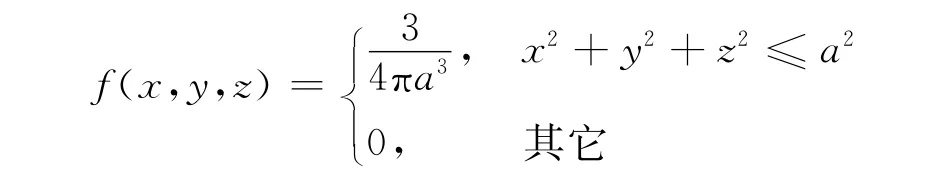
令

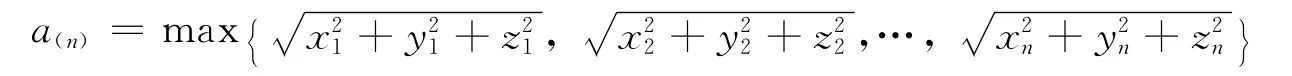
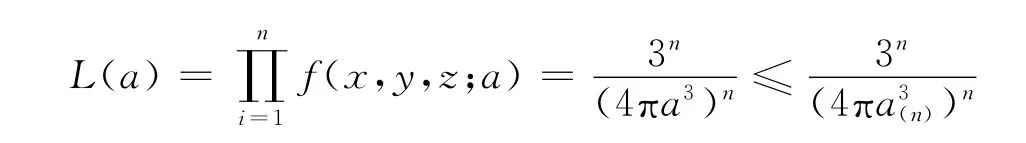
即L（a）在a＝a（n）時，取到最大值故a的最大似然估計值為

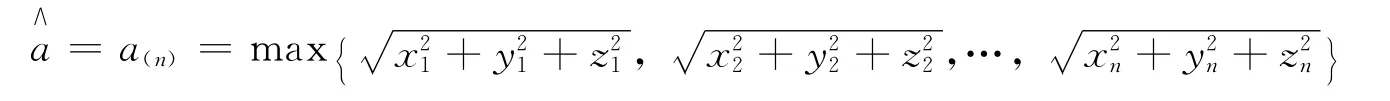
a的最大似然估計量為

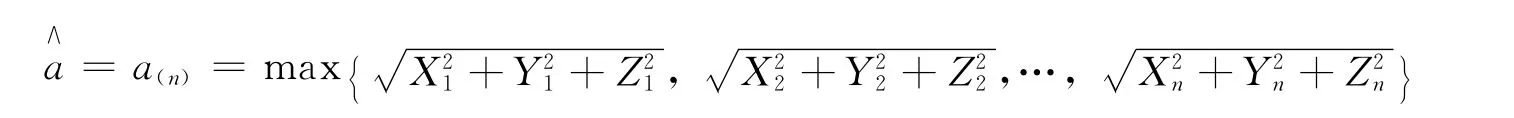
注2：本引理用另一方法證明了文獻［7］中n＝3的結論。

引理2［7］設隨機變量（X，Y，Z）在球x2＋y2＋z2≤a2上服從均勻分布，a＞0未知，則a的置信水平1－α的置信區間為且此區間為用作為樞軸量建立的置信水平為1－α的最短置信區間，其中a∧為a的最大似然估計。

2 參數的矩估計

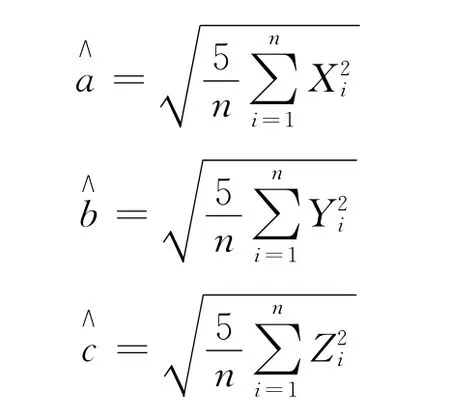
橢球體積V的矩估計量為

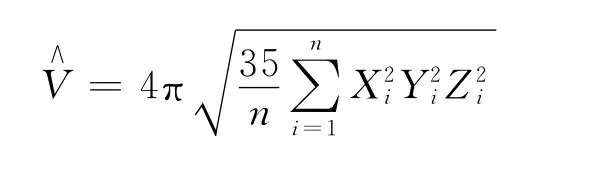
證明：隨機變量（X，Y，Z）的概率密度函數為

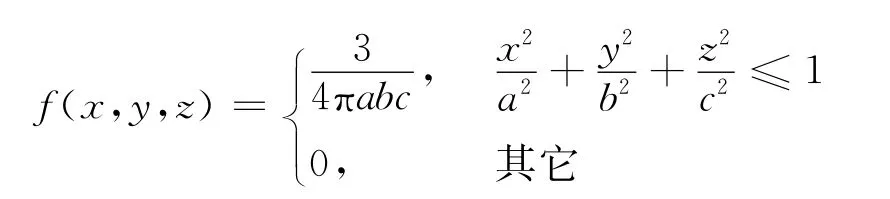
作廣義球坐標變換

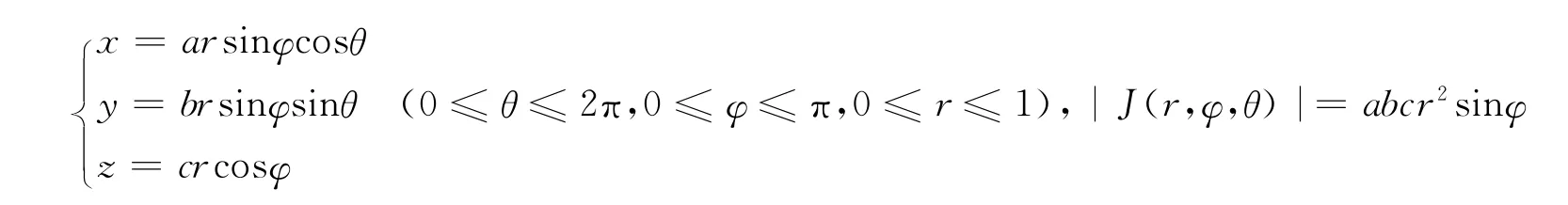
則X，Y，Z的2階原點矩分別為：

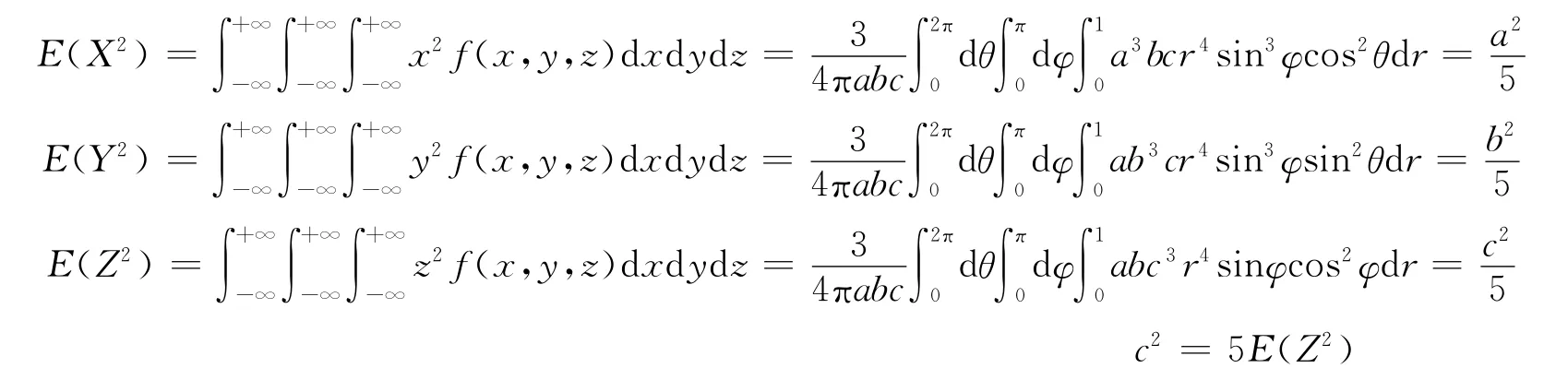
即a2＝5E（X2）b2＝5E（Y2）

X，Y，Z的6階混合原點矩為

即

a2b2c2＝315E（X2Y2Z2）

所以，橢球半軸長a，b，c的矩估計量分別為：

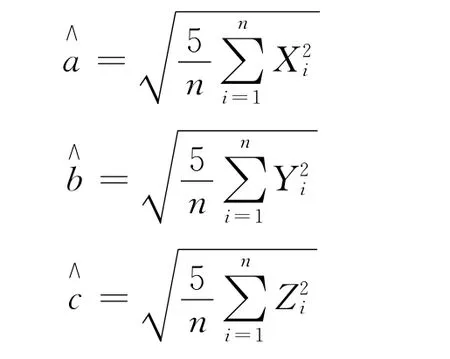
橢球體積V的矩估計量為

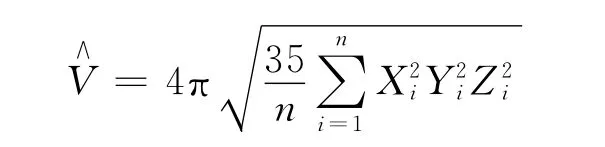
注3：當a＝b＝c時，可得服從球x2＋y2＋z2≤a2上均勻分布的三維隨機變量，球體積V＝的矩估計量為

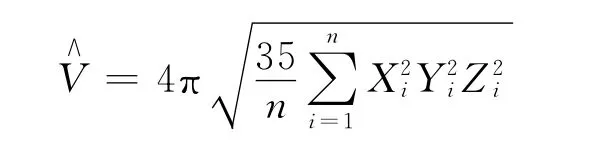
3 參數的最大似然估計

定理2 設三維隨機變量（X，Y，Z）在橢球上服從均勻分布，令U＝X，，則隨機變量（U，V，W）服從球u2＋v2＋w2≤a2上的均勻分布。

證明：隨機變量（X，Y，Z）的概率密度函數為

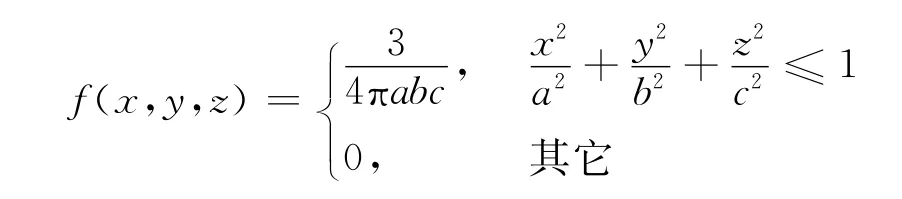
作變換

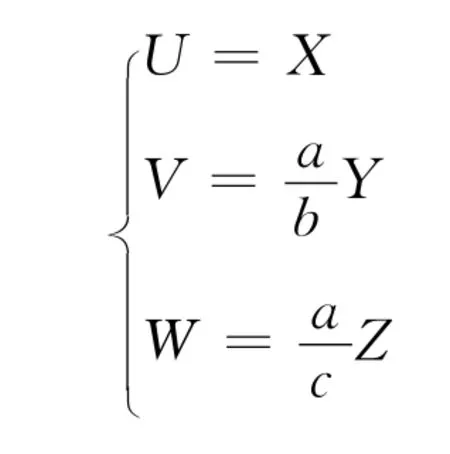
即

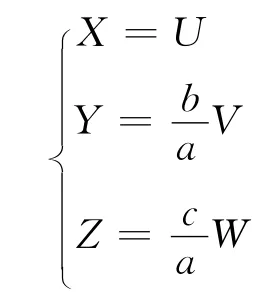
則三維隨機變量（U，V，W）的概率密度函數為

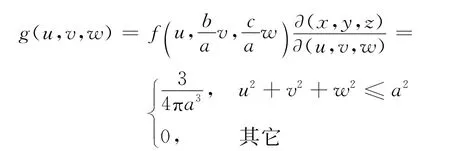
所以，三維隨機變量（U，V，W）服從球u2＋v2＋w2≤a2上的均勻分布。

定理3 設三維隨機變量（X，Y，Z）為來自橢球上均勻分布的總體，（X1，Y1，Z1），（X2，Y2，Z2），…，（Xn，Yn，Zn）為來自這一總體的n個樣本。若橢球的半軸長之比＝k2已知，則a的最大似然估計量為

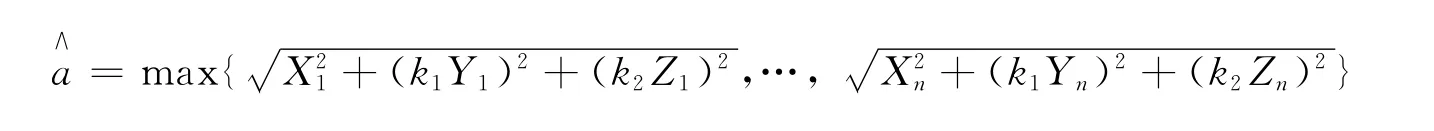
b的最大似然估計量為

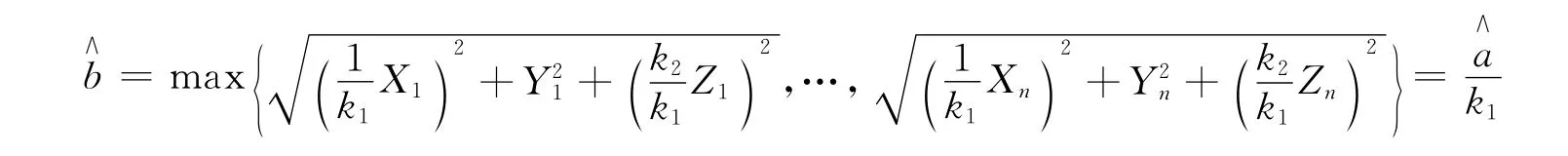
c的最大似然估計量為

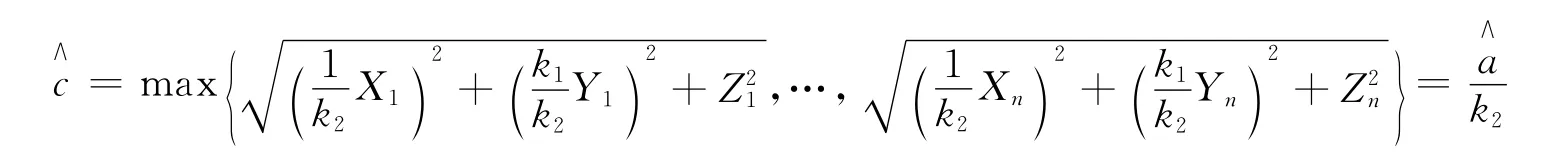
證明：由引理1和定理2證之。

4 參數的區間估計

定理4 設三維隨機變量（X，Y，Z）在橢球上服從均勻分布，若橢球的半軸長之比已知，則a，b，c的置信水平為1－α的置信區間分別為且這些區間分別為用作為樞軸量建立的置信水平為1－α的最短置信區間。其中分別為a，b，c的最大似然估計。

證明：由引理2和定理3易證之。

綜上所述，我們得到了橢球上三維均勻分布未知參數及橢球體積的矩估計，在橢球半軸長之比k1，k2已知的條件下，還得到了參數的最大似然估計和區間估計。當這個比值未知時，可先求出k1，k2的矩估計量，然后得參數的兩步估計［7］。另外，文中結論不難推廣到n維橢球上均勻分布的情況。

參數估計問題是統計推斷的一類基本問題，除點估計與區間估計以外，還可研究參數的Bayes估計，如文獻［8］討論了Poission分布、二項分布、幾何分布的Bayes估計，對于均勻分布參數的Bayes估計有待進一步考慮。

［1］ 魯富榮，張莉莉．橢圓上二維均勻分布的參數估計［J］．山西大同大學學報，2010，26（4）：6－8．

［2］ 劉兆君．二維均勻分布矩形區域面積的估計［J］．大學數學，2007，23（4）：155－159．

［3］ 王志祥．圓內二維均勻分布的參數估計［J］．大學數學，2008，24（2）：150－152．

［4］ 劉兆君，呂永敬．三維均勻分布長方體域邊長的聯合置信域［J］．山東師范大學學報，2007，22（4）：132－133．

［5］ 陳光曙．長方體上均勻分布的密度函數［J］．純粹數學與應用數學，2009，25（4）：721－724．

［6］ 王志祥．n維球內均勻分布的參數估計［J］．純粹數學與應用數學，2009，25（4）：789－793．

［7］ 王松桂，史建紅，尹素菊，等．線性模型引論［M］．北京：科學出版社，2004：5．

［8］ 邢蕾，趙鵬飛．Q－對稱熵損失函數下幾何分布參數估計［J］．長春工業大學學報：自然科學版，2008，29（6）：614－616．