單相LCL并網逆變器雙電流閉環控制仿真研究

王 東，薛士龍，宗艷玲

（上海海事大學 物流工程學院，上海201306）

0 引 言

進入21世紀，開發新能源和發展可再生能源，實現經濟可持續發展，已成為人類社會的共識。逆變器是光伏系統的核心，同時也是其它新能源如風能開發技術的關鍵所在，因此研究逆變器的并網控制具有重大意義和重要的應用前景。入網電流的總諧波失真（total harmonic distortion，THD）和并網發電功率因數（power factor，PF）是衡量并網發電電能質量的2項重要指標。因此，常用濾波器來濾除并網逆變器輸出中包含的高頻PWM諧波，以滿足諧波標準［2］。

目前，太陽能發電逐漸向大功率方向發展，風能發電更是出現了兆瓦級以上的容量，采用較低的開關頻率，傳統的L濾波已經不能滿足要求，很多專家學者提出了LCL濾波技術。LCL濾波器對高頻分量呈高阻抗特性，對高頻諧波電流可起到很大的衰減作用［3］，選取較小的電感值就能實現較好的濾波效果，且系統動態性能好［3］。

但是LCL濾波器是一個三階系統，易引起輸出振蕩；對并網逆變器電流控制的設計有更高要求。本文采用并網電流和電容電流雙閉環的控制策略，既可減少諧振，又能保證高的并網電流功率因數。

1 濾波器參數設計

采用LCL濾波器的單相光伏并網逆變器主電路結構如圖1所示，其中Ud為直流側輸入電壓，S1－S4為IGBT功率開關管，Ui（s）為未經濾波的逆變器輸出電壓，i1為逆變器輸出電流，ic為電容支路電流，i2為并網電流，逆變橋采用單極性SPWM技術進行控制。當開關頻率遠高于輸出濾波器的截止頻率時，逆變橋可等效為比例環節KPWM。忽略濾波電感的電阻和電容的寄生電阻。

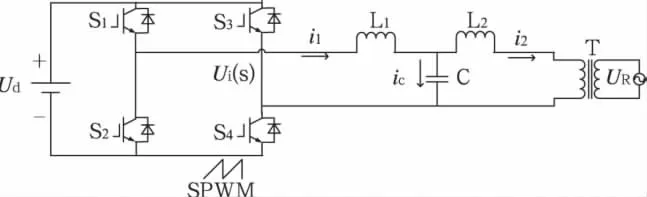
圖1 單相LCL并網逆變器主電路

本文先建立一個3 kW/220 V的單相并網逆變器模型。開關頻率設定為16 kHz，直流側電壓取為350 V，輸出頻率為50 Hz，根據電流紋波計算L1＋L2，在低頻時LCL濾波器可簡化成電感值L為的單電感濾波器，故可用單電感L近似計算L1＋L2的值［4］。

式中，D（t）為占空比，fc為開關頻率。由于開關頻率遠大于工頻頻率，可得：

代入數值可得：

實際取L＝2.4 mH，不同文獻對L2/L1取值不同，本文選擇L1＝2 mH，L2＝0.4 mH。

電容參數受系統容量的限制。電容值的增加會降低系統的功率因數，通常在選擇電容參數時，電容參數對系統功率容量的影響要小于10%。本文取為5%。

代入數值得：C＝9.87μF，本文取C＝10μF。

2 電流雙閉環控制

2.1 控制方案分析

如果對LCL并網逆變器采用并網電流直接控制，其控制框圖如圖2所示。

圖2 i2直接閉環控制框圖

由圖2可得并網電流i2與PI控制器輸出I（s）的傳遞函數為：

代入參數可得：

加入電容電流閉環控制，系統結構框圖如圖3所示：

圖3 并網電流和電容電流雙閉環控制系統結構框圖

由圖3可得并網電流i2與PI控制器輸出I（s）的傳遞函數為：

令K＝1，代入參數可得到：

分別畫出式（10）和式（12）的幅頻特性曲線，如圖4所示。

圖4 幅頻特性曲線

由圖4可以很明顯看出，加入了電容電流內環控制后，諧振尖峰得到了很好的抑制。可見，采用電容電流內環可以增加系統阻尼，從而抑制諧振尖峰，增強系統穩定性。

2.2 控制參數計算

由圖3可以得到電容電流內環的傳遞函數為：

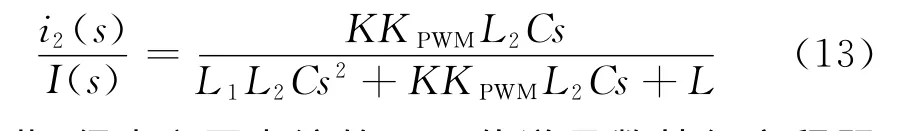
由此，得出入網電流的開環傳遞函數特征方程阻尼系數為：

工程中通常為了兼顧系統的阻尼和動態特性，一般取ζ＝0.707。將L1，L2，C，KPWM的值代入上式可得到k＝0.14。

本文中外環控制采用PI控制器，PI控制器的參數工程整定法比較多，本文采用振蕩指標法。

文獻［6］中詳細介紹分析了這種PI參數整定方法。本文根據文獻［6］中的方法計算得到PI的參數為：KP＝0.5，Ki＝1 200。

由于電網電壓并不是固定不變的，所以為了克服電網電壓擾動對LCL濾波器的影響，增加了電網電壓的前饋環節，根據文獻［6］的方法，設定了電網電壓前饋函數Gn＝1/KPWM。這樣可大大減小電網電壓變化對入網電流的干擾。

3 系統仿真分析

為了驗證理論分析的正確性和電流雙閉環控制系統的穩定性及動態性能，在 Matlab R2008/Simulink仿真環境下進行了仿真。根據前面算出的系統參數，搭建的仿真模型如圖5。

圖5 逆變器電流雙閉環控制仿真模型

仿真中，輸入電壓為350 V，開關頻率設定為16 kHz，SPWM調制比設定為0.8，參考電流為逆變器額定輸出電流19.3 A，圖6為電網電壓與并網電流放大10倍的波形。

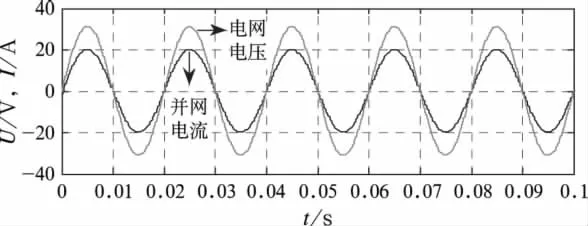
圖6 電網電壓與并網電流仿真波形

由圖6可以看出，使用雙閉環電流控制能控制輸出電流跟蹤電網電壓，實現了輸出電流和電網電壓的同頻同相，接近單位功率因數并網。從仿真波形還可以看出，通過濾波器濾波的并網電流諧波含量顯著減小，LCL濾波器的效果很好。圖7對并網電流前五個周期的仿真波形進行傅立葉分析，THD＝0.69%，仿真效果比較好。

圖7 并網電流的FFT分析

為了觀察系統的動態響應特性，對逆變器由滿載到半載的突變進行動態仿真，其仿真波形如圖8所示。

圖8 逆變器工作從滿載到半載的動態仿真波形

圖8（a）中的波形顯示了逆變器正常工作時，負載發生突變后，系統能夠恢復穩定運行；圖8（b）的放大波形顯示：在0.055 s時刻負載發生突變，0.057 s時刻逆變器在半載情況下穩定運行。系統在負載突變時的過渡時間為0.002 s，為0.1個周期的時間，可見系統具有較好的穩定性。

4 結 論

LCL濾波器是一個三階振蕩系統，采用并網電流直接閉環控制存在諧振尖峰，易造成系統的不穩定。本文采用了并網電流和電容電流的雙閉環控制，加入電網電壓前饋控制的控制策略。通過3 kW逆變器的設計和仿真驗證，該控制策略可以有效地抑制諧振，提高系統穩定性，系統具有優良的動靜態性能。仿真結果還表明并網電流的諧波總量小于5%，達到并網電流標準要求。因此，電流雙閉環控制方案是可行的。

［1］ 鄭詩程.光伏發電系統及其控制的研究［D］.合肥：合肥工業大學，2004.

［2］ 吳衛民，劉松培，何遠彬，耿 攀.單相LCL并網逆變器電流控制綜述［J］.電源學報，2011，3：51－57.

［3］ 劉 飛，徐鵬威，陳國強，等.基于LCL濾波器的三相光伏并網控制系統研究［J］.太陽能學報，2008，29（8）：965－970.

［4］ 張 濤.單相LCL濾波器的并網逆變器控制的研究［D］.秦皇島：燕山大學，2010.

［5］ 王章權.瞬時電流跟蹤控制光伏并網技術［J］.電源技術，2007，20（8）：648－650.

［6］ 徐志英.并網逆變器電流控制技術的研究［D］.南京：南京航空航天大學，2009.