單相三電平PWM整流器電流解耦控制方法
黃嘉鵬,張 斐
(西南交通大學 電氣工程學院,四川 成都 610031)
0 引 言
與傳統不控整流或相控整流方式相比,PWM整流方式具有功率因數高、可實現能量雙向傳輸等優點,是一種真正的“綠色”電能變換[1]。
PWM整流器的控制目標包括網側輸入電流和直流輸出電壓,且主要根據輸入電流正弦度以及是否與輸入電壓同頻同相位來評估整流器性能的優劣。然而由于網側輸入電壓波動,PWM整流器的電流控制器設計困難。直流功率變換器可以設計實現無穩態誤差的電流控制器,但若交流功率變換器采用同樣的設計方法,網側輸入電流幅值和相位均會產生較大的穩態誤差[2]。
文獻[3]通過引入一個虛擬輸入電流,提出了單相三電平PWM整流器基于dq坐標系的電流控制策略,但電流內環需要兩個PI調節器,控制較為復雜,且PI參數不易整定。文獻[2]利用數學推導消除了虛擬輸入電流,一定程度簡化了控制系統,但電流內環仍有兩個PI調節器。本文以單相三電平中點箝位(Neutral Point Clamped,NPC)PWM 整流器為研究對象,提出了基于dq坐標系的電流解耦控制策略。該控制策略消除了有功電流與無功電流的相互影響,并使電流內環控制不依賴于PI控制器,能夠實現網側輸入電流正弦化并使系統具有高功率因數。
1 單相三電平NPC PWM整流器
單相三電平NPC PWM整流器的主電路如圖1所示,它由8個IGBT模塊構成兩組對稱的橋臂,每組橋臂各有兩個箝位二極管,C1、C2分別為兩個直流側支撐電容,Ls、Rs分別為變壓器二次側漏感和漏電阻。為便于分析,忽略漏電阻Rs,定義開關函數如下:
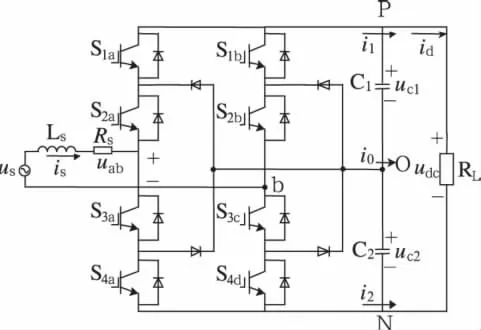
圖1 單相三電平NPC整流器

由式(1)、(2)可以看出SA和SB均具有三種工作狀態。以a橋臂為例,當開關函數SA=1、0、-1時,uao分別對應udc/2、0、-udc/2。因此,單相三電平 NPC整流器具有3×3=9個工作模式。輸入端電壓uab如圖2所示,由單相三電平NPC整流器的9個工作模式可知uab有5個臺階,每個臺階對應一個或多個工作模式。
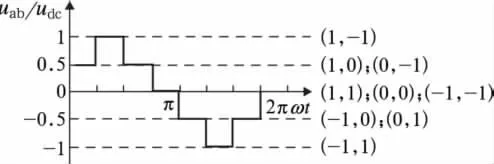
圖2 輸入端電壓uab與工作模式對應關系示意圖
假設開關為理想器件,且換相過程中無能量損失,則單相三電平NPC整流器交流側與直流側瞬時功率相等。對圖1中主電路的交流側回路采用KVL可得:

2 控制策略
PWM整流器一般采用電壓外環、電流內環的雙閉環控制策略[4]。圖3所示為PWM整流器的雙閉環控制框圖,參考電壓與直流輸出電壓udc比較的誤差信號送入PI調節器,其輸出作為參考電流的幅值。通過鎖相環(PLL)檢測輸入電壓us獲得參考電流的頻率和相位,從而保證了和us同頻同相位。因此,電流內環控制的目的是要保證輸入電流is能夠很好地跟蹤參考電流,從而實現網側輸入端的單位功率因數。

圖3 PWM整流器雙閉環控制框圖
2.1 變量定義
單相PWM整流器中,網側輸入電壓us、輸入電流is和整流器輸入端電壓uab可分別定義為[2]:
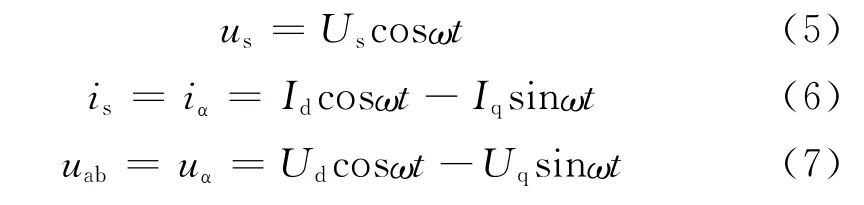
式中:Id、Iq分別為輸入電流的有功、無功分量的幅值;Ud、Uq分別為整流器輸入端電壓d軸、q軸分量的幅值。由于單相系統中只有一個輸入電流變量,dq變換不能直接應用[2]。為了解決這個問題,需引入一個虛擬輸入電流變量iβ。如前所述,參考電流的頻率和相位通過鎖相環(PLL)檢測輸入電壓us獲得,將定義為,同時假設β軸上的電流參考分量與同頻率,且滯后其π/2,可得:

由式(6)可知,網側輸入電流is分解為d軸上的有功分量和q軸上的無功分量。顯然,PWM整流器的控制目標是使無功分量為0。再將式(8)、(9)進行坐標變換可得輸入電流有功分量的參考值,即:

2.2 整流器數學模型
將式(6)和(7)代入式(3),令等式中正弦項系數和余弦項系數分別相等,則可推導出基于dq坐標系單相三電平NPC PWM整流器的平均值數學模型為:
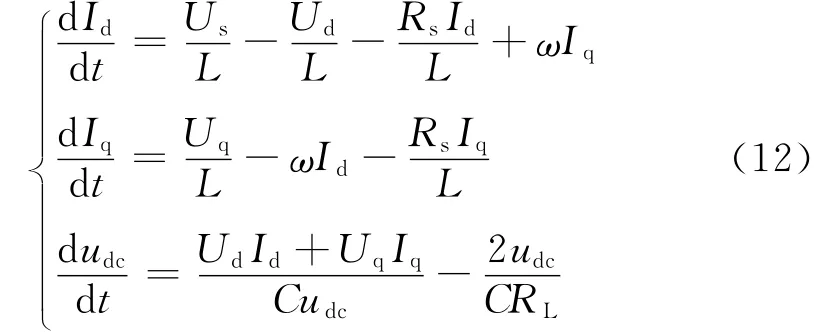
由式(12)可知,PWM整流器中有三個狀態變量Id、Iq、udc,兩個輸入變量Ud、Uq,通過控制Ud、Uq來控制Id。但在狀態方程中Id、Iq并不獨立,彼此之間存在耦合關系,因此傳統的線性控制方法很難達到理想的控制性能。
2.3 電流解耦控制策略
為了提高單相三電平NPC PWM整流器電流內環的控制性能,簡化控制系統設計,電流內環采用線性解耦控制。其控制思想是:引入新的輸入變量、,通過兩個獨立輸入變量使得Id、Iq轉化為解耦的線性關系。則新的輸入變量、與狀態變量之間的關系可描述為:
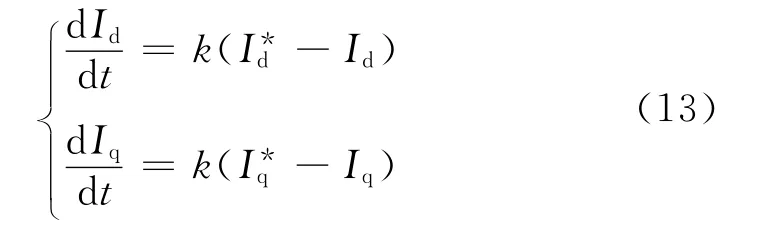
將式(13)代入(12)可得:

忽略Rs大小,由上式可得:
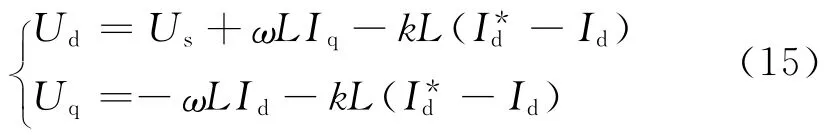
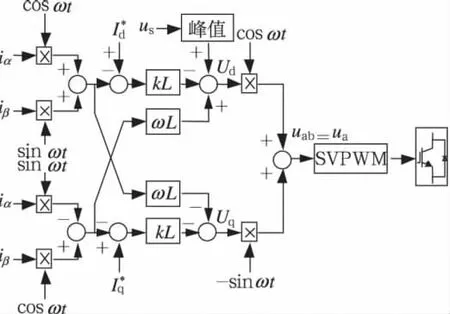
圖4 電流解耦控制框圖
由圖4可知,引入比例系數k后,電流內環中的PI調節器換成了比例調節器,一定程度上降低了控制系統的復雜度。此外,電網電壓幅值Us需作為前饋補償量用來消除網壓波動對系統的影響。
2.4 SVPWM 調制
根據調制信號um的大小可將單相三電平NPC整流器的9個工作模式劃分為如下4個工作區域:
(1)區域1:0.5<um/udc*≤1;
(2)區域2:0<um/udc*≤0.5;
(3)區域3:-0.5<um/udc*≤0;
(4)區域4:-1≤um/udc*≤-0.5。
其中udc*為直流參考電壓。
單相三電平NPC整流器9個工作狀態對應9個空間電壓矢量,其中3個零矢量VPP、VOO、VNN,4個小矢量VPO、VON、VNO、VOP,和2個大矢量VPN、VNP。矢量VXY中,X 表示SA的值(P、O、N),Y 表示SB的值(P、O、N)。圖5為SVPWM調制方式,調制信號um由幅值相差/2的兩個狀態量V1和V2的線性組合來合成[5]。在每個區域V2從大矢量或零矢量中選擇,而V1有兩個冗余狀態量V1+和V1-,且冗余狀態量只從小矢量中選擇[6]。
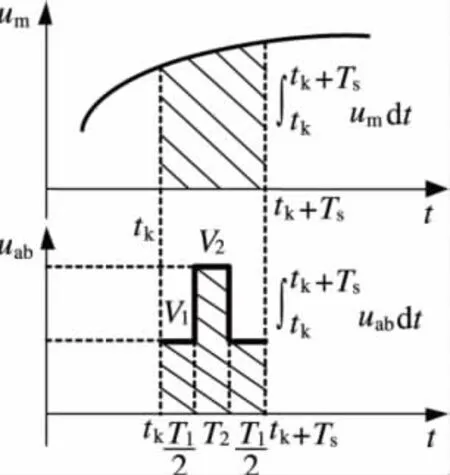
圖5 SVPWM調制
由圖5可以看出V1和V2滿足下式:

在一個開關周期Ts內,調制信號um可視為恒定值,利用伏秒平衡原理可得:
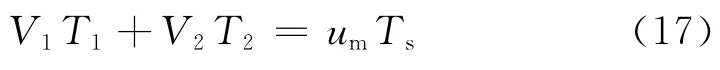
T1與T2分別為V1和V2的作用時間,且滿足:

聯立式(17)、(18)可得:

表1給出了4個工作區域中狀態量V1、V2與9個空間電壓矢量之間對應的矢量關系。

表1 狀態量與空間電壓矢量在4個工作區域中對應關系
為減小開關損耗和開關應力,文獻[7]提出優化的狀態量作用順序,分別為狀態量作用順序I:V1+→V2→V1-→V2→V1+和狀態量作用順序II:V1-→V2→V1+→V2→V1-,對應狀態量的作用時間分別為:T1+/2→T2/2→ T1-→T2/2→T1+/2 和 T1-/2→T2/2→T1+→T2/2→T1-/2。
3 仿真和實驗結果
為驗證電流解耦控制策略的可行性,采用PSIM進行計算機仿真,并進行了相應的樣機測試。系統參數如下:輸入電壓有效值實驗us= 50 V,Ls=4.3 mH,Rs=0.2Ω,開關頻率fs=2.5 kHz,直流參考電壓100 V,支撐電容C1=C2=3 300μF,負載功率200 W。
圖6為輸入電流無功分量參考值等于零時,1/2負載向滿載切換(1 s)前后的仿真波形,其中(a)為輸入電流有功無功分量幅值及其給定值波形;(b)為網側輸入電壓電流波形;(c)為輸出直流電壓。由圖6(a)可知,無論系統1/2負載還是滿載運行,輸入電流的有功、無功分量都能夠很好地跟蹤其給定值。由圖6(b)可知,網側輸入電流正弦度好,且能夠很好地跟蹤輸入電壓,功率因數接近1。由圖6(a)、6(c)可知,1 s投入負載后,大約經過0.3 s系統重新進入穩態,且輸入電流無功分量一直為零,系統動態性能良好。

圖6 1/2負載向滿載切換前后系統仿真波形
圖7為網側輸入電壓電流穩態仿真波形,其中(a)為輸入電流無功分量參考值=1時的波形;(b)為輸入電流無功分量參考值=-1時的波形。由圖7(a)可知,當輸入電流無功分量參考值=1時,網側輸入電流超前網側輸入電壓,此時整個PWM整流器相對于電網可以等效為一個容性負載,而當輸入電流無功分量參考值=-1時,PWM整流器相對于電網可以等效為一個感性負載。
試驗樣機與仿真參數一致,功率開關器件采用2MB175U4A-120絕緣柵雙極晶體管,驅動電路由具有短路保護功能的PC929搭建而成;采用TMS320F2812數字信號處理器完成系統的采樣和電平作用時間計算。

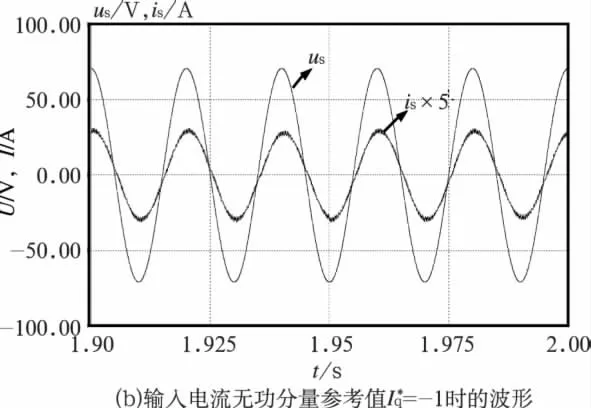
圖7 網側輸入電壓電流穩態仿真波形
圖8為整流工況下網側輸入電壓電流實驗波形。由圖8可知,輸入電流is能夠很好地跟蹤輸入電壓us,相位與其基本一致,功率因數較高。圖9為整流器輸入端電壓實驗波形。

圖8 網側輸入電壓電流波形

圖9 整流器輸入端電壓波形
4 結 論
本文基于dq坐標系推導了單相三電平NPC PWM整流器的數學模型,提出了電流解耦控制策略。該控制策略不僅實現d、q軸電流的解耦,而且比例控制器的使用大大降低了控制系統設計的復雜性。仿真和實驗結果表明:電流解耦控制策略能夠消除網側輸入電流的穩態誤差,實現網側高功率因數,并且具有很好的動態特性。
[1] 一種新的PWM整流器電流解耦控制策略[J].電工技術學報,2005,20(8):74-77.
[2] Miranda U A,Rolim L G B,Aredes M.A DQ Synchronous Reference Frame Current Control for Single-Phase Converters[C].Power Electronics Specialists Conference,PESC'2005.IEEE36th 2005:1377-1381.
[3] Salaet J,Alepuz S,Gilabert A,Bordonau J,Peracaula J.D-Q Modeling and Control of a Single Phase Voltage Balancing[C].IEEE Power Electronics Specialists Conference,2002,2:514-519.
[4] 顧 軍.基于電流解耦的雙閉環三電平PWM整流器研究[J].電力電子技術,2007,41(6):60-62.
[5] Salaet J,Gilabert A,Bordonau J,Alepuz S,Cano and Gimeno,Gimeno LM.Nonlinear Control Neutral Point in Three-level Single-phase Converter by Means of Switching Redundant States[C].Electronics Letters,2006.
[6] 馮曉云,宋文勝.單相三電平NPC整流器的SVPWM與中點電位控制方法[J].西南交通大學學報,2009,44(3):347-353.

