變槳轉盤軸承額定疲勞壽命計算
袁倩倩,王燕霜
(河南科技大學 機電工程學院,河南 洛陽 471003)
風力發電機變槳軸承普遍采用特大型雙排或者單排四點接觸球轉盤軸承,同時承受軸向載荷、徑向載荷及傾覆力矩。變槳軸承一般安裝在20多米的高空,更換和維修的成本較高[1]。因此風力發電機組的變槳軸承在設計選型過程中,需要利用可靠度方法計算其在一定可靠度下的壽命。
目前國內、外對單排四點接觸球軸承疲勞壽命的研究較多[2-5],而對多排四點接觸球軸承壽命的研究較少[6-7]。文獻[5]對比分析了各種計算軸承疲勞壽命的方法,并得出了應力-壽命法在某種程度上是計算滾動軸承疲勞壽命較為有效的方法。文獻[6]給出了一種三排圓柱滾子轉盤軸承在徑向、軸向載荷和傾覆力矩聯合作用下疲勞壽命的計算方法。文獻[7]給出了多排滾子轉盤軸承壽命估算的理論公式,但都沒有考慮游隙及所受載荷對軸承壽命的影響。
文中以某特大型雙排四點接觸球轉盤軸承為例,計算在聯合載荷作用下軸承的疲勞壽命。特大型雙排四點接觸球轉盤軸承在聯合載荷作用下的壽命計算關鍵在于對軸承內部載荷分布的計算;變槳軸承的速度一般較低,對軸承進行靜力學分析即能滿足要求。文中建立了變槳軸承的靜力學模型,用Newton-Raphson迭代法對其進行求解,并根據Hertz接觸理論求得軸承內部載荷分布,在此基礎上計算出套圈當量滾動體載荷,結合套圈的額定滾動體載荷計算出整套軸承的壽命;最后分析了軸承的游隙與溝曲率半徑對其壽命的影響。
1 變槳軸承載荷分布
靜力學分析時,假設軸承外圈固定,外力(軸向力Fa、徑向力Fr及傾覆力矩M)作用在內圈上。軸承為四點接觸,這里將軸承承受主要軸向力的接觸對稱為接觸對1(上排)、接觸對3(下排),對應的另外兩個接觸對分別稱為接觸對2(上排)、接觸對4(下排),如圖1所示。圖中,Dpw為軸承球組節圓直徑,dc為兩排鋼球之間的中心距。
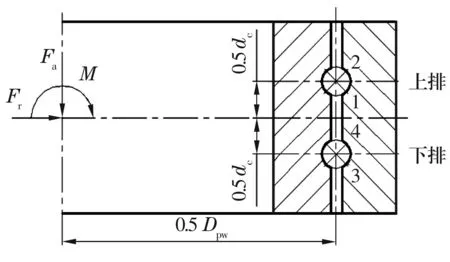
圖1 軸承受力圖
軸承受載前,任意鋼球位置接觸對的內、外圈溝曲率中心距為
(1)
式中 :fi為內溝曲率半徑系數;Dw為鋼球直徑;fe為外溝曲率半徑系數;Ga為軸承的軸向游隙;α0為軸承未受載前的接觸角。
軸承受載前,當鋼球與溝道間的游隙為0時,任意鋼球位置接觸對的內、外圈溝曲率中心距為
A0=(fi+fe-1)Dw。
(2)
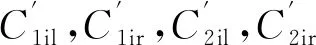
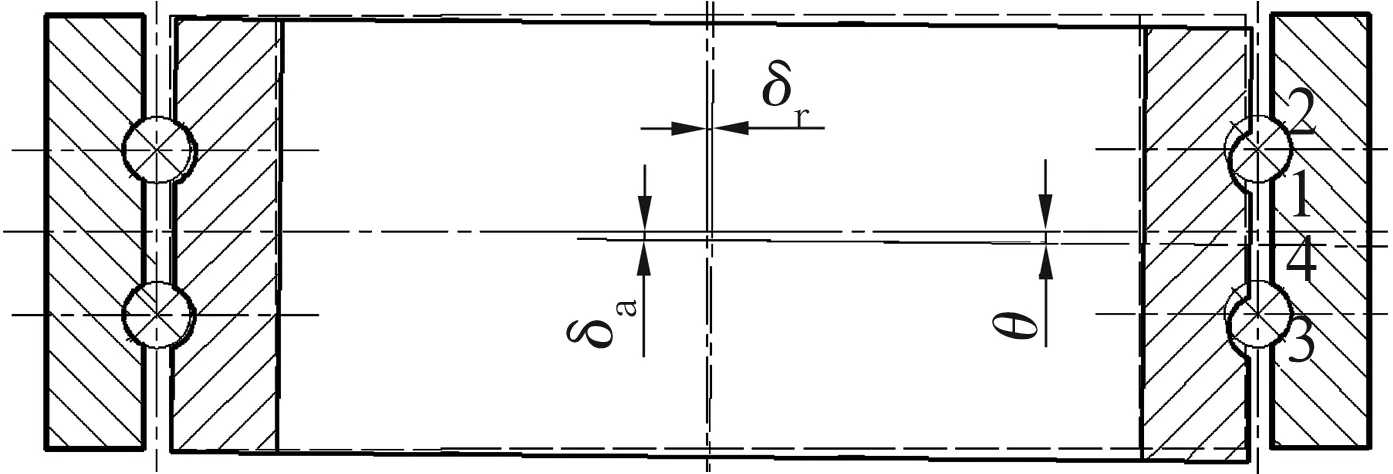
圖2 聯合載荷作用下內外圈相對位移
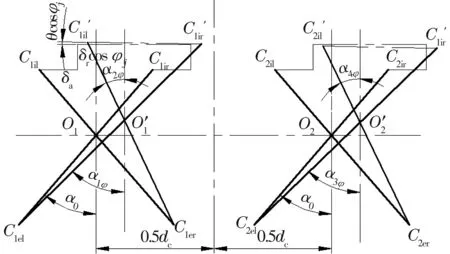
圖3 任意位置鋼球球心與內、外溝道曲率中心的最初和最終位置
A1φ=[(Asinα0+δa+Riθcosφ)2+(Acosα0+

(3)
A2φ=[(Asinα0-δa-Riθcosφ)2+(Acosα0+

(4)
A3φ=[(Asinα0+δa+Riθcosφ)2+(Acosα0+
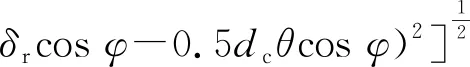
(5)
A4φ=[(Asinα0-δa-Riθcosφ)2+(Acosα0+
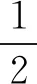
(6)
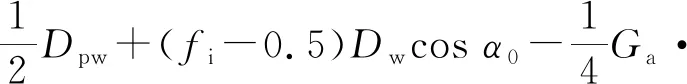
(cosα0)2,
(7)
式中:Ri為內圈溝曲率中心圓半徑;φ為鋼球的位置角,φk=2π(k-1)/(Z/2),Z為軸承鋼球總數(k=1,2,3,…,Z/2)。
在接觸對j的位置角φ處,鋼球與溝道總的彈性接觸變形量δjφ為
δjφ=Ajφ-A0。
(8)
內圈發生位移后,接觸對j在位置角φ處的接觸角αjφ分別為
(9)
(10)
(11)
(12)
根據Hertz點接觸理論,接觸對j在位置角φ處法向接觸載荷Qjφ和接觸變形δjφ的關系為[2]
(13)
式中 :Kn為鋼球與內、外圈總的載荷變形常數,由軸承的材料和幾何參數確定[8]。
在角位置φk處,內圈受到軸向載荷、徑向載荷、傾覆力矩以及鋼球對內溝道的接觸載荷的作用,如圖4所示。
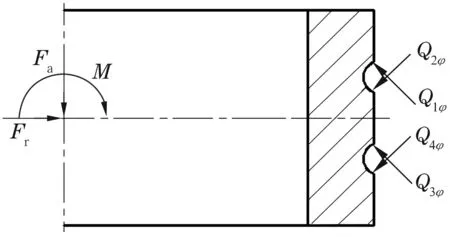
圖4 作用在內圈上的力
內圈在外部載荷和所有鋼球接觸載荷的作用下處于平衡狀態,內圈的力學平衡方程為
Q4φsinα4φ)-Fa=0
(14)
Q4φcosα4φ)cosφ-Fr=0
(15)
Q2φcosα2φ-Q3φcosα3φ-Q4φcosα4φ)cosφ-M=0。
(16)
(14)~(16)式構成的方程組是δa,δr和θ為未知量的三元非線性方程組。求解該方程組可以獲得鋼球接觸載荷分布Qjφ。
2 基于載荷分布的軸承壽命計算
根據Lundberg-Palmgren理論,在進行變槳軸承額定壽命的計算時,先分別計算各個溝道的壽命,然后計算單個套圈的額定壽命,最后擬合出整個軸承的額定壽命。普通軸承中球與內、外溝道接觸時一般為2點接觸,由于這里所討論的軸承溝道為桃形溝道,如圖5所示,一個鋼球與內、外套圈接觸時為4點接觸。則單個套圈的額定壽命為與鋼球接觸的兩個溝道的擬合值,把接觸對1,2,3,4上的溝道分別命名為溝道1,2,3,4。
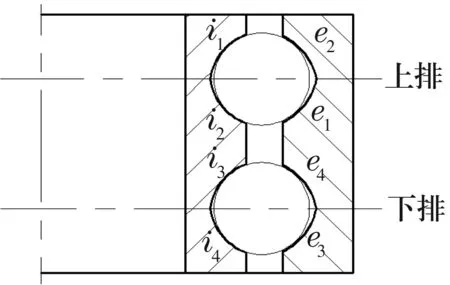
圖5 雙排四點接觸球轉盤軸承溝道結構簡圖
對于四點接觸球軸承,套圈的額定動載荷為
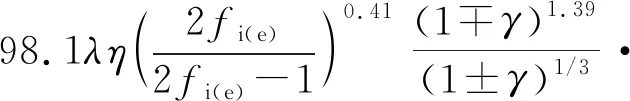
(17)
式中:上面的符號適用于內圈,下面的符號適用于外圈;λ,η分別為球軸承的修正系數,取值可查文獻[9]得到。
由于外圈固定,內圈旋轉,內圈溝道j上的當量滾動體載荷為
(18)
式中:Qjφ為鋼球接觸載荷,N。
內圈上各溝道的額定壽命為
L10ij=(Qcij/Qeμj)3。
(19)
內圈額定壽命為
(20)
外圈上溝道j的當量滾動體載荷為
(21)
則外圈上各溝道的額定壽命為
L10ej=(Qcej/Qevj)3。
(22)
外圈額定壽命為
(23)
則變槳軸承的額定壽命為
(24)
變槳軸承的額定壽命用工作小時數表示為
L10h=106L10/(60ni),
(25)
式中:ni為軸承內圈轉速。
3 計算實例及結果分析
以某型號雙排四點接觸球轉盤軸承為例進行疲勞壽命計算,其結構參數為:球組節圓直徑Dpw=2 215 mm,鋼球直徑Dw=44.45 mm,初始接觸角α0=45°,兩排鋼球之間的中心距dc=69 mm,內、外圈溝曲率半徑系數fi=fe=0.525,鋼球總數Z=256。鋼球與套圈均采用42CrMo鋼,泊松比ν=0.3,彈性模量E=207 GPa。當軸承轉速ni=0.1 r/min,軸向載荷Fa=250 kN,徑向載荷Fr=140 kN,傾覆力矩M=1 300 kN·m時,計算其疲勞壽命,取軸承游隙為0,-0.01,-0.02,-0.03,-0.04,-0.05,-0.06及-0.1 mm,將以上參數代入(14)~(16)式,利用Newton-Raphson迭代法計算出δa,δr和θ,并根據(13)式計算出軸承在不同位置角處的法向接觸載荷。將所求結果及參數代入(17)~(25)式,計算軸承套圈及整套軸承的額定壽命,結果見表1。由表中可以看出,隨著軸承負游隙絕對值的增大,變槳軸承額定壽命先增大后減小。變槳軸承一般要求20年的使用壽命[10],相當于175 200 h,當軸承游隙為-0.04~0 mm時可以滿足要求。因此,在設計變槳軸承時為了滿足軸承壽命的要求,應選擇合理的軸承游隙。
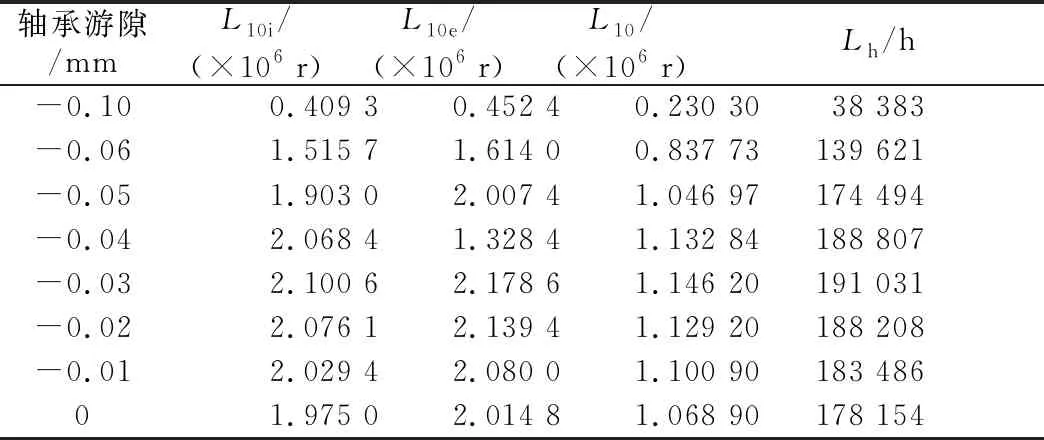
表1 不同游隙下的計算結果
當軸承游隙為0,取不同的軸承溝曲率半徑時,套圈及整個軸承的額定壽命的計算結果見表2。由表2可以看出,變槳軸承溝曲率半徑系數越大,軸承的壽命越小。這主要是因為隨著溝曲率半徑系數增大,鋼球與溝道的密合度減小,在同樣的載荷作用下其接觸橢圓面積就相對較小,接觸應力較大,從而降低了軸承壽命。
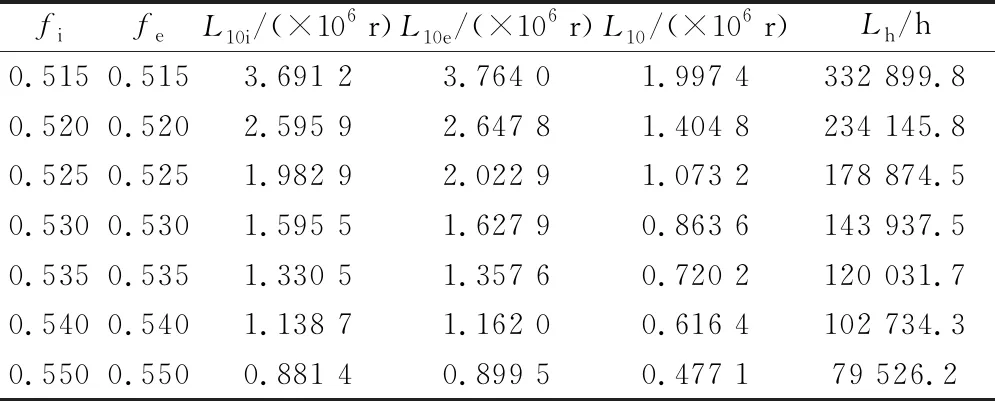
表2 當游隙為0時不同溝曲率半徑系數下的計算結果
4 結論
變槳軸承隨著負游隙絕對值的增大,額定壽命先增大后減小。變槳軸承在承受聯合載荷時,可采用文中的計算方法計算疲勞壽命,選取合理的軸承游隙。在其他結構參數確定的情況下,軸承溝曲率半徑系數越大,軸承的額定壽命越小。

