水平常幅荷載作用下塑性鉸滯回衰變特征對RC框架結構屈服力的影響
王飛婭,張 偉,余立軍
(1.廣州城建職業學院建筑工程管理系,廣東廣州510925;2.湖南百利工程科技有限公司,湖南益陽414000;3.安徽省交通勘察設計院廣州分院,廣東廣州510620)
在地震發生的過程中結構經歷顯著的彈塑性變形。在結構性能沒有損傷之前,結構的強度、剛度和穩定性受最大響應位移控制。在結構開始損傷后,反復的非彈性位移循環會導致結構的強度和剛度降低,也就是結構的性能降低[1]。由于將框架結構塑性發展區域集中在塑性鉸部位,因此各塑性鉸性能的退化決定了結構抗側剛度的退化,進而決定了結構構件的屈服力的退化。
1 基于能量的恢復力模型
利用17根鋼筋混凝土梁進行了17組不同的實驗[2]。該試驗還通過歸一化處理試驗數據后,得到一條在常幅荷載作用下的名義耗散周期曲線,并用一個能代表這條平均曲線的指數函數來分析構件能量耗散的形式,如圖1。
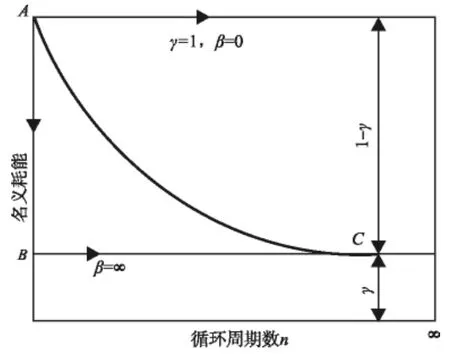
圖1 含γ,β兩個參數的耗能示意
這條平均曲線所代表的指數函數為:
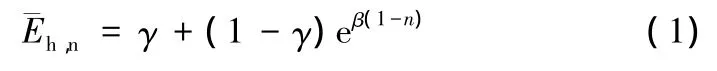
公式中:珔Eh,n是在周期為n的名義耗能;1-γ是能耗能力;β代表損傷速度。
當n=1時:
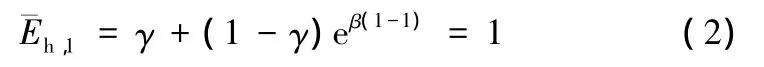
表示在第一個周期內的名義能耗恒為1.0。
當n→∞時:

表示構件不會在隨荷載的低周往復作用而耗散能量。
珔Eh,n的函數式包括n,γ,β三個參數。由圖1可以看出隨著循環次數n的增加,珔Eh,n的值都是隨循環周期數n的增加而減小的。圖1對γ,β的限制情況進行了說明。γ=0表示耗散所有的能量,當n趨于無窮大時,γ=1表示不耗散任何能量。因此,γ=0表示一個在剛度和強度中的嚴重的耗散系統,γ=1表示理想彈塑性非耗散的滯回系統。第二個參數β在0和無窮大之間變化,它表示在周期能耗能力的速率。在極限情況下,β=0是一個沒有耗散的理想系統,它表示在完成第一個周期后損失所有的能量。珔Eh,n的值在(γ,1)這個區間范圍內,當n無窮大時珔Eh,n的值不在減小為γ,β的取值,影響珔Eh,n的值從1衰減到γ的速度快慢。由圖1可以看出當β=0時珔Eh,n的值在n=1(即第一個周期)時就耗散了所有的能量。β=∞時珔Eh,n的值衰減的速度最慢,其衰減路徑ABC。圖1中曲線AC為β取(0,∞)之間的值時的衰減路線,近似為指數曲線。則γ決定珔Eh,n的衰減值和衰減剩余值,β決定珔Eh,n的衰減速度。最終珔Eh,n的值隨著循環次數n的增大而減小。
2 恢復力模型的定量描述
該實驗還確定了一個強度退化的雙線型恢復力模型。模型為一個強度退化的雙線型恢復力模型,并可預測等幅荷載位移循環下的能源耗散。其滯回環包圍面積表示在一個循環下,該構件的滯回耗能量(圖2)。
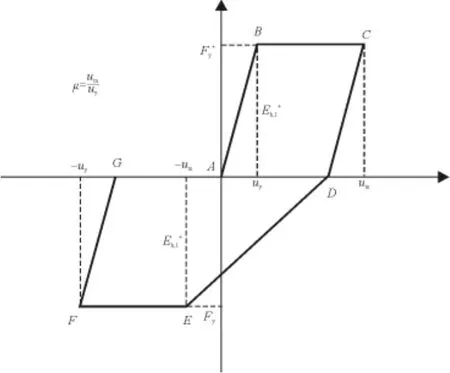
圖2 試驗中提出的基于能量的低周疲勞模型
圖2表示當n=1時,鋼筋混凝土構件的第一個滯回環。由圖2中的幾何關系可以看出:
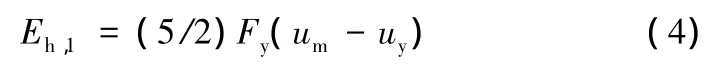
式中:Fy為構件的屈服力;um為構件的最大彈塑性位移;uy為構件的屈服位移;Eh,1為構件經歷第一次荷載循環后的滯回耗能量。
假定位移最大值um保持不變,則每次使構件達到相同最大位移的能量隨著荷載循環次數n的增大而減小。因為在滯回曲線中滯回環的面積代表了構件耗散的能量,則在荷載循環加載一次到達um的值后,滯回環所包圍的面積也減少。由基于能量提出的這個滯回曲線的特性可以定性地描述該構件經歷常幅荷載加載n個循環周期的滯回曲線。即恢復力模型,見圖3。
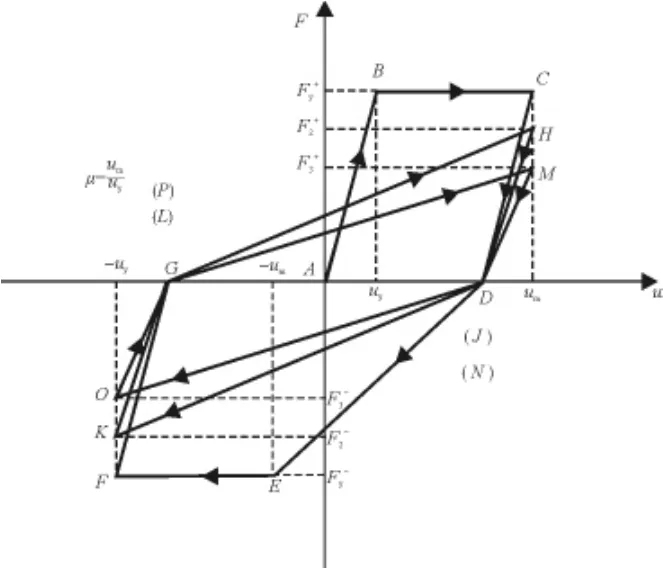
圖3 理想的雙線型非彈性體系恢復力模型
以3個循環周期為例,從圖3可以看出:
當循環周期n=1時,周期路徑為ABCDEFG;n=2時,周期路徑為GHJKL;n=3時,周期路徑為LMNOP。
在恢復力模型中每一個循環中作用力和位移與循環周期的對應關系見表1。
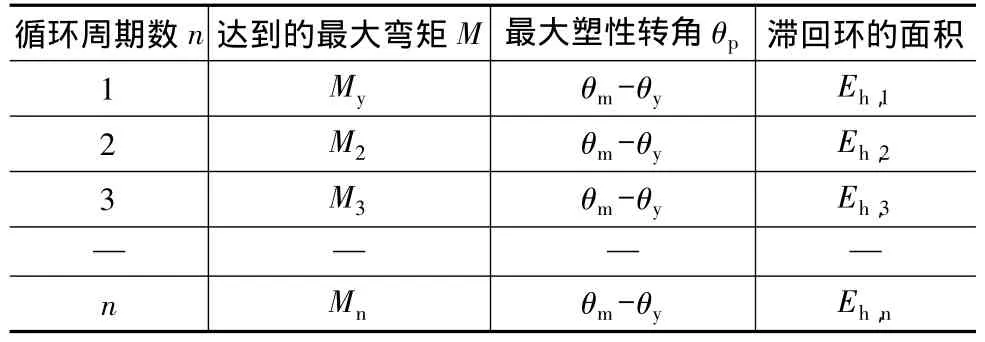
表1 恢復力模型中每一個循環中作用力和位移與循環周期的對應關系
從圖3中的幾何關系可以看出:
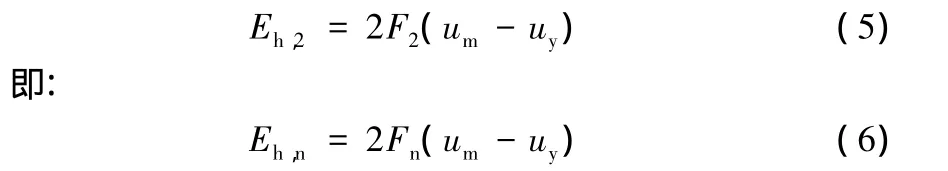
又由比例關系有:
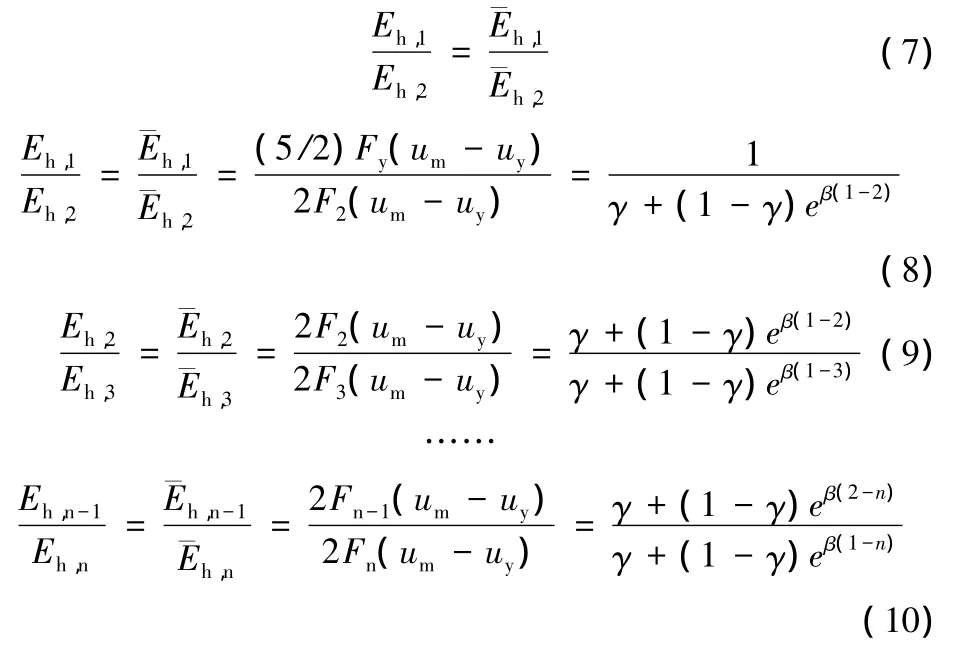
聯立式(8),式(9),式(10)則可推出:
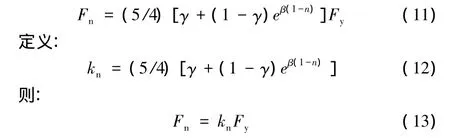
由上式可求出圖4中對應的F2,F3,F4,…,Fn的值。在定性描述的基礎上定量的描述了此恢復力模型。確定了塑性鉸滯回衰變特征對RC框架結構構件屈服力的影響。
3 總結
一般而言,對結構施加外力,結構會有相應的反力產生。如果結構產生的反力足以抵抗外力對結構的作用則結構處于彈性變形。如果外力作用超過了結構的承載能力結構就會被破壞,結構處于彈塑性變形。
鋼筋混凝土結構累積損傷破壞的特點是結構位移沒有超過某一限值,但位移往復次數的增加仍導致結構破壞,這表明隨著損傷的加劇,結構發生倒塌的位移限值是一個不斷變小的量。結構的倒塌源于二階效應不穩定,而該穩定性可以通過結構剛重比進行控制,所以結構位移限值的變化取決于剛重比值的變化,即結構抗側剛度的變化。由于將框架結構塑性發展區域集中在塑性鉸部位,因此各塑性鉸性能的退化決定了結構抗側剛度的退化,進而決定了結構構件的屈服力的退化。
[1]劉哲鋒,沈蒲生,胡習兵.地震總輸入能量與瞬時輸入能量譜的研究[J].地震工程與工程振動,2006,26(6):31-36
[2]Altug Erberik,Haluk Sucuoglu.Seismic energy dissipation in deterioratingsystemsthroughlow-cyclefatigue[J].Earthquake Engineering and Structural Dynamics,2004,33:49-67

