船橋撞擊力規范公式的合理性研究
熊安平,程海根,岳 振
(1.華東交通大學土建學院,江西南昌330013;2.江蘇盛華工程監理咨詢有限公司,江蘇徐州221011)
對船橋撞擊過程的研究中,現有規范應該包括幾個方面的考慮:設計思路、設計策略、設計撞擊力[1]。其中設計撞擊力又是尤為重要的,然而對設計船撞力取值問題還存在著爭議,主要包括了下面兩個問題:一是如何獲取船舶撞擊力的精確時程,另外一個問題是將動態的撞擊力轉化為一個現有規范闡述的靜態力的合理性。到目前為止,船撞力時程只有通過有限元軟件仿真計算來獲得。
1 橋梁船撞力常用的規范公式及合理性內容
1.1 AASHO 規范公式[2]
美國聯邦公路與運輸協會指導規范對于船舶碰撞荷載提出了經驗公式,其船舶碰撞荷載是對于設定的碰撞條件下考慮水域特征,不同的交通流量,橋梁的重要程度(關鍵或者一般)這些因素下進行計算的。AASHO規范公式用下面的公式估算船舶與剛性橋墩正面碰撞的靜力碰撞荷載Ps:
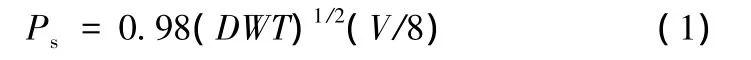
式中:Ps為船舶碰撞荷載等效靜力荷載(MN);DWT為輪船噸位;V為船舶碰撞速度(m/s)。
1.2 歐洲規范公式[3]
1999年歐洲統一規范在橋梁的船撞設計中,選用某種統計意義下的設計代表船舶,并按照下式來計算船舶的撞擊力:

式中:V為碰撞體在撞擊時的速度(m/s);K為碰撞體的等效剛度;M為碰撞體的質量。
參數取值在規范中如下規定:對于內陸航道船舶,K=5 MN/m;對于遠洋船舶,K=15 MN/m。應該注意的是K表示的是碰撞體的剛度。
1.3 我國《鐵路橋涵設計基本規范》公式[4]
在《鐵路橋涵設計基本規范》中,將船舶對墩臺的撞擊力列入特殊荷載的計算中,其計算方法采用靜力法且基于能量理論推導的,可用下面的公式來表示:
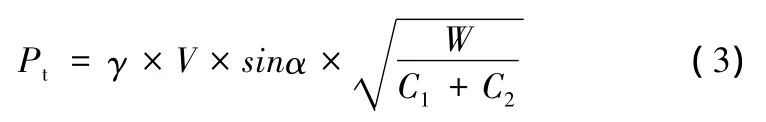
式中:Pt為船舶撞擊力(MN);V為船舶撞擊墩臺的速度(m/s);W為船舶的重量(MN);C1,C2為船舶的彈性變形系數和墩臺圬工的彈性變形系數(m/MN),當無實測資料時,可取C1+C2=0.5;α為船只駛近方向與墩臺撞擊點處切線所成的夾角。如有困難可取20°;γ為動能折減系數,當船只斜向撞擊承臺時取0.2,正向撞擊時,可采用0.3。
1.4 規范的合理性研究的內容
規范公式合理性研究無非是從設計思路、設計策略、設計撞擊力來考慮。歐、美規范在細節上稍微有所差別,但是設計思想和設計策略基本上相同,都是把船撞橋處理為風險事件。然而中國規范只是將船橋撞擊力處理為偶然荷載,并且設計思路和設計策略不明確,這些顯然是不合理的。
對于設計撞擊力是否合理則是通過其計算出來的橋梁靜態荷載作用下內力、位移和動態撞擊力計算出來的內力、位移反應的幅值是否能夠基本上一致。動態力計算出來的內力、位移幅值與規范公式等效靜力計算出來的內力、位移將會受到撞擊力大小的影響即船舶和速度等。因此就要根據速度和質量分若干工況,在不同規范公式下對不同工況進行仿真分析,這樣就會非常繁瑣和復雜。所以有必要引入一個靜態撞擊力等于動態撞擊力幅值的公式和其他規范公式進行比較得出中國和歐美規范的合理性,這樣可以簡化整個分析過程。
2 引入新的撞擊力公式并對各公式所得撞擊力進行比較
2.1 新的撞擊力公式
引入撞擊力公式[5]是運用有限元軟件仿真分析,通過數理統計擬合出來。其適用范圍更大,還包括了撞擊角度以及承臺因素的考慮。公式如下:其中 γ1=K cosα+γ0;K=a0/DWTb0;a0=51.57;b0=0.48;γ0=1-K。
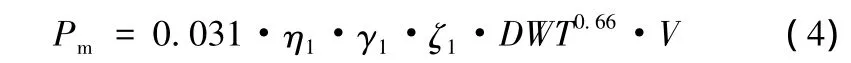
式中:Pm為最大撞擊力(MN);DWT為船舶的裝載噸位或滿載排水量(t);V為船舶撞擊速度(m/s);η1為最大撞擊力承臺厚度修正系數;γ1為最大撞擊力碰撞角度修正系數;ζ1為最大撞擊力承臺圓弧半徑修正系數。
引入公式在本文分析中并沒有考慮承臺因素對撞擊力的影響,故只列出γ取值公式,對于η、ζ則為1。
2.2 撞擊力公式的比較
下面將對上述四個撞擊力公式進行對比分析,如圖1~圖4給出了各種載重噸位船舶正面撞擊橋梁的等效撞擊力隨速度變化的關系。從圖中可以看出,各種噸位船舶的等效撞擊荷載隨速度成線性變化,其中Pe1為內陸船舶的歐洲規范撞擊力,Pe2為遠洋船舶的歐洲規范撞擊力。并且無論船舶的噸位和速度如何的變化,規范公式中遠洋船舶的歐洲規范撞擊力是最大的,緊接著AASHO規范撞擊力、內陸船舶的歐洲規范撞擊力、我國《鐵路橋涵設計基本規范》公式撞擊力。當噸位增加時,四個公式撞擊力也隨之增加,然而新引入公式撞擊力隨噸位增加的幅度會比其他規范公式都要快,當船舶噸位等于5 000 t時,Pm與Ps幾乎相等,當噸位達到12 000 t時,Pm與Pe2幾乎相等,大于12 000 t時,Pm成為最大撞擊力,然而Pe1、Pt在任何情況下都是小于Pm。
隨著速度的增加,四個公式的撞擊力也隨之相差越大。圖5給出了DWT=3 000 t船舶在4 m/s的情況下斜撞橋梁的等效撞擊力隨撞擊角度變化的關系。從圖中可以看出,引入撞擊力公式對角度變化的影響比我國《鐵路橋涵設計基本規范》公式撞擊力更加敏感,但是Pm始終大于Pt。
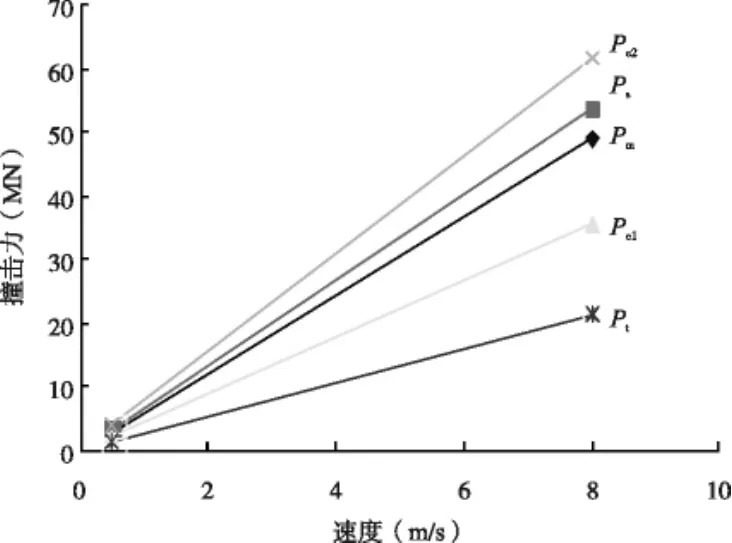
圖1 DWT∶3000(M ∶3962)船的撞擊力
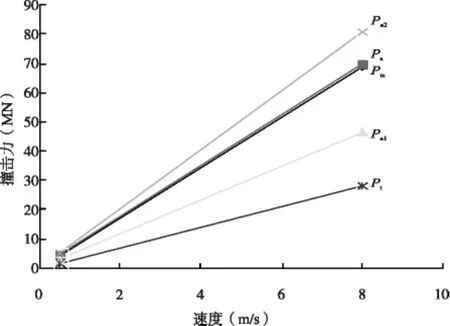
圖2 DWT∶5000(M ∶6710)船的撞擊力
3 船橋撞擊動力響應分析
3.1 動力放大系數影響因素的考慮
船舶與橋梁的撞擊時間只有3~5 s,阻尼對動力放大系數的影響可以不考慮,所以只需考慮結構物的固有頻率和撞擊時間這兩個因素。船舶質量和速度會對撞擊力造成非常大的影響,但是荷載的大小對動力放大系數是沒有影響的,因此船舶的質量和速度并不會直接影響動力放大系數,但是其會影響撞擊時間間接影響到動力放大系數,這些還有待研究。所以船舶質量和速度、外界因素、船舶內部構造細節對動力放大系數的影響不予考慮。
對于斜撞的問題,可以將撞擊力沿順橋和橫橋向進行分解得出的兩個方向的動力放大系數差別是非常微小的[6],且分解出來的撞擊力的撞擊時間也是相等的,因此斜撞對動力放大系數的影響非常小,表1~表3中剛構橋的正撞和斜撞的動力放大系數可以說明這一結論。
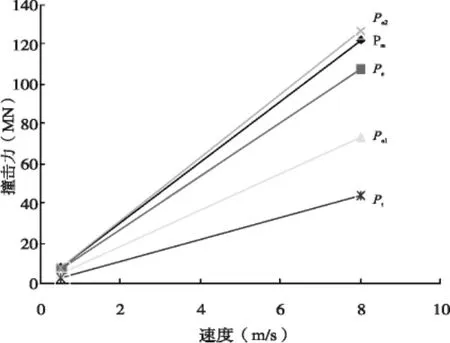
圖3 DWT∶12000(M ∶16700)船的撞擊力
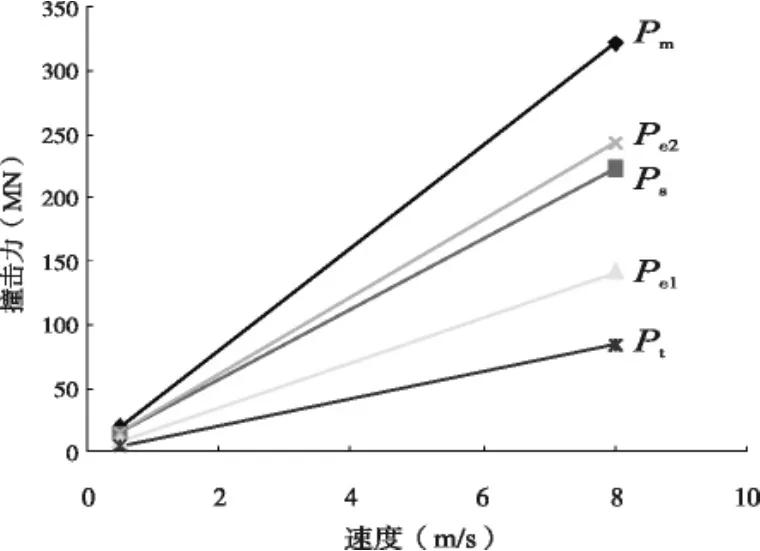
圖4 DWT∶52300(M ∶62000)船的撞擊力
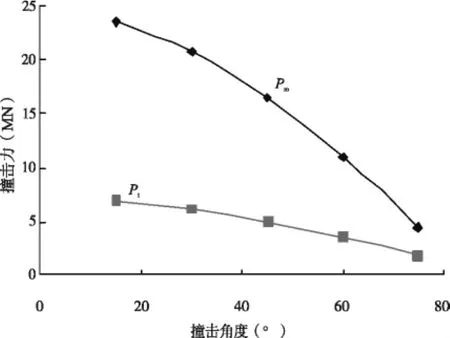
圖5 DWT∶3000(M ∶3962)船的撞擊力
3.2 有限元仿真結果分析
以下是對連續剛構橋、斜拉橋和連續梁橋在不同工況下仿真計算結果[5]的分析。從表1~表3可以看出,在墩頂和樁頂這兩個重要部分,除了5 000 DWT斜撞斜拉橋主塔墩外,在其他工況下動力放大系數都非常接近1。而不同工況對動力放大系數沒有影響,所以表中的動力放大系數在某一特定橋型下具有一般性。
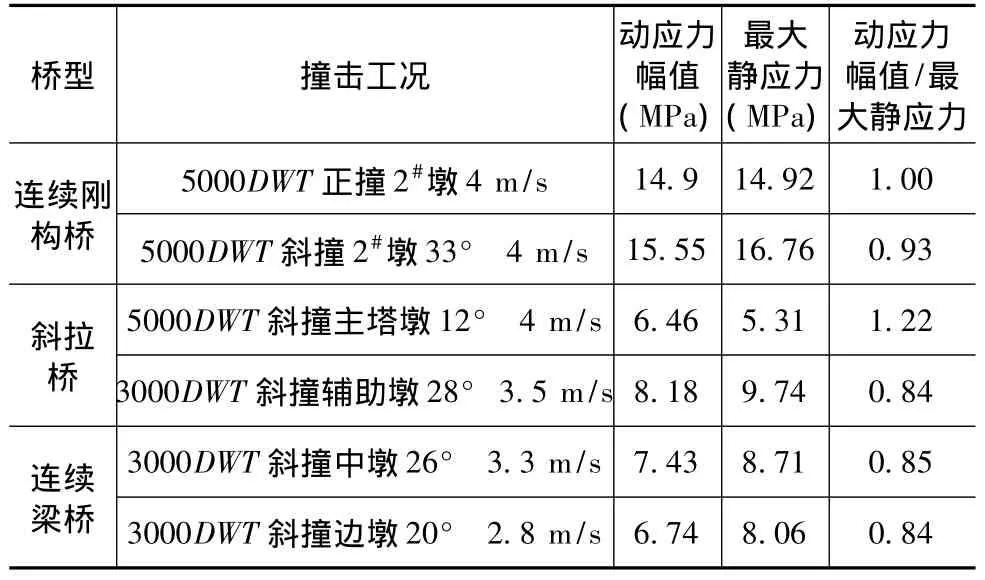
表1 各工況下樁頂動應力與最大靜應力的比較
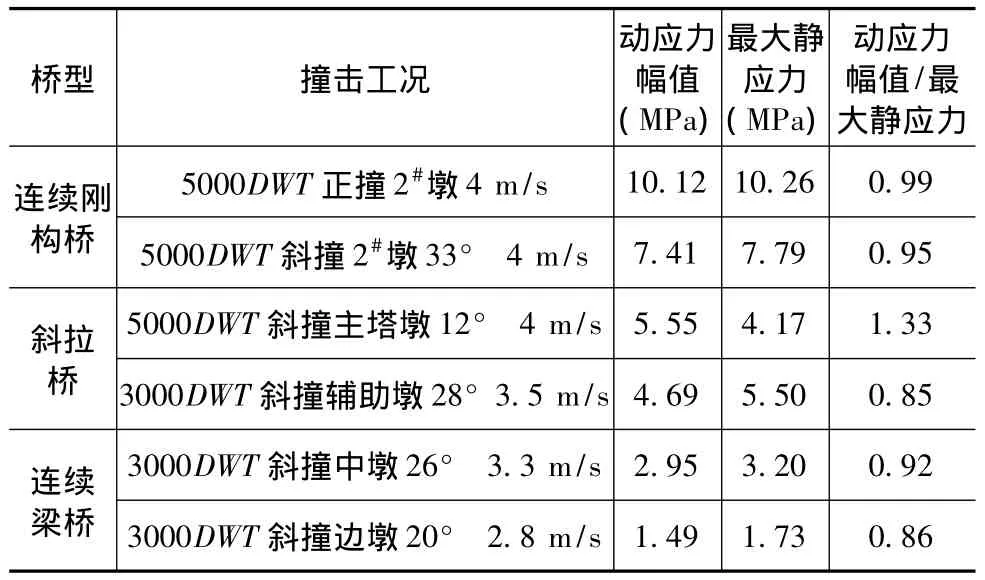
表2 各工況下樁頂橫橋向動應力與最大靜應力的比較
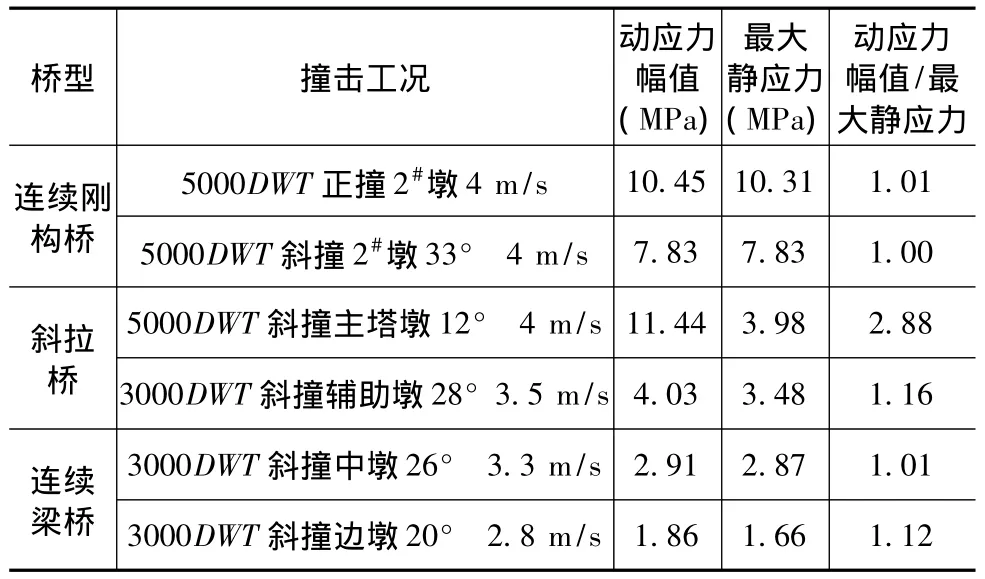
表3 各工況下墩頂橫橋向動應力與最大靜應力的比較
動力荷載計算內力和位移幅值Pm計算出來的內力和位移=動力放大系數,當動力放大系數等于1時只要規范公式計算出來的撞擊力 Ps、Pe1、Pe2、Pt能夠等于 Pm則說明規范公式是合理的,所以影響規范撞擊力與Pm差值的因素都將影響規范公式的合理性即船舶重量、速度和撞擊角度。從上等式可以看出,動力放大系數對規范公式合理性也是有影響的,在此不考慮船舶本身和外界因素對動力放大系數的影響即只有結構物的剛度和重量、撞擊時間。動力放大系數與固有頻率成正比,而結構固有頻率與結構剛度成正比、與重量成反比,所以動力放大系數與結構剛度成正比、與重量成反比。
綜合上述可以總結出,規范公式合理性與船舶的速度、船舶重量、結構物的重量成反比,與撞擊角度、撞擊時間、結構物的剛度成正比。對于上述特定橋型下分析中即結構物剛度和重量一定,其動力放大系數大致等于1,影響合理性的因素只有船舶的速度、剛度和撞擊角度。當船舶噸位等于 3 000 t、5 000 t時,Ps、Pe2都大于 Pm,AASHO 規范和遠洋船舶下的歐洲規范是合理的。當噸位達到12 000 t時,Pm與Pe2幾乎相等,遠洋船舶下的歐洲規范是合理的。當噸位大于12 000 t時,所有規范公式都是不合理的。而當噸位大于3 000 t時,內陸船舶下的歐洲規范和我國《鐵路橋涵設計基本規范》公式都是不合理的,因此速度和撞擊角度不會對合理性起到本質的改變,只是會影響到其合理性的一個趨勢。
4 結論
判定某個規范公式是否合理要根據船舶的速度、重量、撞擊角度和橋梁的剛度、重量、撞擊時間的情況而定,但是總的來說歐美規范要比我國《鐵路橋涵設計基本規范》公式趨于合理。我國《鐵路橋涵設計基本規范》公式在動力放大系數、船舶速度、船舶重量都非常小的情況下,才是趨于合理的,所以適用范圍比較小。
[1]項海帆,范立礎,王君杰.船撞橋設計理論的現狀與需進一步研究的問題[J].同濟大學學報,2002(4):386-392
[2]AASHTO 1991.Guide Specificationsand Commentary for Vessel Collision Design of Highway Bridges.American Association of State High and Transportation Official,Washington D.C.
[3]A.C.W.M.Vrouwenvelder.Design for Ship Impact According to Eurocode 1,part 2.7,Ship Collision Analysis.A.A.Balkema,Rotterdam,1998
[4]TB 100021-99鐵路橋涵設計基本規范[S]
[5]陳誠.橋梁設計船撞力及損傷狀態仿真研究[D].上海:同濟大學,2006
[6]廖小軍.船舶側向撞擊橋梁基礎的動力放大系數探討[J].公路交通技術,2009(3):78-83

