鋼鐵企業廠內運輸方式經濟性模糊分析

楊秋俠，左精力

(西安建筑科技大學土木學院，陜西西安710055)

鋼鐵企業往往是擁有多個生產單元的綜合體，生產規模大，運輸復雜，涉及的運輸方式趨于多樣化。有數據顯示聯合鋼鐵廠的經濟規模在850×104t以上[1]，而現代化的鋼鐵聯合企業生產規模達1 000×104t以上。按照廠內噸鋼運輸比4.5計算[2]，企業內部運輸量將達到 4 500×104t，再按照年運營成本汽車0.6元/(t·km)、鐵路0.15元/(t·km)、皮帶0.05元/(t·km)，三種運輸方式平分總量，則廠內物流的年運營成本分別為道路900×104元/km、鐵路225×104元/km、皮帶75×104元/km。廠內運輸距離一般在數千米左右，可以看出不同的運輸方式年運營成本可達數千萬的差異，因此對鋼鐵企業運輸方式選擇的進一步研究顯得十分必要。

對于廠內運輸方式的選擇，需要在總圖初步設計時予以考慮，傳統的方法是根據設計規模、工藝、總平面、可行性、經濟性等方面綜合考慮。對于經濟性分析，一般只計算建設總成本和年運輸費用，而缺少進一步的數據分析，也沒有分析計算誤差大小。因此可以針對鋼鐵企業廠內運輸，分析成本組成和其選擇特點，建立帶有時間和偏差因素的經濟性分析模型，進行多方案的模糊比選。

1 鋼鐵企業廠內運輸方式構成及特點

廠內運輸指廠區范圍以內的運輸，還包括由企業建設運營的廠外部分[3]。鋼鐵企業廠內經常采用的運輸方式有鐵路、汽車、帶式、管道等。不同的運輸方式有不同的構成，且同種運輸方式會因具體條件的不同可能存在較大的差異，下邊分析其構成和特點。

1.1 鐵路運輸

鋼鐵企業廠內鐵路可以分為運入運出線、鐵水線、碼頭線、渣線等，這些子系統各自內部的運輸頻繁，相互之間的運輸較少。主要作為大量運輸的手段，當運量和運距較小時不經濟。鐵路系統固定成本包括土石方量、鐵路站場、線路、車輛、裝卸設備、附屬設備，運營成本可參照當地鐵路貨運單位運輸成本。其土石方量因方案不同而不同，差異比較大且存在較大的誤差;鐵路站場和運輸量、種類有關;線路指鋪軌長度，還區分窄軌、標準軌、線路等級等;車輛數量與運輸量、生產工藝相關。

1.2 道路運輸

廠內道路分為主干道、次干道、輔助道路、車間引道、人行道，其中主干道和次干道為車輛通行道路，一般廠內采用城市道路類型，廠外采用公路型。道路的設置以保證生產運輸為前提，根據重要程度確定寬度，根據荷載確定路面結構，根據運量和貨物確定車輛類型、裝卸設備等。在廠內運輸中幾乎所有的物品都可以用道路來運輸，是最為靈活的運輸方式。道路系統的固定成本包括道路路基、路面、車輛、裝卸設備、附屬設施，運營成本可參照當地單位運輸成本。

1.3 帶式運輸

帶式運輸是廠內運輸的重要組成部分，一般用于散狀物料的輸送，是連續生產的重要保障。其線路靈活，長度從幾米到幾十千米以上均可實現，也可以架設在地面交通混亂和危險地區的上空，但是在轉彎時需要設置轉運站。輸送能力一般為200～8000 t/h，形式多樣，現在越來越多的設計采用圓筒式皮帶運輸。帶式運輸系統的固定成本包括建筑安裝、設備(皮帶、轉運站)、工程建設，運營成本包括工資、動力、備品備件折算，也可折算成單位運輸成本。

1.4 管道運輸

管道運輸是廠內運輸網中重要組成部分，一般用于輸送液體和氣體，也可以將固體轉化為固液混合狀態，或通過氣動管輸送粉體或小顆粒固體。在鋼鐵廠內，管道運輸很大一部分都是工藝管，一般架設在地面管架上，只有很少一部可以被其他運輸方式取代。其速度和流量根據壓力和管徑，差距比較大。管道運輸系統的固定成本包括安裝、管材(規格和長度)、其他設備，運營費用包括人工、能源消耗、管理維護等，也可折算成單位運輸成本。

1.5 其他運輸

鋼鐵企業生產還包括其他運輸方式，如輥道、索道、鏈條、特種運輸等。其費用的估算和上邊主要運輸方式的估算方法類似。

2 問題分析

通過上邊的分析，發現成本由建設和運營兩部分組成，建設成本是一次性的投入，而運營成本是分每年的投入，需要計算多年的累積就必須考慮資金的折算問題;另外大部分數據是估算或者參考同類設計的結果，是帶有偏差的，如果每一個小項都有偏差，就會形成累積偏差，這個偏差到底是多大，對比選結果影響怎樣分析，成為討論的重點。

對于帶有時間和偏差的多種運輸方式經濟性比選，可以看成是多個數值取小的模糊選擇問題，具體做法如下。首先，確定備選的運輸形式和基本組成，以估算各項的投資數目和對應的偏差量。對于每一項具體內容，往往存在多種選擇，且費用是變化的，但大部分都有一定的變化范圍，如設備的購置費用、人工費用等。其次，考慮時間和貸款利率。每年的運營成本是一筆不小的數字，多年的總和往往比固定部分投資大;多年的資金疊加需要考慮利率，將資金流折算為現值。再次，計算固定投資總成本、年運營費用、不同投資年的總成本及對應的累計偏差。最后，計算每年最小成本與其他運輸方式成本的比例關系、計算方案的被選概率，并進行數據分析，得到比選結果。

3 運輸方式的選擇

3.1 建立數學模型

設:(1)起終點之間物料可以被多種方式運輸;(2)各種費用可知，但是存在誤差;(3)運輸長度和線路長度已知;(4)建設的基礎條件相同且已知。

3.1.1 運輸成本公式

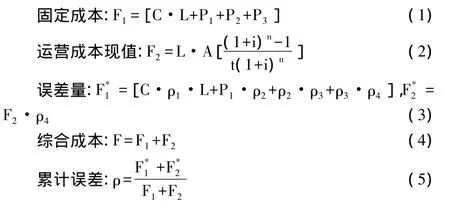
式中:C為單位線路造價(萬元)(誤差為ρ1);L為運輸線路長度(km);P1為車輛、加壓站、轉運站等費用總和(萬元)(誤差為ρ2);P2為附屬設施費用、建構筑無安裝費用總和(萬元)(誤差為ρ3);P3為其他費用，包括特殊地質處理費用(萬元)(誤差為ρ4);A為單位運輸成本(誤差為ρ5)(萬元);為利率為i、年限為n的折現公式。

3.1.2 運輸成本計算

假設所有條件已知，根據不同的時間，可得到成本矩陣F和對應的累計誤差ρ矩陣

式中:

Fij代表i年、第j種運輸方式的綜合成本;ρij代表i年、第j種運輸方式的綜合成本累計誤差

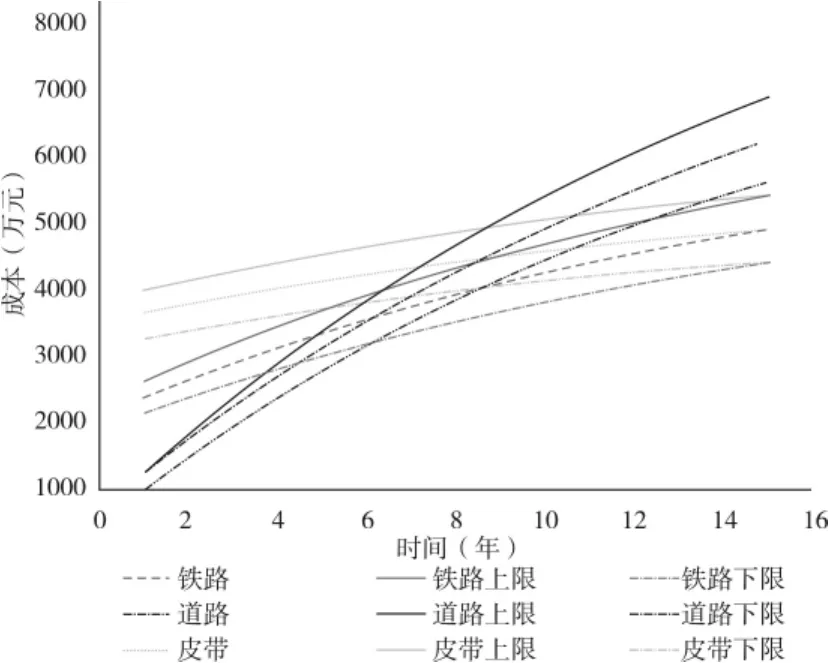
圖1 成本和時間關系

以時間為橫軸，以費用為縱軸，以(Fij，2i)為主要點，以[Fij×(1+ρij)，2i]為上限，以[Fij×(1－ρij)，2i]為下限，可以得到帶有誤差的“成本和時間關系圖”。如圖1為以鐵路、道路、皮帶三種運輸式的成本－時間關系圖。

3.1.3 運輸方式選擇

從上邊得到的成本和時間關系圖可以看出，每種成本由成本曲線、誤差上限和誤差下限三條曲線構成，且都以變化的曲率隨時間逐漸增大，每兩種成本都有一個交叉區域，在區域外部，運輸方式的比較十分明確，但在交叉區域內部，區分變得模糊。對于企業的建設，關注的是建設成本，規劃投資年的總成本(5年、10年、15年)，因此就需要對這幾個關鍵時間進行分析。

每種綜合運輸成本之間都存在一定的差值，差值越大則越容易做出比較，當兩個數值接近時就可能有同等的備選可能，這種狀態通過模糊選擇的方法能很好的解決。已知成本F、誤差下限F(1－ρ)誤差上限 F·(1+ρ)。對同一時間找出最小值和次小值，如第n個規劃年中最小值min(Fni)、次小值min次(Fni)。如圖2所示，在兩種方式的交叉區域內，A點位于方式2誤差上限和方式1下限的交叉點，定義此點處方式2的被選擇概率為1.0，方式1的被選擇概率為0;B點位于方式1和方式2的交叉點，被選擇概率均為0.5，且最小值與次小值轉換位置;C點位于方式1誤差上限和方式2誤差下限交叉點，方式1的被選概率為1.0，方式2的被選概率為0。則在交叉范圍內時間點n處。

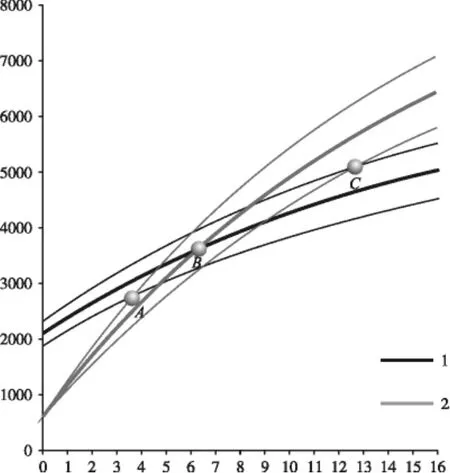
圖2 交叉區分析

min(Fnj)的被選概率為:

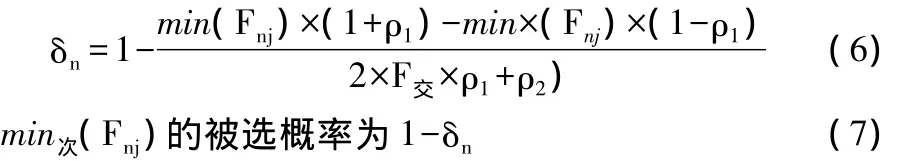
其中，p1對應min(Fnj)的方式和時間，p2對 min次(Fnj)中的方式和時間，F交指兩種方式交點處的值(B點)，有F交=F1=F2。

當出現多個范圍交叉時，進行多次運算，最終得到一個被選概率矩陣。對于概率矩陣δ，0表示不可能是最小，0～0.4表示有比較小的可能是最小，0.4～0.6表示有可能是最小，0.6～1.0表示很可能是最小，1.0表示肯定是最小。

計算成本矩陣F中每年最小值與其他值的對比矩陣，即:

對于對比矩陣K，0表示數值最小，0～0.2表示與最小值很接近，0.2～0.5表示與最小值比較接近，＞0.5表示與最小值偏離較大。

3.2 結果分析

選取n為0、5、10、15共4個時間，計算得到比矩陣和概率矩陣δ。

當一種運輸方式在δ中數值均大于0.4時，則此方式最優;

當一種運輸方式在δ中數值均小于0.4時，則此方式不是最優;

當一種運輸方式在δ中前5年小于0.4，其他大于0.4時，此方案最優;

當一種運輸方式在δ中前10年小于0.4，其他大于0.4時，放棄此方案;

當通過以上方式存在多種方案時，如果k中對應方案的差值在0.2以內的大于等于兩處，則對應時間的方案無法區分，反之，則選小的方案最優。

4 案例分析

一個鋼鐵企業從礦場到工廠的距離大概為2.0 km，運量為500×104(t/a)，可能存在4種運輸方式，已知技術條件見表1.(固定投資誤差均為0.2，單位運價誤差均為0.1，利率取0.065，資金全部轉化為現值。)

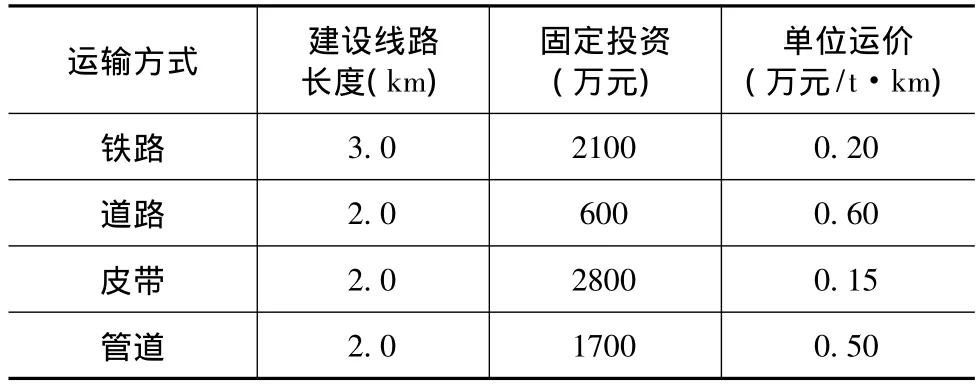
表1 經濟投資估算表

根據運輸方式計算公式得到0、5、10、15四個關鍵年的成本和對應累計誤差，并繪成本和時間關系，如圖3。

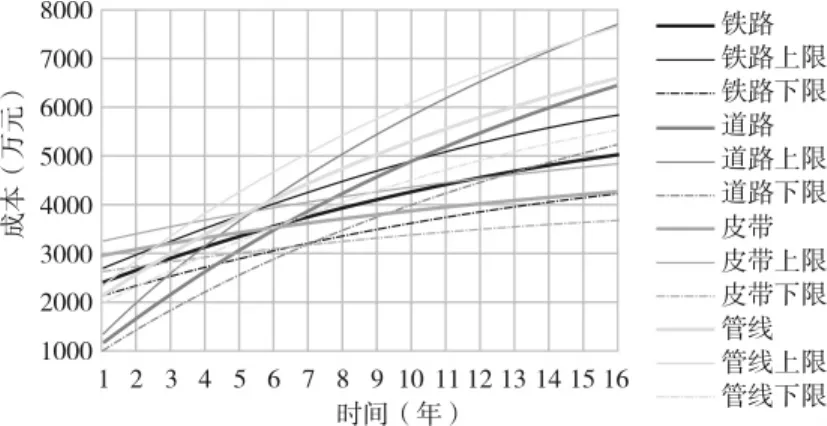
圖3 成本和時間關系

計算各種方式等價的交叉點

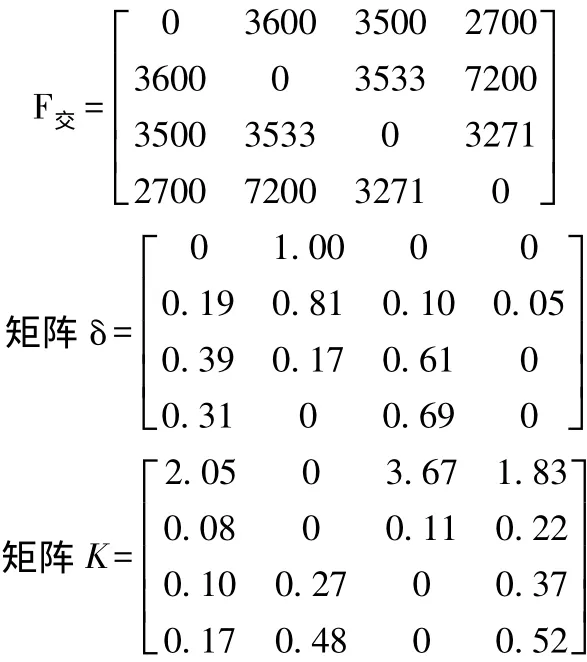
結果分析:在δ中，第一列:鐵路全部小于0.4，則非最優;第二列:道路前五年大于0.4，則非最優;第三列:皮帶前五年小于0.4，以后大于0.4，則皮帶運輸為最優;第四列:管線全部小于0.4，則非最優。

通過比較，得到一個最優結果為皮帶運輸方式，其各年總成本為(2800、3314、3878、4210)萬元，固定投資比鐵路多700萬元，15年動態成本節省711萬元;比道路固定投資多2200萬元，15年動態成本節省2032萬元;比管線固定投資多1100萬元，15年動態成本節省2191萬元。

5 總結

針對運輸方式的經濟比選，現狀做法是估算比選的數值直接比較，沒有引入誤差量，更沒有帶有誤差的比較方案，忽視了估算誤差對結果的影響。本文主要內容是在運輸方式的經濟比選時引入時間和誤差，通過計算最優方案和次優方案在帶有累計誤差時的被選概率，進行數據分析和模糊選擇，來確定最優方案。從一定程度上消減了估算誤差對最優方案的影響，且當誤差較大或數據較為接近時效果更為顯著。因此，此方法相對于一般的比選方法更具有可靠性，且可以提高比選精度。

但還存在一些問題，如怎樣對基礎數據估算時取合適的誤差量，一般沒有確定的數值或方法，多為假定量;模糊選擇時的區間劃分還不是很合理，需要根據具體情況而定，這里給出的只作為參考，另外針對企業內部車輛、設備的數量與運輸量之間的關系還沒有具體的研究;這些問題都給廠內運輸方式的選擇帶來很大的不確定性，因此對這方面還需要開展大量的研究。

[1]金琳.關于鋼鐵廠規模經濟性的一些看法[J].冶金經濟與管理，1990(21)

[2]馬建華.鋼鐵企業噸鋼運輸量分析及其控制策略[D].上海海事大學，2005

[3]楊秋俠.企業聯合運輸方式的選擇[J].公路與交通科技(應用技術版)，2007，12:157－159