凸輪檢測方法的誤差分析

申濤，劉興富

（1.西安工業大學，陜西西安 710032;2.廣州威而信精密儀器有限公司，陜西西安 710075）

1 概述

筆者提出的“敏感點法”，在發動機凸輪檢測中已被普遍采用。分析表明，“敏感點法”不但測算過程簡便，而且能滿足發動機凸輪的精密檢測要求。“敏感點法”所獲得的升程誤差檢測數據，在實際運用中符合“最小條件”要求。它是目前凸輪精密檢測的理想方法之一。

2 檢測方法原理

“敏感點法”是在“對稱最佳”原理的基礎上建立起來的。具體方法是:在凸輪“桃尖”兩側各任選一點a（αa，ha，h'a）和b（αb，hb，h'b），作為確定凸輪檢測位置的基準。由點a、b的理論正確升程ha、hb確定出點a、b的實際轉角φa、φb。理論和實踐均證明，當點a、b選在凸輪兩側的“敏感點”時，可以獲得凸輪的理想檢測位置，如圖1所示，其中上角*為等值誤差點。

凸輪檢測起始轉角φ0由以凸輪兩側“敏感點”為基準［1］求出

在凸輪檢查儀上按間隔點 （步長一般取為1°）進行檢測，得出凸輪的升程檢測數據。

下面對“敏感點法”的誤差進行分析:點a、b的升程誤差，可由升程函數表達式的全微分求得

點a、b的形狀誤差，必然影響式 （1）的正確性。如果將點a、b取在凸輪兩側的“敏感點”m、n時，并令Δhm=Δhn，可由式 （3）得到

式（1）～（4）中:

Δα為凸輪起始轉角誤差;

αm、αn為凸輪左、右側“敏感點”的理論轉角;

Δrm、Δrn為凸輪左、右側“敏感點”的形狀誤差;

hm、hn為凸輪左、右側“敏感點”的理論升程;

h'm、h'n為凸輪左、右側“敏感點”的升程變化率。

由式 （4）可知，Δ的大小不僅取決于點a、b形狀誤差的大小和方向，更重要的還取決于點a、b在凸輪輪廓上的位置。分析式 （4）:

（1）分子項越小，分母項越大，Δα越小。

（2）由分子項 （Δrm－Δrn）可以看出，Δα的大小與凸輪左、右側“敏感點”處的形狀誤差有關。筆者在測量實踐中發現，當凸輪處于理想檢測位置時，凸輪左、右側“敏感點”的升程誤差一般均為負值，這也就是加工中常說的“凹陷現象”，這是由于“敏感點”是切削速度和壓力角變化的轉折點的緣故。在一定加工工藝條件下，凸輪左、右側“敏感點”處的形狀誤差，產生的是同向誤差，且差值甚小，分子項最小;由分母項 （h'm－h'n）可以看出，因為凸輪左、右側“敏感點”的升程變化率的符號相反，絕對值最大，顯然，只有將點a、b取在凸輪左、右側的“敏感點”時，分母項最大。所以，這時Δα最小。

（4）綜上所述可知，“敏感點”是確定凸輪檢測位置的最理想的基準［2］之一。

3 凸輪檢測位置誤差引起的升程誤差

發動機凸輪的升程誤差，是凸輪形狀誤差的反映。檢測時，凸輪的理想形狀相對于實際形狀的位置應按“最小條件”來確定。即應使所獲得的檢測數據能保證凸輪升程誤差的最大值為最小。

如若被測凸輪是理想凸輪 （圖2）。設點c為凸輪理論轉角起始點，當測頭與點c相接觸，凸輪繞旋轉中心O轉過α角度時，測頭與凸輪輪廓上點d相接觸，升程為hd（圖2（a））;如果將凸輪旋轉一微小角度Δα，以點c1為凸輪檢測轉角起始點，仍轉過α角度時，測頭則由與點c1相接觸到與凸輪輪廓上點d1相接觸，測得的升程為hd1（圖2（b）），這時，由凸輪檢測位置誤差引起的誤差為

Δh0=hd1－hd

由于假設被測凸輪是理想凸輪，很顯然，誤差僅僅是由凸輪檢測位置誤差引起的

Δh0=h'·Δα

對于有形狀誤差的被測凸輪，誤差是形狀誤差 （通常由隨機誤差構成）與檢測位置誤差 （屬于系統誤差）的疊加，即

式中:Δr為凸輪輪廓的形狀誤差;

h'為凸輪升程變化率;

Δα為凸輪檢測位置誤差。

綜上所述，凸輪檢測位置誤差引起的誤差，具有如下規律:

（1）理想凸輪的誤差，純粹是由于凸輪檢測位置誤差引起的;有形狀誤差的被測凸輪誤差是凸輪形狀誤差與檢測位置誤差引起的誤差的疊加。

（2）當被測凸輪的檢測位置確定之后 （Δα已知），檢測位置誤差引起的升程誤差，凸輪輪廓上各被測點誤差大小各不相同，其值取決于各被測點升程變化率的大小。

（3）對整個凸輪而言，升程變化是非線性的，而對某一被測點則是線性的。

正確確定凸輪檢測位置的目的，是為了消除凸輪位置誤差的影響，實現凸輪真實形狀的反映。因此，檢測時必須使式（5）第二項中的Δα=0。當然，要做到這一點，是相當困難的。但是，在實際檢測中，“敏感點法”可以把Δα控制在非常小的范圍之內。使凸輪檢測位置誤差引起的誤差忽略不計。

4 凸輪檢測系統誤差引起的升程誤差

凸輪升程測量方程式可表達［3］為

對式 （6）微分

分析式 （7）可知，式中第一項Δα是由四部分組成:凸輪檢測位置誤差;被測凸輪偏心誤差;撥桿設計或安裝不合理引起的誤差;角度儀器的誤差。第二項中的=1，所以Δr0（基圓母線的形狀誤差）等值地反映升程誤差。

限于篇幅，文中不對式 （7）中第一、第二項進行分析，僅對第三、第四項具體分析如下。

4.1 檢測儀器誤差引起的升程誤差

凸輪的檢測，是由長度和角度儀器組成的檢測系統進行的。測量儀器誤差引起的升程誤差為

式中:h為凸輪被測點的升程;

h'為凸輪被測點的升程變化率;

φ為角度儀器的轉角。

4.2 被測凸輪偏心引起的升程誤差

當選用滾柱測頭 （0＜rp＜∞）時

當選用刀口測頭 （rp=0）時

當選用平面測頭 （rp=∞）時

式中:e為凸輪基圓偏心距;

r0為凸輪基圓半徑;

rp為測頭半徑;

α為凸輪轉角;

θ為凸輪基圓偏心方向角;

h為凸輪被測點升程;

hmax為凸輪最大升程;

h'為凸輪被測點的升程變化率。由式 （10）、（11）可知，Δh2是由轉角誤差和偏心誤差引起的誤差的和。當偏心方向角θ和被測凸輪升程變化率的絕對值較大的一側敏感點的位置相差90°時，由偏心誤差引起的升程誤差最大。

4.3 桿設計安裝不合理引起的升程誤差

被測凸輪安裝在角度儀器的頭尾頂針之間，由于被測軸線與儀器主軸軸線不重合 （如圖3所示），當撥桿設計或安裝不合理時，被測凸輪將產生一個轉角誤差而引起升程誤差［4］

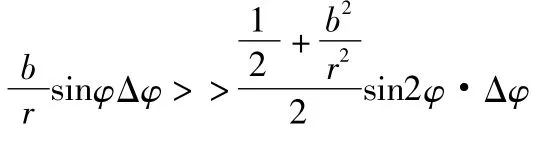
則

式中:b為撥桿球心與主軸頂尖間的軸向距離;

r為撥桿球心與主軸頂尖間的徑向距離;

φ為角度儀器的實際轉角;

Δφ為被測凸輪軸線與儀器主軸軸線間的夾角;

h'為凸輪被測點的升程變化率。

分析式 （12）可知:b≠0時，當 φ=0°、φ=180°時，Δh3=0;當φ=90°、φ=270°時，Δh3取得最大值;b≈0時，Δh3≈Δφ2。因此，撥桿的正確設計與安裝應引起特別重視。

4.4 測頭制造及安裝誤差引起的升程誤差

檢測對心式凸輪機構凸輪的升程時，應保證測頭中心、測量軸線、凸輪旋轉軸線處在同一平面，并保證測量軸線和凸輪旋轉軸線垂直。

（1）平面測頭垂直度、平面度誤差引起的升程誤差。

當測頭平面不垂直于測量軸線以及測頭的平面度誤差 （圖4）引起的升程誤差

由于測頭的平面度誤差與其引起的誤差等值，所以

式中:hc為被測點的升程檢測值;

h'為被測點的升程變化率;

Δc為平面測頭的垂直度誤差;

Δp為平面測頭的平面度誤差。

（2）滾柱測頭半徑誤差引起的升程誤差。

現以S195型柴油機的供油凸輪為例，由式 （8）可得:

凸輪輪廓的直線段 （0°≤α≤30°56'48″）

凸輪輪廓的頂圓段 （30°56'48″≤α≤63°22'10″）

凸輪輪廓的腹圓段 （63°22'10″≤α≤170°07'28″）

式中:α為凸輪轉角;

αc=54°50'50″為凸輪桃尖理論轉角;

αmax=170°07'28″為凸輪升程部分最大理論轉角;

Δrp為測頭半徑的誤差;

ld為基圓至頂圓中心距;

lf為基圓至腹圓中心距。

凸輪輪廓的基圓段 （170°07'28″≤α≤360°）是基準，其誤差為零。

（3）滾柱測頭 （刀口測頭）中心線和凸輪旋轉軸線不共面引起的升程誤差。

由圖5可得

因為

所以

式中:r0為凸輪基圓半徑;

rp為測頭半徑，刀口測頭時rp=0;

h為被測點的理論升程;

hc為被測點的升程檢測值;

Δ為凸輪旋轉中心與測頭中心移動軌跡平面間的距離。

4.5 檢測系統不符合阿貝原理引起的升程誤差

在凸輪檢測中，無論是平面測頭還是滾柱測頭，測頭和凸輪的接觸點，除基圓部分、“桃尖”外，凸輪輪廓的其他部分均不通過測量軸線。當接觸點偏離測量軸線時，檢測系統不符合阿貝原理 （圖6），由此引起的誤差為

當選用平面測頭時，p=h'

式中:p為接觸點偏離測量軸線的距離;

l為測頭中心至前支承的間距;

L為測軸兩支點的間距;

Δb為測軸配合最大間隙。

5 凸輪檢測方法標準誤差

當檢測系統、被測凸輪、測頭制造、安裝及測力、溫度等因素引起的升程誤差在某一定范圍時，可求出凸輪檢測方法的標準誤差［5］:

當用平面測頭時

當用滾柱測頭時

當用刀口測頭時

凸輪檢測方法的極限誤差:

6 結束語

在JJ2—JJF2數字顯示式凸輪測量儀 （角值 1″，線值1 μm）上測量凸輪的升程，以普遍應用的S195型柴油發動機圓弧凸輪為例，對凸輪檢測方法的誤差進行了分析。應該說明，文中方法對于發動機高速領域中的各種函數凸輪同樣適用。

【1】劉興富.試論凸輪檢測起始轉角的求解方法［J］.臺北:機械技術，2002（12）:145－150.

【2】劉興富.凸輪檢測數據的基準轉換處理方法［J］.制造技術與機床，2001（9）:29－33.

【3】劉興富.發動機凸輪誤差測量數據的計算機處理方法［J］.汽車零部件，2008（6）:69－72.

【4】劉興富.試論凸輪測量步長的優化設計方法［J］.汽車零部件，2011（1）:60－61.

【5】劉興富.凸輪軸自動測量儀精度認定方法的探究［J］.汽車零部件，2011（8）:64－67.