平面點集Delaunay三角剖分的分治算法

謝增廣

（華北計算技術研究所，北京100083）

0 引 言

三角剖分是計算幾何中領域的重要課題之一。平面點集Delaunay三角剖分與該點集的Voronoi圖是對偶圖，具有許多優良性質，在圖形網格化技術領域有著廣泛應用。三角剖分算法理論研究已經相當成熟，已經能夠證明算法時間復雜度的上界和下界［1］，然而由于區域拓撲劃分問題，算法在實際工程中應用的難易程度有所不同。根據實現過程，Delaunay三角剖分的算法可以分為逐點插入法、三角網生長法，分治算法等，其中分治算法最適合實際工程應用。

論文引入了一種數據結構——雙鏈接邊表 （doublyconnected edge list，DCEL），利用該數據結構可以方便地對平面區域進行劃分；引入了3個工具算法，簡化了Delaunay三角剖分算法分治的實現過程；另外對特殊退化情況進行分類處理，增強了該算法的實用性。

1 算法設計與實現

1.1 數據結構

雙鏈接 邊 表 （doubly－connected edge，DCEL）［4－5］是 用來表示平面圖拓撲信息的一種數據結構，如圖1所示。

在DCEL中，將每條邊的兩端分別作為一條半邊。半邊有方向性，由起點出發，指向另一個端點。一條邊的兩條半邊互為孿生半邊。

DCEL由三組記錄構成，分別存儲頂點、面、半邊的信息。

（1）在頂點V的記錄中，除了存儲點的坐標信息，還有一個指向半邊的指針，指向以V為起點的某一條半邊。

（2）在面f的記錄中，只存儲了一個指向半邊的指針，指向該面邊界上的某一條半邊。

圖1 DCEL數據結構

（3）在半邊edge的記錄中，存儲了半邊的起點，一個半邊的指針指向其孿生半邊，一個面指針指向位于半邊左側的面face。此外還有2個半邊指針，分別指向沿著face邊界方向的前一條半邊和后一條半邊。

根據DCEL提供的信息，可以很方便地對平面進行子區域劃分。為了簡化分治Delauany三角剖分算法實現過程，不必存儲面的信息。

1.2 預備工具算法

介紹分治Delauany三角剖分算法之前，先引入3個預備工具算法：判斷點是否在指定三點外接圓內，判斷夾角不大于π，求不相交的2個凸多邊形的上下公切線。

1.2.1 判斷點是否在指定三角形的外接圓內

設不共線三點a，b，c構成的三角形記作△ （a，b，c），點的d｛a，b，c｝。判斷d是否在△ （a，b，c）外接圓內的方法是［6］：記ret＝，ret＜0，d在△ （a，b，c）外接圓外部；ret＝0，d在△ （a，b，c）外接圓邊界上；ret＞0，d在△ （a，b，c）外接圓內部。

定義操作inCircle（a，b，c，d），如果d在a，b，c確定的三角形外接圓內，返回TRUE；否則，返回FALSE。顯然地，inCircle（a，b，c，d）的時間復雜度為O （1）。

1.2.2 判斷夾角不大于π

設不共線三點為a，b，c，記逆時針方向夾角∠abc為θ，θ與π大小關系判斷方法是［6］：記ret＝，假定人沿著方向行走，如果c在其左側，ret＞0，θ＜π；如果c在其右側，ret＜0，θ＞π；如果c在方向上，ret＝0，θ＝π。

1.2.3 求不相交的2個凸多邊形的上下公切線

設左邊的凸多邊形為LP，右邊的凸多邊形為RP，如圖2所示。記L為LP邊界上的最右邊的頂點，R為RP邊界上的最左邊的頂點；記LP和RP的上公切線是tct（top common tangent），TL在LP的邊界上，為tct的左端點，TR在RP的邊界上，為tct的右端點；記LP和RP的下公切線是bct（bottom common tangent），BL在LP的邊界上，為bct的左端點，BR在RP的邊界上，為bct的右端點。為上公切線，當且僅當LP邊界上的點和RP邊界上的點均不在的左側；同理，為下公切線，當且僅當LP邊界上的點和RP邊界上的點均在的左側。

圖2 求2個不相交凸多邊形的上下公切線

為了更好地說明該算法，設點V為凸多邊形P邊界上的一點，定義下面2個操作：①ccw （V，P），V沿著P邊界逆時針方向移動到達的第一個點；②cw （V，P），V沿著P邊界順時針方向移動到達的第一個點。

zig－zag算法

輸入：左側凸多邊形LP，右側凸多邊形RP。LP和RP不相交。

輸出：LP和RP的上下公切線。

Begin

步驟1 L為LP邊界上的最左點，R為RP邊界上的最右點。L1＝L，R1＝R，L2＝L，R2＝R。

步驟2 若toLeft（L1，R1，cw （R1，RP））為真，R1＝cw （R1，RP）；若toLeft（L1，R1，ccw （L1，LP））為真，L1＝ccw （L1，LP）。迭代這一過程，直至LP邊界上的點和RP邊界上的點均不在的左側。

步驟3 若toLeft（L2，R2，ccw （R2，RP））為假，R2＝ccw （R2，RP）；若toLeft （L2，R2，cw （L2，LP））為假，L2＝cw （L2，LP）；迭代這一過程，直至LP邊界上的點和RP邊界上的點均在的左側。

End

zig－zag算法執行的次數只與LP的右半邊界上的點和RP的左半邊界上的點規模有關。設點集規模為N，zigzags算法時間復雜度不超過O （N）。

定義操作zig－zag（LP，RP），得到LP和RP的上公切線為tct，下公切線為bct。

1.3 分治Delauany三角剖分算法

分治Delauany三角剖分算法的基本步驟如下：

（1）點集初始化：將點集以橫坐標為主，縱坐標為輔按升序排序。

（2）將點集劃分為近似相等的兩個子點集。

（3）分別對兩個子點集進行Delauany三角剖分。

（4）合并兩個子點集的Delauany三角網。

（5）遞歸執行步驟 （2）到步驟 （4），直至點集的所有點都參加了Delauany三角網的構造。

由排序算法時間復雜度可知，點集初始化算法時間復雜度為O （N＊logN）。點集初始化之后，將點集合劃分，直至每個子點集合的規模不超過3個；對這些子點集三角化，得到點、線段或者三角形，如圖3所示。

圖3 點集初始化和點集合劃分

點集初始化后，設點集存儲為數組P［］。定義以下2個操作：

（1）Merge （LDT，RDT）：LDT 為 左 側 子 點 集Delauany三角剖分后得到的結果，RDT為右側子點集Delauany三角剖分后得到的結果，Merge是合并操作。該操作返回合并LDT和RDT之后得到的Delauany三角剖分后的結果DT。合并是分治Delauany三角剖分算法的核心，會在下一節合詳細闡述。

（2）Delauany＿Triangulate（start，end）：start為點集的起始點編號，end為點集的終結點編號，Delauany＿Triangulate是分治操作。該操作將點集劃分為若干子點集，使得每個子點集的數量不超過3個，并對子點集進行三角化；對相鄰的點集構成的簡單凸多邊形迭代地進行Merge操作合并，直至得到點集的Delauany三角剖分的結果。該操作返回點集的Delauany三角剖分的結果，設為DT。

分治算法偽代碼如下：

Delauany＿Triangulate（start，end）

｛

if（1＝＝end－start＋1）//只有1個點

｛

將Pstart放入DT，return DT；

｝

else if（2＝＝end－start＋1）//只有2個點

｛

｝

esle if（3＝＝end－start＋1）//只有3個點 （3點共線為退化情況，暫不考慮）

｛

｝

else //多于3個點，進行分治

｛

mid＝ （start＋end）/2；

//LDT表示左邊點子集Delauany＿Triangulate后得到的結果

LDT＝ Delauany＿Triangulate（start，mid）；

//RDT表示右邊點子集Delauany＿Triangulate后得到的結果

RDT＝ Delauany＿Triangulate（mid＋1，end）；

//合并LDT和RDT，得到結果DT

DT＝ Merge（LDT，RDT）；

｝

return DT；

｝

1.3.1 合并算法

設DT是合并LDT和RDT的結果。如圖4所示，DT中的邊分為3類：

（1）LL－edge：在Delauany三角剖分左子點集結束得到LDT時，LL－edge已經被創建，且LL－edge∈LDT；顯然的，LL－edge的兩個端點 ∈LDT。

（2）RR－edge：在Delauany三角剖分右子點集結束得到RDT時，RR－edge已經被創建，且RR－edge∈RDT；顯然的，RR－edge的兩個端點∈RDT。

（3）LR－edge：LL－edge是在合并LDT和 RDT過程中被新創建的，且LR－edge∈DT；在DT中，LR－edge是Delauany邊；在創建LR－edge之前，LR－edge的左端點 ∈LDT，LR－edge的右端點∈RDT。

在合并過程中，由于創建LR－edge，可能會刪除若干LL－edge和 RR－edge，且已經刪除的 LL－edge或 RR－edge不會再生成；合并過程中，不會創建新的LL－edge和RR－edge。

對圖3中劃分的點集合進行合并，得到圖4。由于劃分的各個子點集三角化后，得到最簡單的凸多邊形 （點，線段，三角形），此次合并并沒有刪除LL－edge和RR－edge。

圖4 合并后的邊分為LL－edge，RR－edge，LR－Edge

為了詳細闡述合并算法且不失一般性，下面對圖4的左子點集Delauany三角剖分和右子點集Delauany三角剖分進行合并。

合并算法初始化時記DT＝LDT∪RDT。Delauany三角剖分得到的閉合邊界就是點集構成的凸包，因此LDT和RDT的上下公切線在DT中。

記下公切線形成的LR－edge為Base LR－edge，上公切線形成的LR－edge為Roof LR－edge，如圖5所示。

圖5 合并初始化，Base LR－Edge和Roof LR－edge

合并算法的核心是從Base LR－edge向上搜索LR－edge，將其加入到DT中，直至到達Roof LR－edge為止。在這一過程 中，可能使 LL－edge或 RR－edge不 再 是 DT 中 的Delauany邊，因此這樣的LL－edge或RR－edge需要從DT中刪除。

為了闡述合并算法，記DT為平面點集的Delauany三角剖分，定義以下5個操作：

根據DCEL數據結構的特性，以上5個操作可以在O（1）時間完成。

記New LR－edge的左端點為L，右端點為R。初始化時，L為下公切線的左端點，R為下公切線的右端點。New LR－edge從Base LR－edge開始向上尋找下一個LR－edge，記為Next LR－edge。Next LR－edge的一個端點是L或R，另一個端點記為V。因此根據LR－edge定義，只需要確定端點 V （VNew LR－edge），就可以確定Next LR－edge。

可以證明，V是L或R的鄰點。所謂L的鄰點，也稱作LDT關于L的候選點，是指該點和L為端點的線段是LL－edge；同理，所謂R的鄰點，也稱作RDT關于R的候選點，是指該點和R為端點的線段是RR－edge。否則，如果V不是L或R的鄰點，則New LR－edge會與LL－edge，或RR－edge，或其它的LR－edge相交，這不符合三角剖分的基本性質。

為了進一步確定V的搜索范圍，V只能在2個點之間選擇，一個是L的某個鄰點，也稱為LDT關于L的最終候選點 （final candidate）；另一個是R的某個鄰點，也稱為RDT關于R的最終候選點。

1.3.2 選取候選點

為了詳細闡述尋找V的過程且不失一般性，先尋找RDT中關于R的最終候選點。記RDT中關于R的第一潛在候選點 （first potential candidate）R1，R1是R鄰點Ri中與線段以R為軸點順時針方向構成夾角∠LRRi最小的點；記RDT中關于R的次潛在候選點 （next potential candidate）R2，R2是R鄰點Ri中與線段以R為軸點順時針方向構成夾角∠LRRi次小的點。如圖6所示。

第一潛在候選點是否是最終候選點，需要經過以下2條判定規則檢驗：

（1）向上搜索判定：第一潛在候選點R1與邊順時針方向夾角∠LRRi＜π。向上搜索判定保證尋找LR－edge的過程是從下公切線逐點向上，直至到達上公切線為止。

圖6 RDT關于R的最終候選點的選取

（2）外接圓判定：由第一潛在候選點R1，New LR－edge的左右端點L，R三點確定的外接圓不包含次級潛在候選點R2。外接圓判定保證Delaunay剖分的正確性。

如果 （1）和 （2）都滿足，則R1是RDT關于R的最終候選點；如果 （1）不滿足，則搜索LR－edge過程已經達到了Roof LR－edge的右端點，RDT中關于R的候選點不必考慮，即沒有可以選擇的候選點；如果 （1）滿足，而 （2）不滿足，則從DT中刪除線段所表示的 RR－edge，R1＝R2，即次潛在候選點作為第一候選點，迭代這一處理過程直至找到最終候選點或者沒有可以選擇的候選點結束，如圖6所示。尋找RDT候選點的算法描述如下：

Begin

步驟1 R1＝cw＿rotate（R，L，RDT），若toLeft（L，R，R1）為真，執行步驟2；否則執行步驟3。

步驟2 R2＝cw＿rotate（R，R1，RDT），若inCircle（L，R，R1，R2）為真為RR－edge，需要從DT中刪除，delete＿RR （R，R1，DT），R1＝R2，R2＝cw＿rotate（R，R1，RDT）；迭代這一過程，直至inCircle （L，R，R1，R2）為假。R1是RDT最終候選點。

步驟3 RDT中沒有候選點

End

同理，鏡像地可得到LDT中關于L的最終候選點，如圖7所示。

圖7 找到LDT關于L的最終候選點

尋找LDT候選點的算法描述如下：

Begin

步驟1 L1＝ccw＿rotate（L，R，LDT），若toLeft（L，R，L1）為真，執行步驟2；否則執行步驟3。

步驟2 L2＝ccw＿rotate（L，L1，LDT），若inCircle（L，R，L1，L2）為真，為LL－edge，需要從DT中刪除，delete＿LL （L，L1，DT），L1＝L2，L2＝ccw＿rotate（L，L1，LDT）；迭代這一過程，直至inCircle（L，R，L1，L2）為假。L1是LDT最終候選點。

步驟3 LDT中沒有候選點

End

1.3.3 確定LR－edge

根據LDT關于L的最終候選點和RDT中關于R的最終候選點的存在性，分以下4種情況確定LR－edge：

（1）如果RDT中關于R沒有可以選擇的候選點，且LDT中關于L沒有可以選擇的候選點，則線段表示的LR－edge為Roof LR－edge，合并過程結束。

（2）如果RDT中關于R的最終候選點是R1，且LDT中關于L沒有可以選擇的候選點，則V＝R1，邊是LR－edge，需要加入到DT中。

（3）如果RDT中關于R沒有可以選擇的候選點，且LDT中關于L的最終候選點是L1，則V＝L1，邊是LR－edge，需要加入到DT中。

（4）如果RDT中關于R的最終候選點是R1，且LDT中關于L的最終候選點是L1，則需要對L，R，L1，R1這4個點進行Delaunay三角形測試，如圖8所示。如果L1在△ （L，R，R1）外接圓的外部，則 V＝L1，邊是LR－edge，需要加入到DT中；否則 V＝R1，邊是LR－edge，需要加入到DT中。

由此LR－edge向上尋找下一個LR－edge，迭代上述合并處理流程，在到達Roof LR－edge時合并結束，得到點集的Delauany三角剖分，如圖9所示。

1.3.4 合并算法偽代碼及算法復雜度分析

綜上所述，合并算法偽代碼如下：

Merge（LDT，RDT）

｛

DT＝LDT∪RDT；//初始化操作

zig－zag （LDT，RDT）得上公切線Roof＿LR－edge，下公切線Base＿LR－edge；

點L＝Base＿LR－edge的左端點，點R＝Base＿LR－edge的右端點；

insert＿LR （L，R，DT）；//將Base＿LR－edge加入到DT中

while（不是 Roof＿LR－edge）//向上搜索LR－edge，在到達Roof＿LR－edge時終止

｛

分別尋找LDT和RDT候選點L1，R1；

根據左右候選點L1，R1的存在性確定新的LR－edge并刪除無效的LR－edge，搜索向上進一步；

｝//end while

Merge結束，得到得到點集的Delauany三角剖分，return DT；

｝

Merge算法的執行分為以下3種操作：

（1）Merge初始化。用zig－zag算法尋找上下公切線，算法復雜度不超過O （N）。

（2）刪除LL－edge或RR－edge。在搜索LR－edge過程中刪除的LL－edge或RR－edge的數量為常數。

（3）加入LR－edge。Merge生成 LR－edge的過程與zigzag類似。記點集U＝左Delauany三角剖分右邊界上的點∪右Delauany三角剖分的左邊界上的點。U的規模不超過N，而建立LR－edge的次數與點集U的規模是線性關系，所以加入LR－edge的次數不超過N。

綜上所述，Merge算法的時間復雜度為O （N），分治的復雜度為O（1）。設分治Delauany三角剖分算法的總的時間復雜度為T （N），則T （N）＝2T （N/2）＋O （N）。根據主定理［9］，分治Delaunay三角剖分算法的時間復雜度為O （N＊LogN）。

1.3.5 退化情況處理

一般地，退化情況在邊界值判斷時候出現。

（1）對于toLeft（A，B，C）操作，A，B，C三點共線是退化情況。為此，增加一個判斷共線的操作coLine（A，B，C）操作。在點集合劃分子點集時，如果子點集的規模是3，且這三點共線，則此子點集三角化應該得到2條邊。在此基礎上，三點共線的退化情況不會影響算法的正確性。

（2）對于inCircle（A，B，C，D）操作，A，B，C，D四點共圓是退化情況。在合并過程中，四點共圓形的退化情況不會影響整個算法的正確性。

2 實驗與結果分析

針對不同點集規模，每個數量級進行5次運算，算法運行的平均時間見表1，根據實驗結果進行曲線擬合如圖10所示。

表1 實驗結果數據

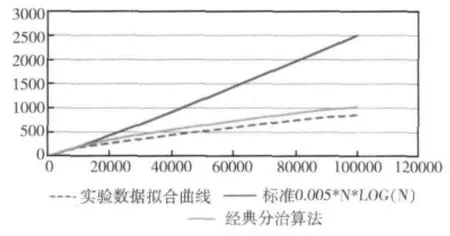
圖10 時間復雜度曲線擬合

頂部實線表示由公式0.0005＊ N＊LOG （N）得到的曲線，而虛線表示實際中測得的平均運行時間。從圖中實際數據擬合曲線與標準曲線的接近程度，表明程序運行時間的變化規律符合O （N＊logN）這一趨勢，與算法的復雜度為O （N＊logN）的理論結果相一致。

中間的實線是經典分治算法實驗者測得的平均運行時間。因為采用了zig－zag算法，簡化了求不想交凸多邊形上下公切線的過程，并且DCEL數據結構特性使合并算法中的若干操作都是O （1），從而整個算法的效率較經典算法提升了約5%。

3 結束語

本文使用DCEL數據結構表示平面點集Delaunay三角剖分的結果；闡述了分治Delaunay三角剖分算法，并利用zig－zag算法尋找不相交凸包上下公切線簡化了算法的實現。并且對退化情況進行分類處理，增強了算法的實用性。

在實際工程中，Delauany三角剖分的模型會更復雜，實現難度大，其中具有代表性的模型有平面點集含特征約束的Delauany三角剖分和三維空間的Delauany三角剖分，值得進一步深入研究。

由于DCEL數據結構不僅能有效地對平面點集進行子區域劃分，而且可以存儲三維空間的拓撲信息，本論文為復雜的問題模型研究與實際應用奠定了基礎。

［1］Mark de Berg，Otfried Cheong，Marc van Kreveld，et al，Computational Geometry：Algorithm and Applications ［M］.3rd ed.DENG Junhui，transl.New York：Springer－Verlag Berlin Heidelberg，2008：197－218 （in Chinese）. Mark de Berg，Otfried Cheong，Marc van Kreveld，等.計算幾何—算法與應用 ［M］.3版.鄧俊輝，譯.北京：清華大學出版社，2009：250－285.

［2］ZHOU Jia－wen，XUE Zhi－xin，WAN Shi.Survey of triangulation methods ［J］.Computer and Modernization，2010，26（7）：75－78 （in Chinese）.［周佳文，薛之昕，萬施.三角剖分綜述 ［J］.計算機與現代化，2010，26 （7）：75－78.］

［3］Doubly－connected edge list ［EB/OL］. ［2011－04－18］.http：//en.wikipedia.org/wiki/Doubly＿connected＿edge＿list.

［4］Ryan Holmes.The DCEL data structure for 3Dgraphics［EB/OL］.［2009－09－27］.http：//www.holmes3d.net/graphics/dcel/.

［5］Max McGuire.The half－edge data structure ［EB/OL］.［2000－08－07］.http：//www.flipcode.com/archives/The ＿ Half－Edge ＿Data＿Structure.shtml.

［6］Guibas L，Stolfi J.Primitives for the manipulation of general subdivisions and the computation of Voronoi diagrams ［J］.ACM Transactions on Graphics，1985，4 （2）：75－123.

［7］Rex A Dwyer.A faster divide－and conquer algorithm for constructing Delaunay triangulations［J］.Algorithmica，1987，2（2）：137－151.

［8］Lee D T，Schachter B J.Two algorithms for constructing a Delaunay triangulation ［J］.International Journal of Computer and Information Sciences，1980，9 （3）：219－242.

［9］Thomas H Cormen，Charles E Leiserson，Ronald L Rivest，et al.Introduction to algorithms［M］.PAN Jingui，GU Tiecheng，LI Chengfa，et al transl.2nd ed.MIT Press，2001：43－49 （in Chinese）.Thomas H Cormen，Charles E Leiserson，Ronald L Rivest，等.算法導論 ［M］.2版.潘金貴，顧鐵成，李成法，等譯.北京：機械工業出版社，2011：43－49.

［10］WANG Li.Research on triangulation algorithm ［D］.Shanghai：Shanghai Jiaotong University，2010 （in Chinese）. ［王力.三角剖分算法研究 ［D］.上海：上海交通大學，2010.］