基于數據統計診斷的截面數據診斷方法
杜聰慧,崔永偉,李子奈
0 引言
由于計量經濟學是利用樣本建立、估計、檢驗模型的,樣本數據質量好壞是決定模型質量的關鍵因素,所以,拿到數據后,首先要檢查數據質量。針對時間序列數據的診斷很多學者對此已做了研究,并找到了好的方法進行鑒別,而對截面數據的診斷研究甚少,因為一批發生在同一時間截面上的截面數據大多是通過調查而得到的,能夠得到數據已經不易,很少有人對數據的質量進行診斷。而在利用截面數據進行計量分析中,只有當數據是在截面總體中由隨機抽樣得到的樣本觀測值,并且被解釋變量具有連續的隨機分布時,才能夠將模型類型設定為經典的計量經濟學模型,由此可見,經典計量經濟學模型對截面數據存在著很強的依賴性。根據近代回歸分析中的數據診斷理論,探索對統計推斷(如參數估計、預測)有較大影響的觀測數據稱為是數據統計診斷[1]。基于此,本文擬從數據統計診斷角度嘗試探討診斷截面數據的方法,以期將混擬在其中的異常數據尋找出來,從而增加計量經濟分析結果的可靠性。
1 反常結果判別法
反常結果是數理統計學中的概念。它是指某一變量的觀測數據中有時出現個別相對特別大或特別小的數據,這些數據稱為反常結果。一個反常結果可能只是數據中內在的隨機變異性的一個極端表現,也可能是因為觀測錯誤、記錄錯誤等非隨機因素造成的。如果是前一種情況,它就必須保留下來與其它數據接受同樣的處理;如果是后一種情況,在分析問題時就必須舍棄這些數據。保留或舍棄一個反常數據都需要經過檢驗來決定。其檢驗方法稱為反常結果判斷法。
反常結果判斷法包括方差比法、極值偏差法和極差比法(即Dixon準則)等三種基本方法。通常的數據統計整理方法往往都對樣本數據有一個前提假設,即樣本數據來自同一個總體。這里假設總體分布為正態分布N(μ,σ2),樣本容量大小為n,先將數據按從小到大的次序排序,記成
1.1 方差比法[2]
1.2 極值偏差法[2]
首先構造統計量

其中En(或E1)是n個數據結果中,剔除可疑數據x(n)(或x(1))后所得的總體中間誤差E的估計,即
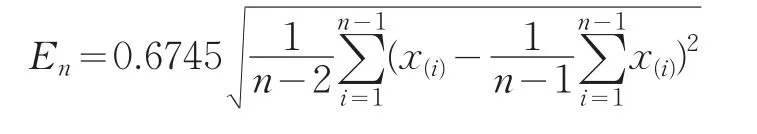
對于n個數據結果,給定顯著水平α,由Q分布臨界表中查出Qα,若Q>Qα,則可認為 x(n)(或 x(1))為異常值。
1.3 極差比法[3]
(1)半極差型
如果x(n)(或x(1))是異常數據,則它們應遠離其均值,于是利用統計量或,其中,這兩種情形下的統計量均為單側檢驗統計量,若不知異常數據在上側還是在下側,則需進行雙側檢驗,其統計量為
(2)極差型
如果樣本數據存在異常數據,則極差x(n)-x(1)比起σ或S來,會過分的偏大,于是可用統計量來檢驗數據中是否存在異常數據。但這種方法的缺點在于當判斷出樣本中存在異常數據時,卻沒能判別出x(1)和x(n)中到底是哪一個為異常數據。
(3)鄰差型(狄克遜準則)
在樣本中,若x(n)是異常數據,那么以其標準差σ(當σ未知時以σ的估計S)為刻度,它應離鄰近的數據x(n-1)較
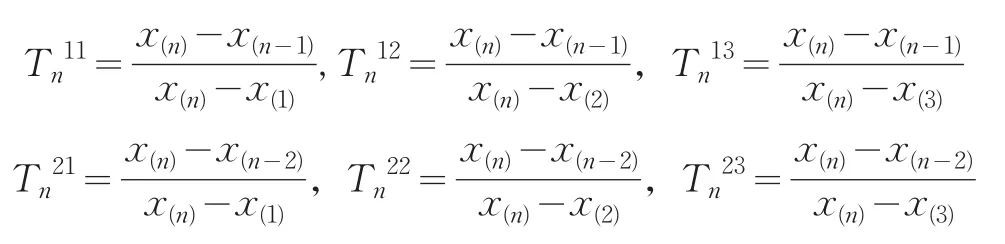
由于當樣本數n較大時,極差x(n)-x(1)中包含的σ的信息較少,使得檢驗功效降低,于是可用擬極差x(n)-x(2),x(n)-x(3)來代替。一般認為當3≤n≤7時,以,當 σ未為佳;當8≤n≤10時,以為佳;當11≤n≤13時,以為佳;當14≤n≤30時,以為佳。
具體檢驗時,當Tn大于某個常數C2n時,就判斷x(n)是異常數據,其中C2n滿足P{Tn>C2n}=α,當概率值小于給定的α時,就認為x(n)是異常數據;否則認為不是。
在實際應用中,半極差模型和鄰差模型檢驗法用的較多,鄰差模型檢驗法是一種較好的方法。
2 利用跳躍度來檢驗異常值
先引入跳躍度的概念。設X(1),X(2),…,X(n)為來自總體分布F(X;θ)的樣本容量為n的次序統計量,為僅依賴于X(1),X(2),…,X(k)的期望μ的點估計,則稱為在點k的跳躍度(簡稱k點的跳躍度)[4]。
任何一組n個數據都可以看作是來自某一總體樣本容量為n的樣本觀察值,將它們進行由小到大的排序后異常值必居于數據所組成的數列兩端。且異常值的存在必使期望的點估計產生跳躍,因而期望點估計的最大跳躍點(跳躍度最大的點)最有可能是異常數據的起始點。具體做法如下:
(1)將各數據按由小到大的次序進行排列,并計算出各點的跳躍度;
(2)找出兩端跳躍度的最大值點;
(3)進行比較分析,若跳躍度的最大值與相鄰跳躍度確有明顯差異,那以左側對應的統計數據為最大的異常小值,右側對應的統計數據為最小的異常大值。這樣,就可較方便地把混雜在數據中的異常值剔去。
利用跳躍度來檢驗出異常值后,即可利用剩余下的正常數據由經典統計的方法進行統計分析,但值得注意的是,在理論上被剔除的異常值是相對于一定的精度而言的,畢竟這些異常數據和其它數據一樣也來自于同一總體,因此或多或少的會帶來一些總體的信息。為提高統計分析的可靠性,如果有先驗信息可用的話,在進行統計分析時用貝葉斯方法效果會更好些。
3 預測區間判斷法與羅曼諾夫斯基準則
3.1 預測區間判斷法[5]
對同一變量對不同的對象進行測量,測量數據一般符合正態分布,設x1,x2,…,xn是來自X的一個樣本值,并且它們獨立同分布,且X~N(μ,σ2),根據期望與方差的點估計理論,構造統計量,對于給定的α,查t分布表,的的值,得 μ的置信度是1-α的置信區間,而μ落在該區間之外的概率很小,屬于小概率事件,在正常的測量過程中不會發生。因此取為 臨 界 值 ,若 xi(i=1,2,…n)滿 足,則xi可判斷為是異常數據。
3.2 羅曼諾夫斯基準則
一般處理數據前,認為數據服從正態分布,但是數理統計學可以證明,在測量次數較少的情況下,t分布更符合實際分布,在吳天鵬(1995)提出了一個新的準則,該準則就是以t分布為依據建立的,在一定測量次數n下,設獨立測得的一組x1,x2,…,xn,若對某一數據xk有懷疑,可按照以下步驟判別[11]:
(1)先將懷疑數據xk去掉,計算出不包含xk的數據的算術平均值
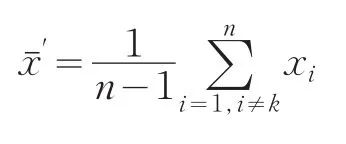
(2)計算出不包含xk的殘差在內的標準差
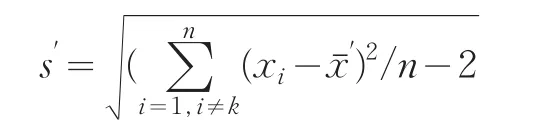
(3)根據選定的顯著性水平α和數據的個數n,在t分布表中查出檢驗系數 K(α,n),δ=K(α,n)s′;
文獻[11]將預測區間判斷法與羅曼諾夫斯基準則剔除異常數據做了比較,發現預測區間判別法診斷出的異常數據多于羅曼諾夫斯基準則。羅曼諾夫斯基準則是比較成熟的判斷準則,它建立的基礎符合數理統計理論的有關的結論,剔除異常數據時比較謹慎,在測量次數較少(n≤10)時,使用此準則比較可靠。
4 結束語
基于數據統計的診斷方法是對給定的數據集合假設一個分布或概率模型(例如一個正態分布),然后根據模型采用不一致檢驗來確定異常。而在大多數情況下,數據集合參數分布可能是未知的,所以,當沒有特定的檢驗時,基于統計的這些檢驗方法不能確保發現所有的異常,或者觀測到的分布不能恰當地被任何標準的分布來模擬。
在診斷出異常點以后,不要簡單地將異常數據刪除,因為這樣做可能將異常點攜帶的一些有用的信息丟失,如在經濟領域,異常值的出現可能是某種預警信息的表現等,所以應該對不同情況的異常點給予不同處理。如果證實是數據錄入錯誤,可以刪除。保留或舍棄刪除一個異常數據都需要經過檢驗來決定。
[1] 石磊.多水平模型及其統計診斷[M].北京:科學出版社,2008.
[2] 趙崮巍.異常數據的判定方法及結果處理[J].現代商檢科技,1993,(3).
[3] 杭愛明.如何處理統計數據中的異常值問題[J].上海統計,1994.
[4] 張德然.統計數據中異常值的檢驗方法[J].統計研究,2003,(5).
[5] 邵婷婷等.兩種剔除異常數據的方法比較[J].現代電子技術,2008,(24).

