基于仿真技術小型液壓搗固機液壓系統的研究

王 楊，杜海若

（西南交通大學 機械工程學院，1.碩士研究生，2.教授 四川 成都 610031）

鐵路道床的搗固作業，是鐵路養路工作的關鍵工序之一［1］。我國大型養路機械從上世紀80年代投入使用，至今已初具規模。但是大型養路機械具有局限性，使用成本高，天窗時間要求較長。因此，對一些小型的養護任務顯得不符合實際意義和經濟效益。而中小型的養護機械就具備了靈活便捷的優勢，其發展也具有現實意義。XYD小型液壓搗固機就是用于鐵路保養、維修以及新建道床搗固作業的專用小型機械，具有操作方便，使用靈活等優點。

以往的液壓系統主要是憑借工程師自身的知識、經驗及試驗進行設計及改進，而結構參數對系統動態特性的影響卻無從判斷，難于提出正確的改進方向。現在利用仿真可得出的實時數據，可以指導改進直到符合實用要求。這是因為經過幾十年的研究，液壓仿真軟件的性能已從原來的低精度、低速度，發展到高精度、高速度；從只能處理單輸入、單輸出的線性系統，發展到能處理多輸入、多輸出的非線性系統；從復雜的編程輸入，發展到友好的交互式圖形界面輸入。利用MATLAB對于液壓伺服系統進行仿真研究和計算機輔助分析，并從液壓仿真結論得出系統改進方向，不斷提高設備使用性能。

1 仿真分析的步驟

XYD小型液壓搗固機部分液壓系統的進行仿真分析的步驟如下［2］：

1）建立描述液壓系統特性的數學模型；

2）將數學模型轉化為適合計算機仿真的仿真模型；

3）選用適當的算法（一般為龍格-庫塔法）編制m文件；

4）通過計算機仿真，獲得液壓系統動態過程參數變化和響應特性的數據或曲線。

2 建立小液搗液壓特性數學模型

XYD小型液壓搗固機的液壓系統是主要工作系統之一，用以操縱和控制搗固機的主要工作部件。夾實裝置油缸內徑為65 mm，壁厚5 mm，雙行程，全行程為170 mm，活塞桿直徑為40 mm。每個油缸的工作推力為14.3 k N。因搗固桿懸掛在振動架上，其杠桿比為340/540即0.63，故在每對搗固掌上的壓力約為9.31 k N。根據夾實油缸伺服系統的原理（見圖1所示）及流體力學等理論基礎列寫基本方程［1］。

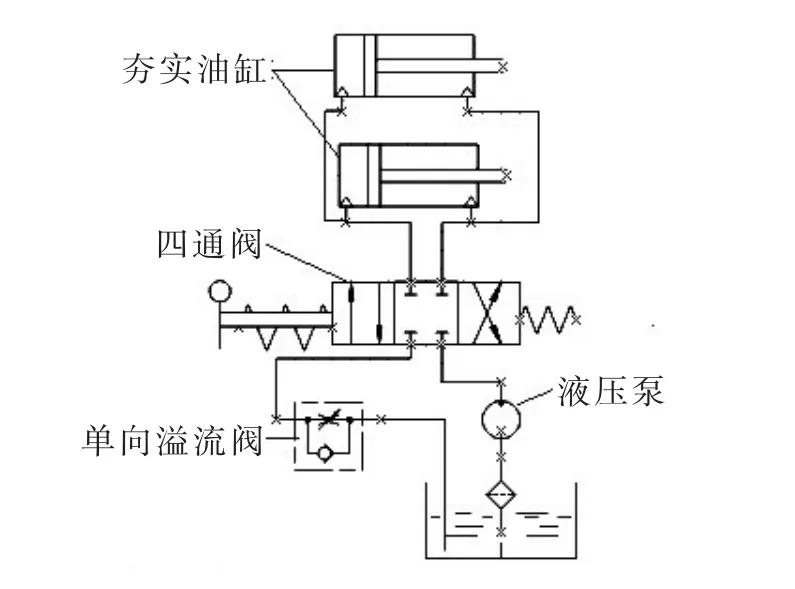
圖1 液壓原理圖

2.1 閥的線性化流量方程 為了推導液壓動力原件的傳遞函數，先要根據流體力學原理列寫出基本方程，再進行推到換算，首先根據總得進油口流量和泄漏量、出油口流量相等列寫出流量方程，又由于節流窗口對稱匹配，供油穩定，所以列寫出線性化流量方程式為

式中：Kc為四通閥的流量-壓力系數；

Kq為四通閥的流量增益；

pL為液壓缸有桿腔活塞上的壓力；

qL為四通閥的輸出流量；

xv為閥芯位移量。

由于外部泄漏和油液壓縮的影響，可取平均值作為負載流量。

2.2 液壓缸流量連續性方程 寫出線性化流量方程后，根據流體的連續性列寫第2個基本的流量的連續性方程，考慮到連接管路對稱、短粗，油溫、體積模數為常數，在實際中外泄漏量很小，可忽略不計。又因為閥是匹配和對稱的，所以通過閥節流口的流量也相等。可以寫出符合分析使用的流量連續性方程式為

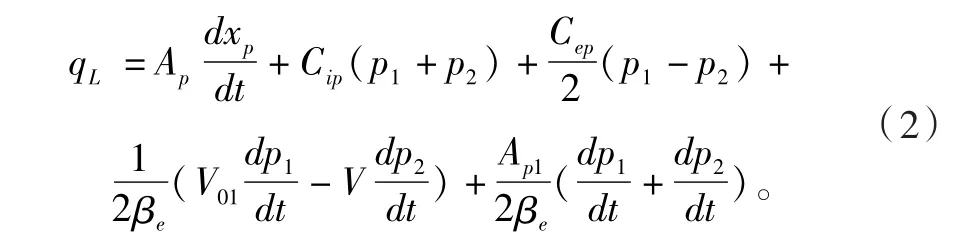
式中：Ap為活塞面積；

Cip為液壓缸的內泄漏系數；

xp為活塞位移；

Cep為液壓缸外泄漏系數；

V1、V2為液壓缸進油腔和回油腔體積；

βe為液體體積彈性系數；

V01、V02為液壓缸進油腔和回油腔的初始容積；

Vt為液壓缸進回油腔總體積。

活塞在中間位置時對液體壓縮影響最大，動力元件固有頻率最低，阻尼比最小。因此，系統穩定性最差。所以在分析時，應取活塞的中間位置為初始位置［2］。

2.3 液壓缸和負載的力平衡方程 由于負載特性影響液壓動力原件的動態特性，負載力一般包括慣性力、彈性力等。根據力的平衡原理列寫出第3個基本方程液壓缸和負載的力平衡方程式為

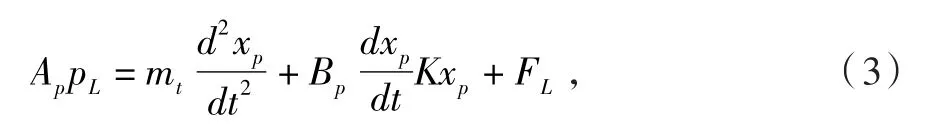
式中：mt為活塞與負載的總重量；

K為彈簧負載剛度；

Bp為活塞和負載折合到活塞上的總阻尼系數；

FL為負載干擾力。

此外，還存在一些非線性負載，但是采用線性化的方法分析系統的動態特性時，必須將線性負載忽略。式（1）、（2）、（3）是閥控液壓缸的基本方程，它們完全描述了閥控液壓缸的動態特性。3式的拉普拉斯變換式為

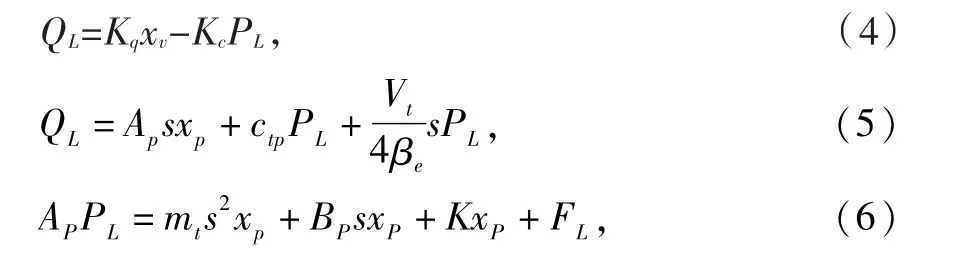
由式（4）、（5）、（6）消去中間變量，可以得到液壓缸活塞的中輸出位移為

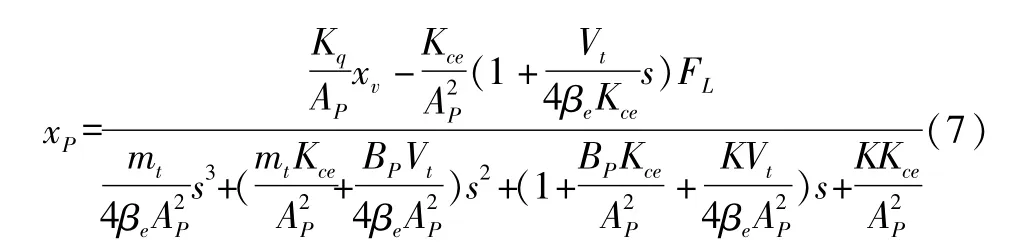
式中：Kce為總流量-壓力系數。

3 計算機仿真

3.1 建立計算機仿真模型 Matlab/Simulink軟件環境下對小型液壓搗固機的液壓夾實系統仿真是建立在數學模型的基礎之上，并根據實際情況進行合理簡化后進行計算機建模和仿真分析。式（7）中的閥芯位移xv是指令信號，外負載FL是干擾信號。由該式可以求出液壓缸活塞位移對閥芯位移的傳遞函數和對外負載力的傳遞函數。此式是一個考慮了多種因素的通用的形式，實際情況的負載往往比較簡單，可以根據具體情況忽略一些次要因素，簡化傳遞函數。需要描述和分析的情況是小型液壓搗固機夾實油缸伺服系統在夾實工況下的仿真，這種工況以慣性負載為主，而沒有彈性負載或者彈性負載極小可以忽略。另外粘性阻力系數一般也很小，所以其引起的泄露量所產生的活塞速度，比活塞運動速度小很多。因此可以忽略不計，即得簡化后傳遞函數為［2］

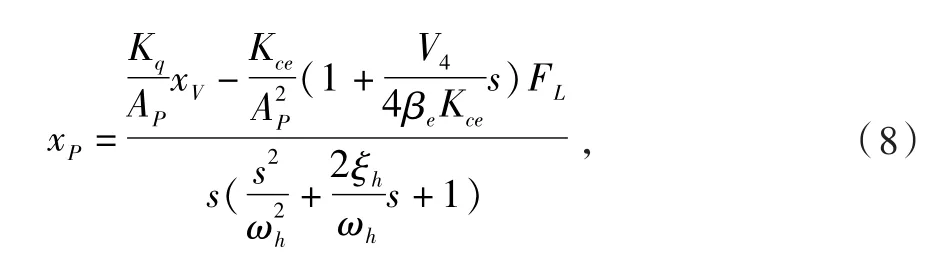
式中：ωh為液壓固有頻率

ξh為液壓阻尼比，BP一般很小

所以得對指令輸入的傳遞函數為

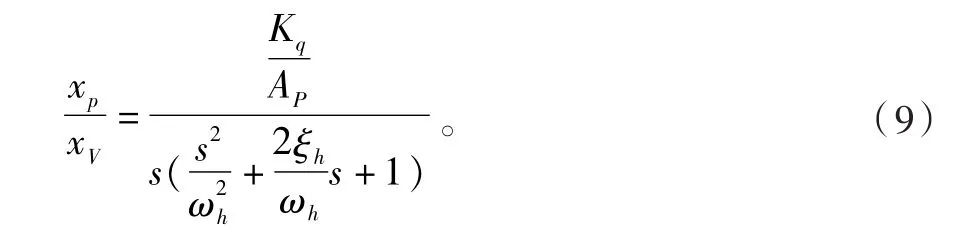
參考數據：mt=9.31 k N，B=10 N·s/n，Ap=0.005 m2，Kq=0.0726，βe=0.7×109Pa，Vt=0.008 4 m3

算得：ωh=0.79，ξh=0.08 即得

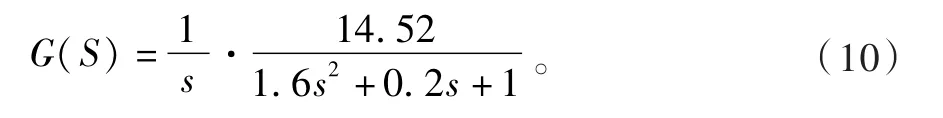
在結合實際工況分析后，做出了合理簡化得到傳遞函數式（10），并根據此式在仿真環境下進行仿真設計得到Matlab/Simulik軟件環境下的液壓夾實系統的系統仿真圖（見圖2），建立仿真模型后就可以開始對液壓系統進行動態仿真。

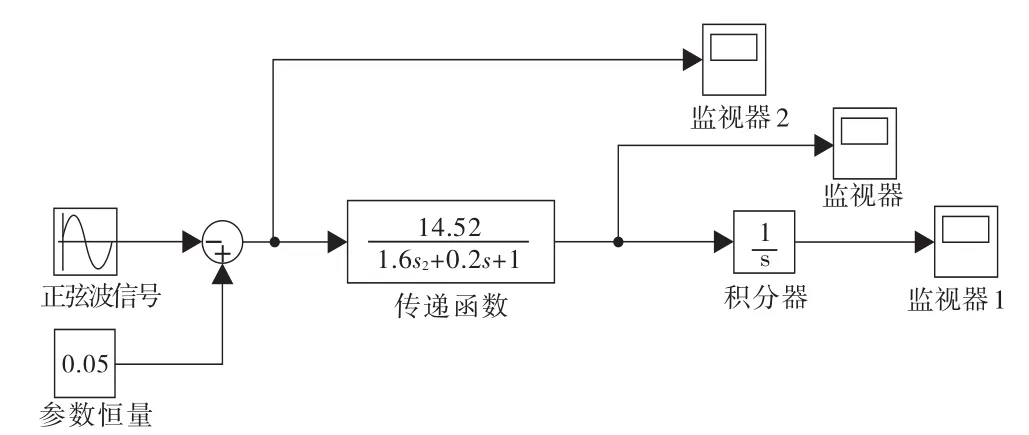
圖2 系統仿真圖

3.2 輸入信號 夾實液壓缸伺服系統主要是以往復運動為主，即活塞在液壓油的推動下伸出，然后又在液壓油的作用下活塞桿縮回的周期性工作。結合這個實際工況和便于觀察液壓缸在周期性工作下的動態特性，所以設定輸入信號為正弦信號，即在閥的初始開口流量為0.05 mm，閥的輸出位移呈正弦變化時，閥芯位移與時間的關系如圖3所示。仿真周期為4 s的條件下，進行仿真觀察液壓缸活塞輸出速度和輸出位移在時域內的響應曲線。

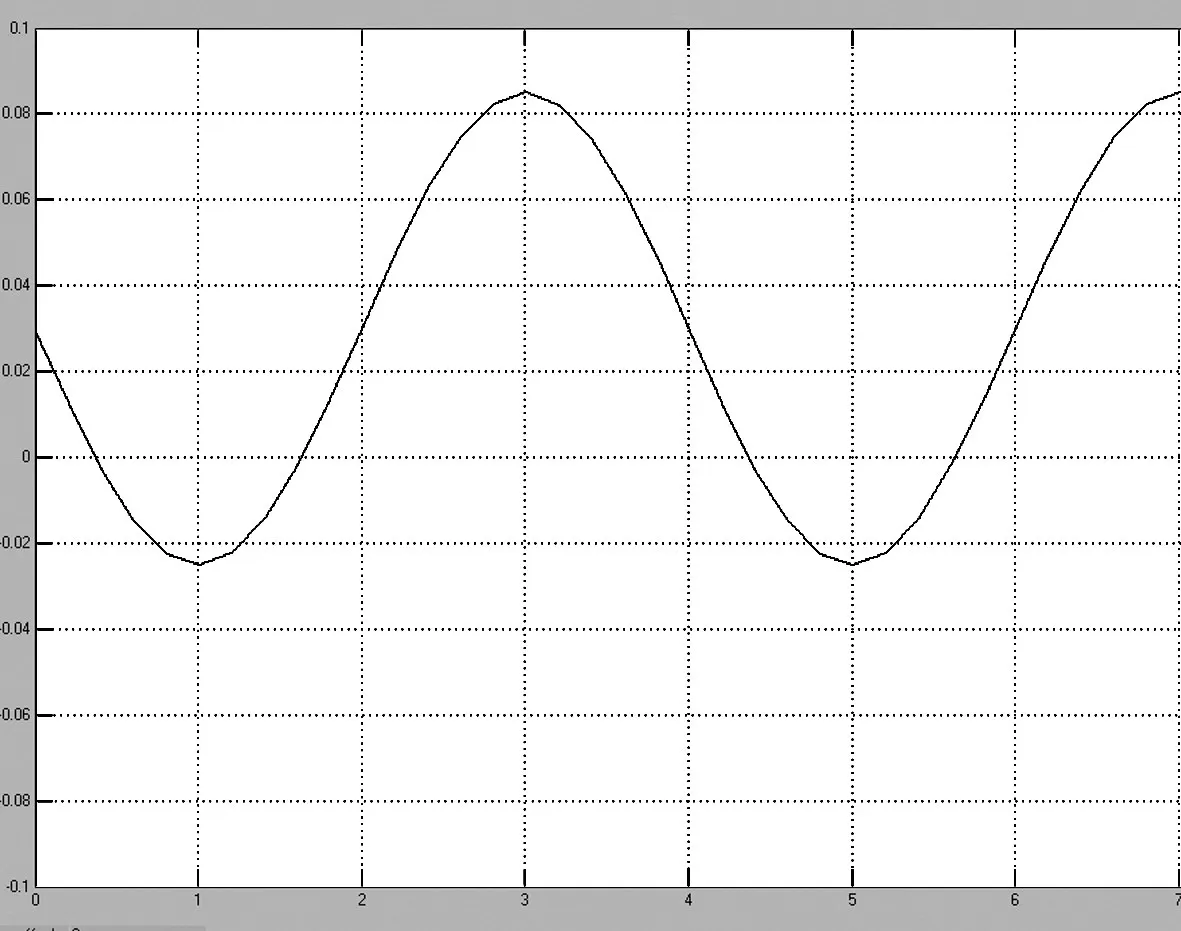
圖3 閥芯位移與時間關系

4 仿真結果分析

在設定好輸入信號和仿真相關參數后進行計算機仿真，動態仿真結果為輸出速度和輸出位移在時域內的響應曲線，分別如圖4、圖5所示。

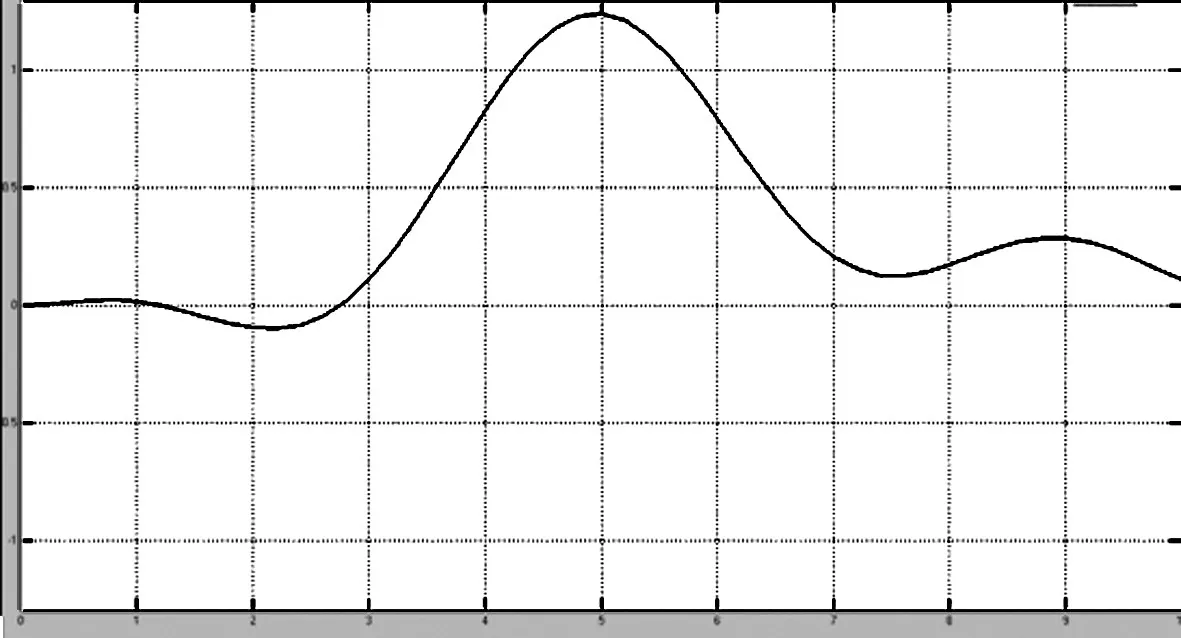
圖4 液壓缸活塞輸出速度v和時間t的關系

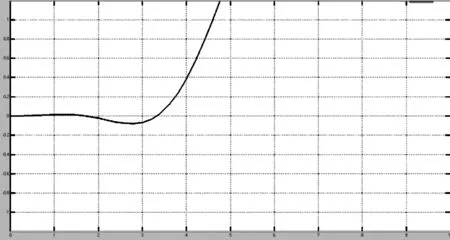
圖5 液壓缸活塞輸出位移y和時間t的關系

分析仿真結果，可以得出系統現有的不足，為改進系統提供明確的方向。

4.1 活塞速度在時域的響應曲線 從圖4的輸出量在時域的響應曲線可以了解系統的動態特性，活塞桿速度對輸入的響應近似正弦周期變化，這個響應是符合原理的。但是開始時響應不明顯，并有一段時間的延遲。同時速度變化不均勻，從圖上看有一個速度沖擊，可能會造成交的振動影響其他系統工作。通過圖上表現能得知系統是存在一定缺陷的，響應延遲和速度沖擊均會影響設備的使用效果。這就為進一步改進系統的性能提供的改進方向，可以從更換性能更好的液壓元件等方式來解決這些問題，提高設備性能。

4.2 活塞位移對時間的動態響應曲線 從圖5液壓缸的活塞輸出位移對時間的動態響應曲線分析，同樣位移響應也具有延遲，并且曲線有下降的趨勢。這說明接觸到負載以后，活塞桿在外力的作用下有縮回的現象，也就是說液體壓力不穩定。可能的原因是密封不嚴，有液壓油的泄露，這也是需要進一步改進的方面。同時，當負載質量降低以后，系統響應明顯變快，且沒有振蕩的過程，說明系統低負載質量情況下的動態特性要優于高負載質量時的動態特性。但在一般情況下，改變外負載的變化不大，當液體有效體積彈性模數βe提高以后，系統動態響應也明顯變快，且振蕩幅度很小，說明提高液體有效體積彈性模數，可以改善系統的動態特性。影響βe的因素很多，其中混入油中的空氣對βe影響最大。因此，要想提高系統的響應速度，應嚴格控制油中的空氣含量。在研究分析動態結果的基礎上，可以對系統進行目標明確的改進，改進后可以繼續仿真分析直到符合要求后再投入生產［4］。

5 結束語

運用MATLAB中SIMULINK軟件包可直接根據系統的數學模型來建立仿真模型，仿真模型是一種時域仿真，方便的觀察到系統變化的優勢，對小型液壓搗固機夾實系統進行了全過程仿真。通過對小型液壓搗固機夾實伺服系統的仿真結果的分析，分析得出結論為改進液壓缸提供明確的方向，并在以后的使用中可以根據動態特性結合實際使用的數據對夾實液壓伺服系統進行調整使之更好的滿足使用要求。同時運用仿真分析技術對小型液壓搗固機液壓系統其他子伺服系統進行仿真，得出合理的改進措施，最終優化整個小型液壓搗固機的液壓系統。

［1］鐵道部.鐵道科學研究院養路機械化研究室.XYD-1型小液壓搗固機［M］.北京：人民鐵道出版社，1978

［2］宋志安.基于MATLAB的液壓伺服控制系統分析與設計［M］.北京：國防工業出版社，2007.6

［3］林秋水.基于 Simulink的液壓控制系統的建模與仿真［J］.漳州師范學院學報（自然科學版），2006（3）：53-56.

［4］石紅雁，許純新，付連宇.基于SIMULINK的液壓系統動態仿真［J］.農業機械學報，2000（9）：96