協同系統魯棒波束成形算法研究
成文婧 徐玉清 劉兆和 王 欣
(1.總裝工程兵科研一所,江蘇 無錫214035 2.國防科學技術大學,湖南 長沙410073)
引 言
放大轉發(AF)協同波束成形系統,不僅實現簡單,而且通過波束成形技術可獲得協同分集[1-4]。該技術通過在各中繼節點處乘以預先設計的波束成形因子,使得目的節點處獲得較好的性能。與一般意義的波束成形問題[5]類似,該技術也是通過預先知道系統的一些信息來優化波束成形向量,以達到一定的優化目標(如目的節點信噪比(SNR)最大化、誤碼率最小化等)。波束成形系統要求中繼節點已知理想信道狀態信息(CSI),但是受信道估計誤差、量化誤差、反饋延遲等因素影響,實際一般不能獲得理想CSI。此時根據理想CSI設計的傳統波束成形算法性能嚴重下降。設計對不準確CSI具有魯棒性的波束成形算法是波束成形技術實用化的關鍵之一。
傳統波束成形設計準則一般有兩種:一是在保證目的節點SNR大于某門限的前提下,以最小化中繼節點總功率為準則;二是在中繼節點功率約束下,以最大化目的節點SNR為準則。不同準則下的波束成形,需要設計對應不同的魯棒算法。針對第一種準則,文獻[6-7]基于最壞情況思想,設計了對應魯棒算法。其中文獻[6]假設中繼節點得到的CSI僅在幅度上存在誤差,研究魯棒功率分配算法。文獻[7]進一步考慮CSI在幅度和相位上均存在誤差,設計了對應魯棒波束成形因子。針對第二種準則,文獻[8-9]也基于最壞情況思想,研究對應魯棒算法。但是文獻[8]僅考慮了第二階段(中繼到目的)CSI存在誤差,沒有考慮第一階段(源到中繼)信道誤差的影響。文獻[9]雖然考慮兩階段CSI信息都存在誤差,但是只考慮CSI幅度誤差,沒有考慮相位誤差。目前為止,針對獲得的兩階段CSI在幅度和相位上均存在誤差的情況,最大化目的節點SNR準則對應的魯棒波束成形算法還沒有進行研究。
針對所有中繼功率約束(TPC)下以最大化目的節點SNR為準則的協同波束成形系統,設計了對應的魯棒算法。具體來說,考慮中繼節點獲得的兩階段CSI存在復誤差,基于最壞情況思想,建立了對應保證魯棒性的優化問題。進而根據擴展S引理和復數矩陣Schur補定理,將此問題由不可解的半無限問題轉化為可解的準凸問題,可通過對分搜索算法獲得最優解。每次搜索可利用高效的內點算法來判斷聯合線性約束、二階錐(SOC)約束和線性矩陣不等式(LMI)約束的凸問題是否可解。仿真表明,提出的魯棒波束成形算法能夠有效抵抗不準確CSI帶來的性能損失。
符號表示:()·′、()·T、()·H分別表示取共軛、轉置和共軛轉置;表示a的模、∠a表示a的相位;⊙表示Hadamard乘積;diag{w}表示對角線元素為w的對角矩陣。
1 系統模型
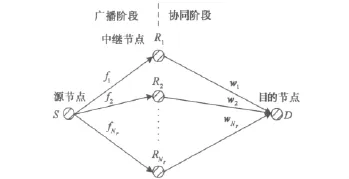
圖1 協同場景
考慮由源節點S、目的節點D和Nr個中繼節點Ri,i=1,…,Nr組成的協同系統,如圖1所示。各節點均配置半雙工的單天線。假設S和D間沒有直達路徑,由Nr個中繼節點協助S與D進行通信。令fi表示S到Ri的信道,wi表示Ri到D的信道,其中fi和wi服從均值為0、方差為1的復高斯分布。假設中繼節點對應各信道相互獨立,且各節點間達到理想同步。協同過程可分為兩個階段:
1)源節點以功率Ps將符號信息s發送給各中繼節點,且滿足E{|s|2}=1.則中繼節點Ri的接收信號為

式中ni表示Ri處的噪聲,服從均值為0,方差為1的復高斯分布。
2)Ri對接收信號ri乘以功率歸一化因子β=然后乘以波束成形因子g′i后發送至目的節點。則Ri的發送信號為
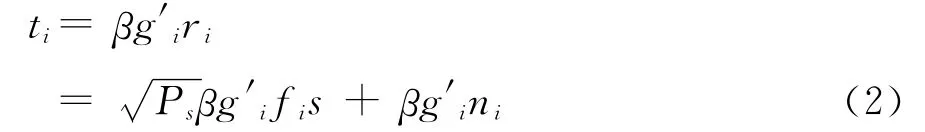

目的節點的接收信號為
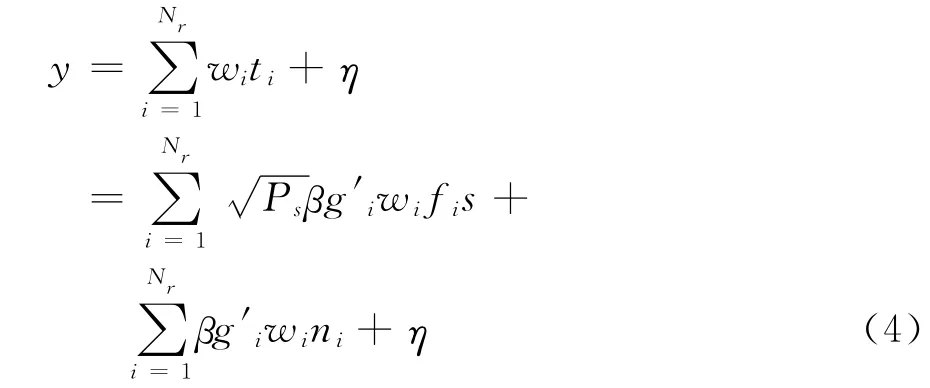
式中,η表示目的節點處的噪聲,服從均值為0,方差為1的復高斯分布。
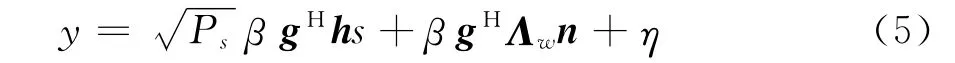
由式(5)可得,目的節點接收信號中的有效信號功率為Psig=Psβ2gHhhHg,噪聲功率為Pnoise=β2gHΛΛwg+1,則目的節點接收信號的SNR為
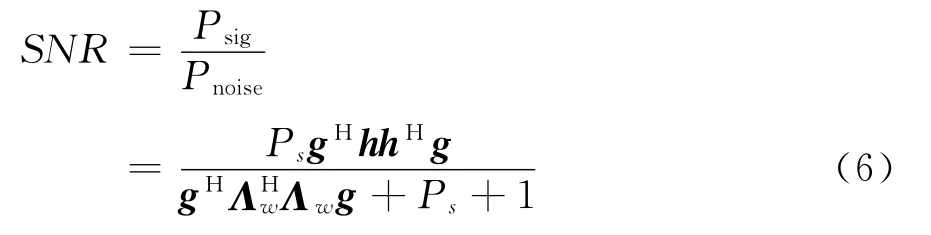
2 傳統波束成形設計
假設中繼節點的總功率不超過Pmax.由式(3)和式(6)可得,此波束成形設計問題可表示為
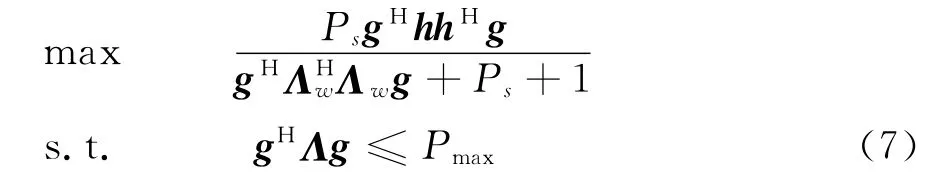
由文獻[11]可得,優化問題(7)的最優解為

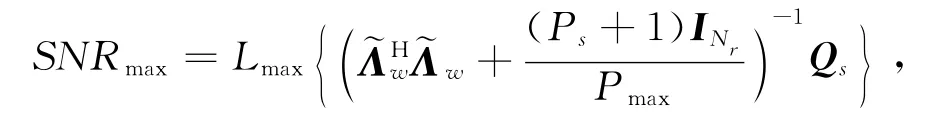
其中Lmax{·}表示矩陣的最大特征值。
3 最壞情況下的魯棒波束成形設計
實際系統中,節點很難獲得理想CSI.不準確CSI會嚴重影響傳統波束成形算法的性能。魯棒波束成形的目的是:合理設計波束成形矢量g,使得當節點得到的CSI存在誤差時,仍能獲得較好的性能。首先定義信道的不確定集,然后推導魯棒波束成形因子。
3.1 不確定集建模
假設實際信道向量是在中繼節點已知的信道向量上疊加一個復誤差向量。此時實際信道所有可能的取值構成信道不確定集,假設為橢圓不確定集:
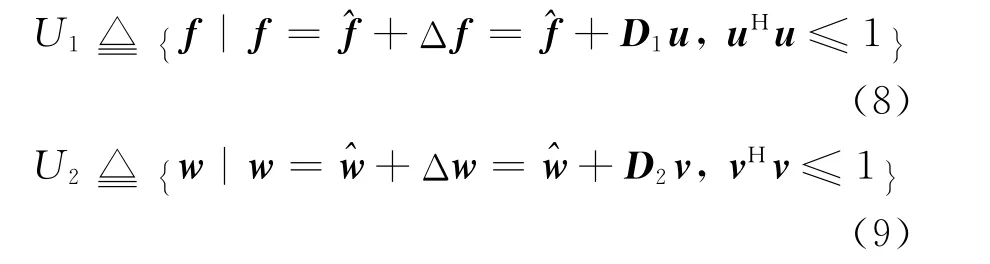
由式(8)可得Λf的不確定集為
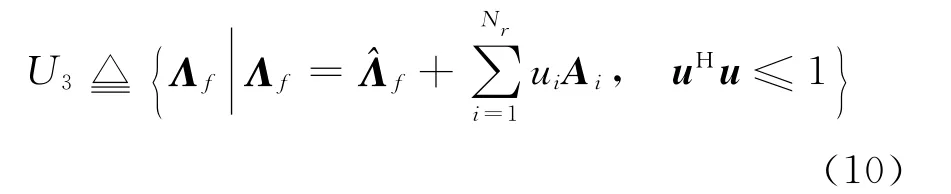
由式(9)可得Λw的不確定集為
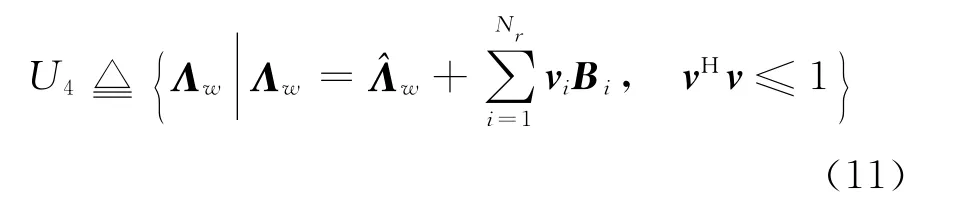
由式(8)和(9)可得
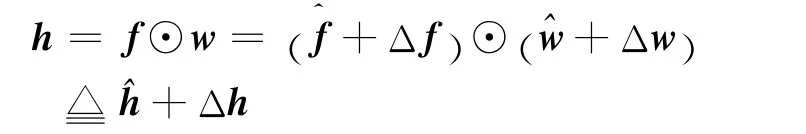
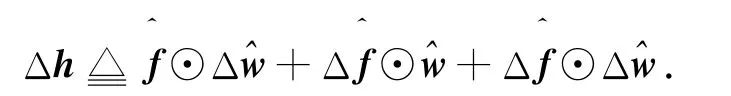
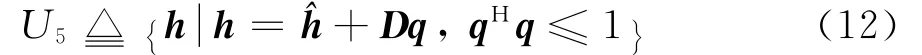
3.2 魯棒波束成形設計
由于信道的不確定性,TPC下的魯棒波束成形設計問題不能由第2節的方法得到解析解。
引入輔助變量α,優化問題(7)可等價為

則保證魯棒性的最優化問題可表示為
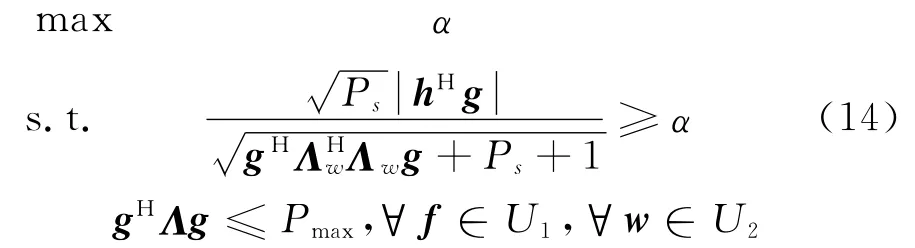
進一步等價為
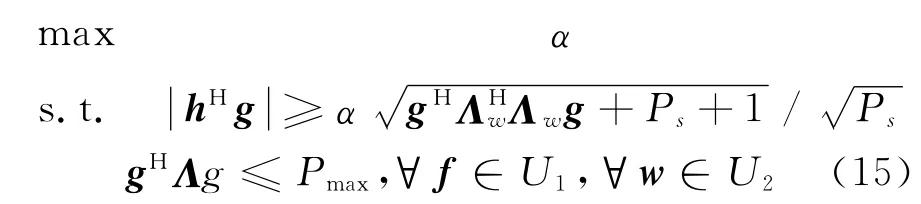
優化問題(15)的最優解即為最優魯棒波束成形因子。但是不確定集U1和U2中包含無窮個f和w,相當于優化問題(15)中包含無窮個約束條件,難以求解。實際上,要保證不確定集中任意信道都滿足約束條件,只要保證最壞情況下滿足條件即可。以下我們將基于最壞情況思想,建立新的約束條件,將優化問題(15)轉化為可解的凸問題。近似認為優化問題(15)的第一個約束條件的不等式兩邊涉及的不確定集是獨立的[6,9]。引入輔助變量τ≥0,優化問題(15)可等價為
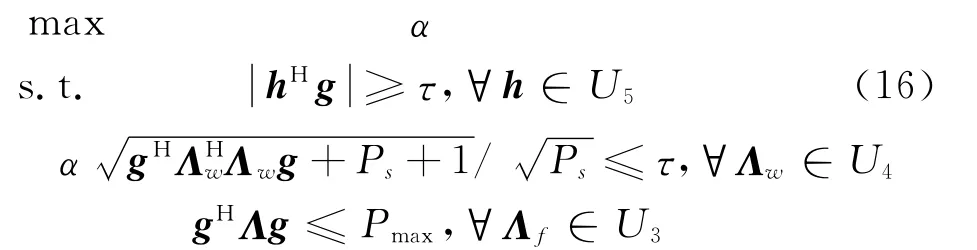
定理:優化問題(16)等價為可解的準凸問題(17)
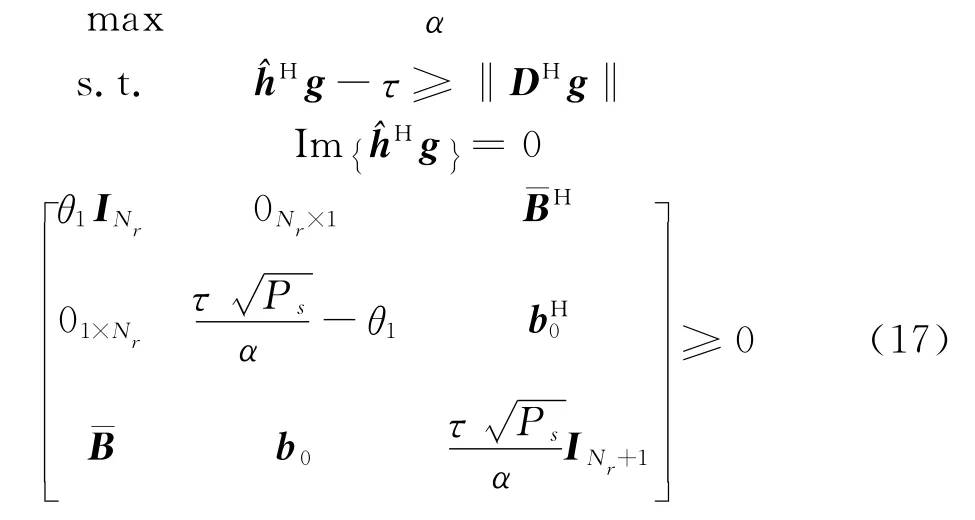
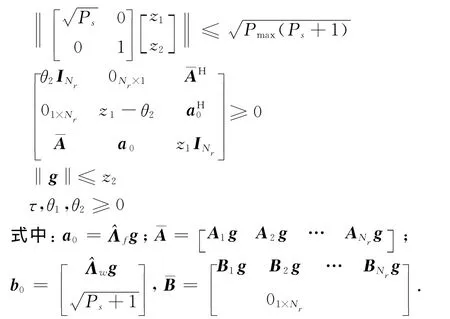
證明:
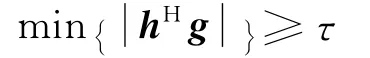
由于qHq≤1,根據Cauchy-Schwarz不等式可得
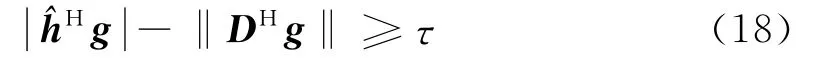
2)第二個約束條件等價為
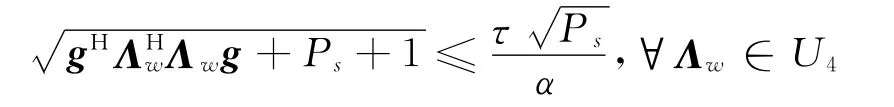
引入范數表示后可等價為
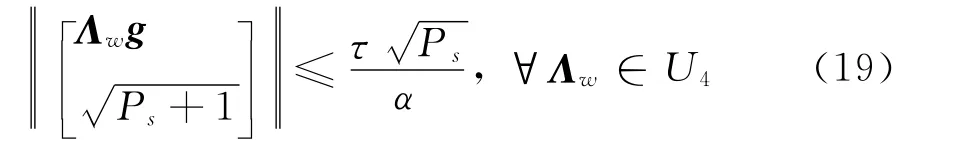
由式(11)可得
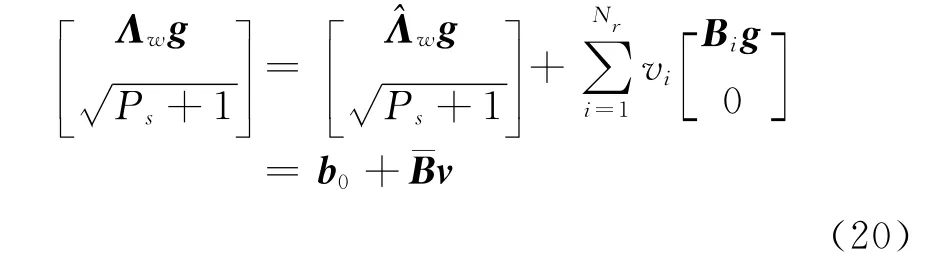
將式(20)代入式(19)中,并根據范數性質‖x‖2=xHx,式(19)可等價為
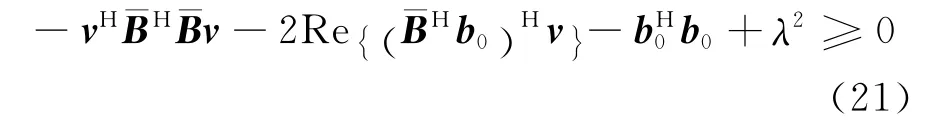
根據擴展S引理(附錄A),式(21)成立等價于:存在ρ1≥0,滿足
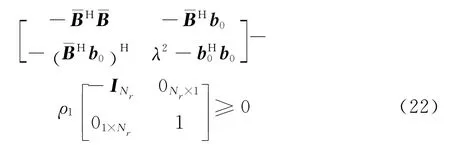
由于ρ1,λ均為非負數,所以一定存在θ1≥0,滿足ρ1=λθ1.則式(22)等價為
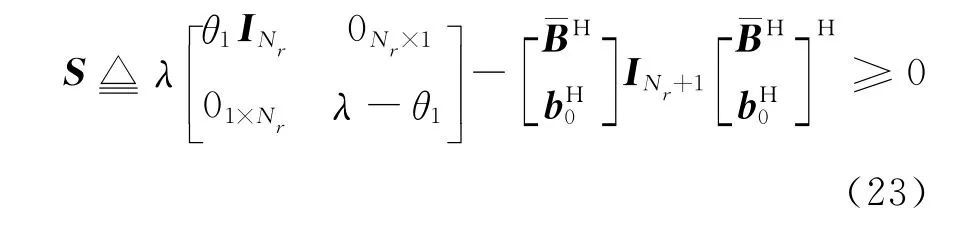
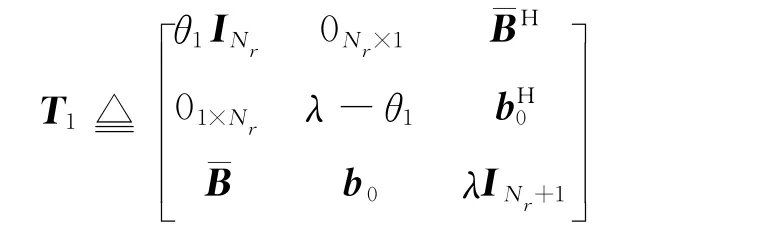
中的Schur補,根據復數矩陣的Schur補定理(見附錄B),S≥0等價于T1≥0.
因此第二個約束條件等價為

3)由式(3)可得,第三個約束條件gHΛg ≤Pmax,?Λf∈U3等價為
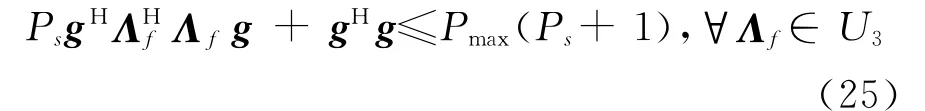
式(25)可等價為式(26)、(27)和(28)的聯合
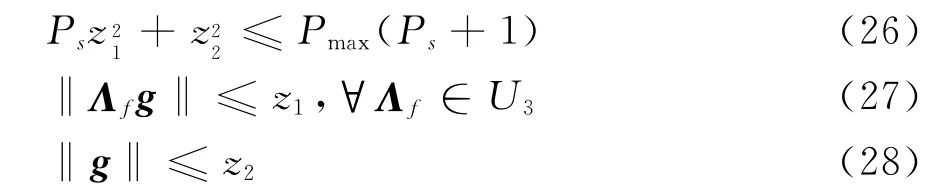
式(26)可以寫成二次型的形式,即
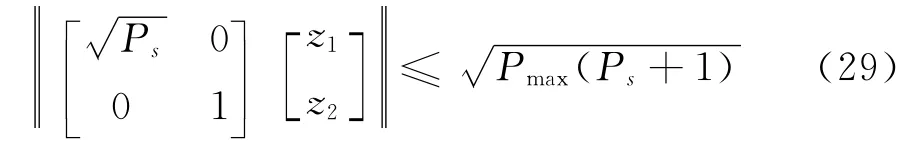
由于式(27)和(19)有著相似的結構,可通過類似的推導,得出式(27)的等價條件為
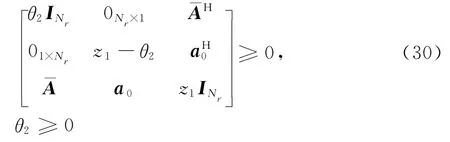
綜上所述,式(18),式(24),式(28),式(29)和式(30)為新的約束條件。
由于對g進行旋轉,不會影響優化問題(16)的目標函數,也不會影響新的約束條件,所以,可適當旋轉g,使得^hHg為實數。于是有優化問題(16)等價于式(17),定理得證。優化問題(17)的最優解即為最優魯棒波束成形矢量。該問題為準凸問題[12],可以通過對分搜索得到最優解。每次搜索需求解一個凸問題[13],包含4個線性約束,3個SOC約束和2個LMI約束。
4 仿真結果
仿真時取中繼數目Nr=5.為方便起見,取各中繼對應的兩階段信道的不準確程度一致,即δi=εi=δ,i=1,…,Nr.對分搜索時取ξ=1×10-6.
4.1 性能評價
當信道存在偏差時,非魯棒傳統算法設計的波束成形因子對應的節點功率可能大于功率約束。為公平比較算法性能,提出有效信噪比(ESNR)的概念。
定義中斷概率為ESNR小于門限γth的概率,即仿真中取γth=15dBw.
仿真過程如表1所示,取mon和time均為1 000.

表1 仿真過程
4.2 性能仿真
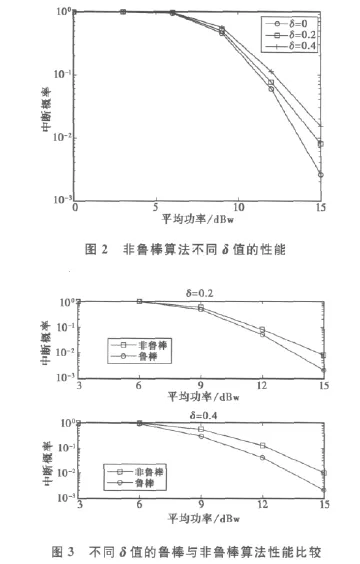
圖2為TPC下非魯棒傳統波束成形算法在不同δ值下的中斷概率性能曲線。可以看出,當δ=0.2時,CSI誤差對系統性能的影響不能忽略,而且隨著δ的增大,CSI誤差導致的性能損失更為嚴重。
圖3為δ=0.2和δ=0.4時,非魯棒傳統算法和提出的魯棒算法的性能比較,其中‘非魯棒’表示中繼節點已知的CSI存在誤差時,傳統波束成形算法根據有誤差的CSI設計的波束成形因子對應的性能,‘魯棒’表示中繼節點已知的CSI存在誤差時,提出的魯棒波束成形算法的性能。可以看出,提出的魯棒波束成形算法能夠有效改善CSI誤差對系統性能的惡化影響。
5 結 論
所提出的魯棒波束成形算法,可歸結為求解一個準凸問題,應用對分搜索可獲得最優解。每次搜索通過高效的內點算法來判斷聯合線性約束、SOC約束和LMI約束的凸問題是否可解。該算法能夠有效降低CSI偏差帶來的中斷概率性能損失,具有重要的實際意義。
[1]JING Y,JAFARKHANI H.Network beamforming using relays with perfect channel information[J].IEEE Transaction on Information Theory,2009,55(6):2499-2516.
[2]PHAM T,NGUYEN H,TUAN D.Beamforming in nonorthogonal amplify-and-forward relay networks[J].IEEE Transaction on Vehicular Technology,2011,60(3):1258-1263.
[3]CHENG W,HUANG Q,GHOGHO M,et al.Distributed beamforming for OFDM-based cooperative relay networks under total and per-relay power constraints[C]//IEEE ICASSP 2011.Prague,Czech Republic,22-27May,2011:3328-3331.
[4]CHEN H,GERSHMAN A,SHAHBAZPANAHI S.Filter-and-forward distributed beamforming in relay networks with frequency selective fading[J].IEEE Transaction Signal Processing,2010,58(3):1251-1262.
[5]李洪濤,賀亞鵬,朱曉華,等.基于譜分析的穩健自適應波束成形算法[J].電波科學學報,2012,27(1):147-151.LI Hongtao,HE Yapeng,ZHU Xiaohua,et al.Spectral analysis based robust adaptive beamforming algorithm[J].Chinese Journal of Radio Science,2012,27(1):147-151.(in Chinese)
[6]QUEK T Q S,SHIN H,WIN M Z.Robust wireless relay networks:slow power allocation with guaranteed QoS[J].IEEE Journal on Selected Topics in Signal Processing,2007,1(4):700-713.
[7]UBAIDULLA P,CHOCKALINGAM A.Robust distributed beamforming for wireless relay networks[C]//IEEE PIMRC 2009.Tokyo,Japan,September 13-16,2009:2345-2349.
[8]ZHENG G,WONG K K,PAULRAJ A,et al.Robust Collaborative-relay beamforming[J].IEEE Transaction on Signal Processing,2009,57(8):3130-3143.
[9]QUEK T Q S,WIN M Z,CHIANI M.Robust power allocation algorithms for wireless relay networks[J].IEEE Transaction on Communication,2010,58(7):1931-1938.
[10]VOROBYOV S A,GERSHMAN A B,LUO Z Q.Robust adaptive beamforming using worst-case performance optimization:A solution to the signal mismatch problem[J].IEEE Transaction Signal Processing,2003,51(2):313-324.
[11]SHAHBAZPANAHI S,GERSHMAN A B,LUO Z Q,et al.Robust adaptive beamforming for generalrank signal models[J].IEEE Transaction on Signal Processing,2003,51(9):2257-2269.
[12]BOYD S,VANDENBERGHE L.Convex Optimization[M].Cambridge:Cambridge University Press,2004.
[13]GRANT M,BOYD S.CVX:Matlab software for Disciplined Convex Programming[Online].http://stanford.edu/boyd/cvx
[14]LI J,STOICA P,WANG Z S.Doubly constrained robust capon beamformer[J].IEEE Transaction Signal Processing,2003,52(9):2407-2423.

